Хрестики-нулики
Хрестики-нулики (англ. tic-tac-toe) — гра на папері для двох гравців. На кожному ході гравці ставлять O чи X на ґратці розміром 3 на 3. Гравець, який першим розмістив три відповідних знаки в горизонтальному, вертикальному чи діагональному ряду, виграє партію.
 | |
| Тип гри | Ігри олівцем на папері |
|---|---|
| Кількість гравців | 2 |
| Час гри | ~1 хвилина |
| Вплив випадковості | відсутній |
Приклади: Цю партію виграв перший гравець, X:

Це партія в якій немає переможця — нічия:
Гравці скоро виявляють, що найкраща гра обох сторін обов'язково приводить до нічиєї. Тому у хрестики-нулики грають здебільшого діти.
Простота хрестиків-нуликів робить їх ідеальним педагогічним інструментом для навчання понять комбінаторної теорії ігор і відгалуження штучного інтелекту, що вивчає пошук в ігровому дереві. Дуже просто написати програму, що досконало грає в хрестики-нулики. Також можна перерахувати всі 765 принципово різних позицій (див. Складність гри) або 26 830 всіх можливих ігор з точністю до обертань та дзеркальних відображень.[1]
Гра може бути узагальнена до m,n,k-гри, в якій два гравці чергуються розміщуючи камені власного кольору на дошці розміром m×n, з метою отримання k штук власного кольору в ряд. Хрестики-нулики — це (3,3,3)-гра.[2] Френк Харарі зробив ще більше узагальнення гри. Вона може бути узагальнена як nd гра. Хрестики-нулики є грою, в якій n=3 та d=2.[3] Якщо грати правильно, то результатом буде нічия, що робить хрестики-нулики марною грою.[4]
Історія
В ранній варіант хрестиків-нуликів грали в Римській імперії, приблизно в першому столітті до нашої ери. Ця гра називалася Terni Lapilli (Терні Лапілі) та замість того, щоб мати будь-яку кількість знаків, у кожного гравця було всього три, таким чином, вони повинні були переміщувати їх у порожньому просторі, щоб продовжувати грати. Сітки з маркованною крейдяною грою були знайдені по всьому Риму. Однак, за словами Клаудії Заславської, за її книгою Tic Tac Toe: And Other Three-In-A Row Games from Ancient Egypt to the Modern Computer («Хрестики-нулики: та інші ігри три-в-ряд від стародавнього Єгипту до сучасного комп'ютера»), хрестики-нулики могли виникнути ще в Стародавньому Єгипті. Інша тісно пов'язана стародавня гра - Three Men's Morris, в яку також грали на простій сітці і, яка вимагає три знаки в ряд, щоб закінчити.
Різні назви гри з'явилися недавно. Перша згадка в пресі британської назви «Noughts and crosses» з'явилася в 1864 році. У своєму романі «Can You Forgive Her» Ентоні Троллоп вказує на клерка, який грає в «tit-tat-toe». Перша згадка в пресі гри під назвою «tick-tack-toe» з'явилася в 1884 році, але стосується «дитячої настільної гри, в яку грають на дошці, та яка полягає у спробах із закритими очима поставити олівець на одному з чисел набору; попадання зараховуються в очки». «Tic-tac-toe» можливо з'явилися від «tick-tack», старої версії назви гри в нарди, вперше згаданої в 1558 році. Перейменування Noughts and crosses на Tic-tac-toe в США сталася в 20 столітті.
У 1952 році, OXO (або Noughts and Crosses) для комп'ютера EDSAC стала однією з перших відомих відео ігор. Гравець може грати в хрестики-нулики проти людини.
У 1975 році, хрестики-нулики були також використані студентами MIT, щоб продемонструвати обчислювальну потужність елементів Лего. Комп'ютер Лего, зроблений з (майже) тільки Tinkertoys, вміє чудово грати в хрестики-нулики. Він в даний час експонується в Музеї науки в Бостоні.
Правила гри
Гравці по черзі ставлять на вільні клітини поля 3х3 знаки (один завжди хрестики, інший завжди нулики). Перший, хто зумів побудувати в ряд 3 своїх фігури по вертикалі, горизонталі або діагоналі, виграє. Перший хід робить гравець, що ставить хрестики.
Зазвичай по завершенні партії сторона, яка виграла закреслює рискою свої три знака (нулики або хрестика), які складають суцільний ряд.
Аналіз
Для кожної з сторін загальновідомі алгоритми, які гарантують нічию при будь-якій грі противника, а при його помилці дозволяють виграти. Таким чином, гра знаходиться в стані «нічийної смерті».
Нижче наведені деякі з таких стратегій. Вважається, що гравець завжди дотримується два правила, що мають пріоритет над усіма іншими:
- Правило 1. Якщо гравець може негайно виграти, він це робить.
- Правило 2. Якщо гравець не може негайно виграти, але його противник міг би негайно виграти, зробивши хід у якусь клітинку, гравець сам робить хід у цю клітинку, запобігаючи негайний програш.
За хрестики
Перший хід зробити в центр. Інші ходи, якщо незастосовні правила 1-2, робляться в той з вільних кутів, який найдалі від попереднього ходу нуликів, а якщо це неможливо — у будь-яку клітинку.
| Х | ||
Доведемо, що ця стратегія призводить до перемоги або нічиєї. Якщо нулик піде на сторону, то позиція (з точністю до симетрії) виявиться така:
| О | ||
|---|---|---|
| Х | ||
| Х |
Після чого правила 1 і 2 приведуть до позиції:
| Х | О | О |
|---|---|---|
| Х | ||
| Х |
Виграш.
Якщо ж нулик піде в кут, позиція (з точністю до симетрії) буде наступна:
| О | ||
|---|---|---|
| Х | ||
| Х |
В залежності від наступного ходу нулика, виникне одна з трьох позицій:
| О | О | Х |
|---|---|---|
| Х | ||
| Х |
| О | Х | О |
| Х | ||
| Х |
| О | ||
| Х | О | |
| Х | Х |
У першій і третій позиції — виграш. У другій — нічия.
За нулики
(Нагадуємо, що правила 1-2, якщо вони застосовні, мають пріоритет над усім, написаним нижче).
- Якщо хрестики зробили перший хід в центр, до кінця гри ходити в будь-який кут, а якщо це неможливо — у будь-яку клітинку.
| О | |
|---|---|
| Х |
- Якщо хрестики зробили перший хід в кут, відповісти ходом в центр.
| Х | |
|---|---|
| О |
- Наступним ходом зайняти кут, протилежний першому ходу хрестиків, а якщо це неможливо — піти на бік.
| Х | |
|---|---|
| О | |
| Х | О |
- Якщо хрестики зробили перший хід на бік, відповісти ходом в центр.
- Якщо наступний хід хрестиків — в кут, зайняти протилежний кут:
| Х | О | |
|---|---|---|
| О | ||
| Х |
- Якщо наступний хід хрестиків — на протилежну сторону, піти в будь-який кут:
| О | Х |
|---|---|
| О | |
| Х |
- Якщо наступний хід хрестиків — на сторону поряд з їх першим ходом, піти в кут поруч з обома хрестиками
| О | Х |
| Х | О |
Дерево ігрових ситуацій
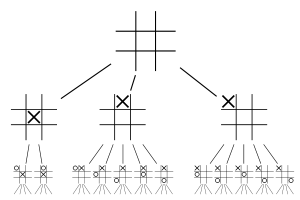
Дерево ігрових ситуацій для гри хрестики-нулики, де гравець за «хрестики» ходить першим і діє за наведеним вище алгоритмом, а гравець за «нулики» може чинити як завгодно (причому наведено по одній вершині для раціонального і для нераціонального вчинку, тобто будь-якого іншого), складається з 50-ти вузлів
Комп'ютерний розв'язок
Для вирішення такого роду ігор на комп'ютері будується дерево ігрових ситуацій у відповідності з методом міні-макс. Повне число вузлів в такому дереві одно 255168. Це число виходить як сума всіх можливих варіантів ходів — 9 варіантів на першому кроці, 8 — для кожного з 9 на другому кроці, 7 — на кожному з 72 варіантів на третьому кроці і т. д., за винятком ситуацій дострокового закінчення гри (виграшу).
Більш довгі лінії
Можна розглядати гру, в якій переможцем вважається гравець, який першим побудував n ≥3 однакових знаків на досить великому для цього прямокутному полі. При цьому можна обмежити поле яким-небудь розміром (починаючи з n×n), або зовсім не обмежувати (в цьому випадку говорять про «нескінченне» поле).
Гра до 4 однакових знаків на нескінченному полі нецікава, бо початківець досить швидко будує «вилку» і виграє. Гра за n ≥6 також нецікава через «нічийну смерть». Існують стратегії, що не дають противнику побудувати потрібну лінію ніколи. Однак при n=5 гра стає набагато змістовнішою. Такий варіант має спеціальну назву — гомоку. Спочатку в гомоку грали на дошці розміром 19×19, пізніше вона була зменшена до розміру 15×15 клітин.
Основною переможною тактикою при грі на нескінченному полі вважається побудова перетинів («вилок»), які не дають противнику можливості блокувати всі можливі шляхи побудови п'ятірки. Щоб не програти, необхідно своєчасно переривати лінії противника довжиною в три фігури і більше.
Практика показала, що при рівних правила для гравців той, хто робить перший хід, має перевагу, що дозволяє при досить кваліфікованій грі здобути перемогу, що згодом було доведено суворо. Для збереження інтересу до гри пропонувалися різні варіанти модифікації правил гри. Так, з введенням фолів (заборонених ходів) для гравця, що починає першим — йому заборонено будувати вилки 3×3, 4×4, а також вибудовувати «довгий ряд» з своїх фігур — вийшла нова гра під назвою рендзю, з великою різноманітністю стратегій гри і рівними шансами гравців.
Модифікація поля
Збільшення розміру поля вже обговорювалося вище. Самим простим, але таким, що збільшує тактичне багатство гри, є додавання однієї клітини вздовж однієї із сторін поля 3х3.
Іншим варіантом є зміна топології поля. Наприклад, можна вважати протилежні сторони поля склеєними, утворюючи при цьому поверхню циліндра або тора, або проективну площину. Також можна збільшувати розмірність, наприклад, грати в кубі 4x4x4, в гіперкубі і так далі.
Можливий алгоритм для гри хрестики-нулики в кубі 4x4x4:
1. Перевіряємо наявність своїх трьох фігур, які стоять поспіль, якщо знайшли, то ставимо четверту (гра завершується).
2. Перевіряємо наявність трьох фігур супротивника, які стоять поспіль, якщо знайшли, то ставимо свою четверту.
3. Перевіряємо наявність своїх двох фігур, які стоять поспіль, якщо знайшли, то ставимо на будь-яку третю позицію в цьому ряду.
4. Перевіряємо наявність двох фігур супротивника, які стоять поспіль, якщо знайшли, то ставимо третю свою на будь-яку позицію в цьому ряду.
5. Шукаємо будь-який ряд, що має три порожні клітинки і містить одну свою фігуру і ставимо на будь-яку позицію в цьому ряду свою фігуру, причому перевага віддається наявності ряду в просторі.
Обмін значків
Можна скасувати правило, яке вказує гравцям ставити тільки свій вигляд значків. Наприклад, варіантом гри може бути: гравці ставлять хрестик або нулик (що захочуть), перший виграє, якщо хто-небудь побудує лінію потрібної довжини з однакових значків, другий — якщо до заповнення поля цього не станеться.
Зміна умов виграшу
Замість того, щоб закінчувати гру побудовою першої лінії потрібної довжини, можна на цьому не зупинятися і продовжувати до повного заповнення поля. Наприклад, на будь-якому полі можна грати на те, хто більше побудує «четвірок» зі своїх знаків.
Також існує варіант хрестиків-нуликів Силвермена. У ньому використовується ігрове поле 4х4 клітини. Хрестики виграють, якщо виникає ряд з 4-х однакових значків (хрестиків або нуликів), інакше виграють нулики.
Подовження ходу
Ще один варіант модифікації гри — виставляти на кожному ході не один свій знак, а два або більше. Така гра Connect6, в якій чорні роблять перший хід, виставляючи один знак, після чого гравці по черзі виставляють по два знаки, перемагає перший, хто побудував лінію з 6 або більше своїх знаків.
Див. також
Примітки і посилання
- Schaefer, Steve (2002). MathRec Solutions (Tic-Tac-Toe). Процитовано 18 вересня 2015.
- Pham, Duc-Nghia; Park, Seong-Bae (12 листопада 2014). PRICAI 2014: Trends in Artificial Intelligence: 13th Pacific Rim International Conference on Artificial Intelligence, PRICAI 2014, Gold Coast, QLD, Australia, December 1-5, 2014, Proceedings (англ.). Springer. ISBN 9783319135601.
- Golomb, Solomon; Hales, Alfred. Hypercube Tic-Tac-Toe. Процитовано 17 грудня 2016.
- W., Weisstein, Eric. Tic-Tac-Toe. mathworld.wolfram.com (англ.). Процитовано 12 травня 2017.
Література
- Гарднер М. Крестики-нолики. -М.:Мир, 1988. ISBN 5-03-001234-6.
