Циліндр

Цилі́ндр (грец. κύλινδρος — «валик») — геометричне тіло, обмежене замкнутою циліндричною поверхнею і двома паралельними площинами, що перетинають її.

Прямий круговий циліндр. h — вісь циліндра; r — радіус.

Види циліндрів

Нескінченний циліндр — це нескінченне тіло, обмежене замкнутою нескінченною циліндричною поверхнею.

Відкритий циліндр — обмежене замкнутим циліндровим променем і його основою геометричне тіло.

Основи циліндра якісно впливають на циліндр:

якщо основи циліндра пласкі (отже, що містять їх площині рівнобіжні) — циліндр називають таким, що стоїть на площині;
якщо основи стоять на площині циліндра перпендикулярні твірним — прямий циліндр; зокрема, якщо основа що стоїть на площині циліндра:
- коло — круглий циліндр;
- еліпс — еліптичний циліндр.

Елементи циліндра

Круги, що утворюють циліндр називаються основами циліндра. Вони рівні і лежать у паралельних площинах.

Твірні циліндра — відрізки, що сполучають відповідні точки кіл кругів. Вони паралельні і рівні між собою.

Поверхня циліндра складається з основ і бічної поверхні.

Бічна поверхня складається з твірних.

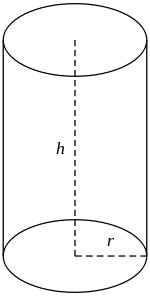
Радіусом циліндра називається радіус його основи.

Висотою циліндра називається відстань між площинами основ.

Віссю циліндра називається пряма, яка проходить через центри основ. Вона паралельна твірним.

Осьовий переріз — переріз циліндра площиною, яка проходить через вісь циліндра. Осьовий переріз є прямокутником, сторони якого — діаметр та твірна циліндра[1].

Дотична до циліндра — площина, яка проходить через твірну прямого циліндра і перпендикулярна до осьового перерізу, проведеного через цю твірну, називається площиною.

Циліндр називається прямим, якщо його твірні перпендикулярні до площин основ. Прямий циліндр можна розглядати як тіло, утворене обертанням прямокутника навколо його сторони як осі.

Площа поверхні

Площа бічної поверхні

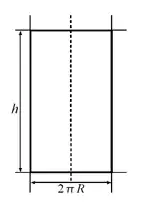
Площа бічної поверхні тіл обертання обчислюється за їхньою розгорткою. Розгортка циліндра являє собою прямокутник з висотою $h$ і довжиною $2\pi R$ , отже площа бічної поверхні циліндра дорівнює площі його розгортки та обчислюється за формулою:

$S_{b}=2\pi Rh$

Площа загальна

Площа повної поверхні циліндра дорівнює сумі площ його бічної поверхні та його основ:

$S_{p}=2\pi R(h+R)$

Об'єм

Візьмемо плоску фігуру, утворену такими прямими: y = R, x = 0, x = h, y = 0 та будемо обертати її навколо осі Ox. Таким чином ми отримуємо тіло обертання, утворене обертанням прямокутника навколо однієї з його сторін, тобто циліндр.

$V=\pi \int \limits _{0}^{h}R^{2}dx=\pi {\Bigl .}R^{2}x{\Bigr |}_{0}^{h}=\pi R^{2}h$ ,

кінцева формула:

$V=\pi R^{2}h=\pi {\frac {d^{2}}{4}}h$ ,

де d — діаметр основи; R — радіус основи.

Див. також

Примітки

Апостолова Г. В. Геометрія: 11 кл.: підруч. для загальноосвіт. навч. закл.:академ. рівень, профіл. рівень / Г. В. Апостолова; упорядкув. завдань: Ліпчевського Л. В. [та ін.]. - К.: Генеза, 2011. - 304 с.: іл. – С. 155 ISBN 978-966-11-0065-6.

Джерела

Корн Г. А., Корн Т. М. Справочник по математике для научных работников и инженеров. — 4-е. — М.: Наука, 1978. — 277 с.
Геометрія. 10-11 класи [Текст] : пробний підручник / Афанасьєва О. М. [та ін.]. — Тернопіль: Навчальна книга-Богдан, 2003. — 264 с. — ISBN 966-692-161-8

Посилання

Циліндр; Твірна // Універсальний словник-енциклопедія. — 4-те вид. — К. : Тека, 2006.
Циліндр // Термінологічний словник-довідник з будівництва та архітектури / Р. А. Шмиг, В. М. Боярчук, І. М. Добрянський, В. М. Барабаш ; за заг. ред. Р. А. Шмига. — Львів, 2010. — С. 209. — ISBN 978-966-7407-83-4.

Перерізи циліндрів. (англ.)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Апостолова Г. В. Геометрія: 11 кл.: підруч. для загальноосвіт. навч. закл.:академ. рівень, профіл. рівень / Г. В. Апостолова; упорядкув. завдань: Ліпчевського Л. В. [та ін.]. - К.: Генеза, 2011. - 304 с.: іл. – С. 155 ISBN 978-966-11-0065-6.