Циклічний код
Циклічний код — лінійний код, що володіє властивістю циклічності, тобто кожна циклічна перестановка кодового слова також є кодовим словом. Використовується для перетворення інформації, для захисту її від помилок (див. Виявлення і виправлення помилок).
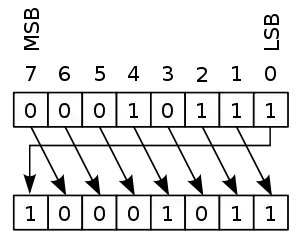
Введення
Нехай — слово довжини n над алфавітом з елементів кінцевого поля та — поліном, що відповідає цьому слову, від формальної змінної . Видно, що ця відповідність не просто взаємно однозначна, а й ізоморфна. Оскільки «слова» складаються з літер з поля, то їх можна складати та множити (поелементно), причому результат буде в тому ж полі. Поліном, що відповідає лінійній комбінації пари слів та , дорівнює лінійній комбінації поліномів цих слів .
Це дозволяє розглядати множину слів довжини n над кінцевим полем як лінійний простір поліномів зі ступенем не більше n-1 над полем .
Алгебраїчний опис
Якщо — кодове слово, що виходить циклічним зрушенням на один розряд вліво зі слова , то відповідний йому поліном виходить з попереднього множенням на x:
, користуючись тим, що ,
Зрушення вправо та вліво відповідно на розрядів:
Якщо — довільний поліном над полем та — кодове слово циклічного коду, то теж кодове слово цього коду.
Породжуючий поліном
Визначення: породжуючим поліномом циклічного коду називається такий ненульовий поліном з , ступінь якого найменша та коефіцієнт при старшому ступені .
Теорема 1
Якщо — циклічний код і — його породжуючий поліном, тоді ступінь дорівнює та кожне кодове слово може бути єдиним чином представлено у вигляді
,
де ступінь менше або дорівнює .
Теорема 2
— породжуючий поліном циклічного коду є дільником двочлена
Наслідки: таким чином як породжуючий поліном можна вибирати будь-який поліном, дільник . Ступінь обраного полінома визначатиме кількість перевірочних символів , число інформаційних символів .
Породжуюча матриця
Поліноми лінійно незалежні, інакше при ненульовому , що неможливо.
Значить кодові слова можна записувати, як і для лінійних кодів, таким чином:
, де є породжуючою матрицею, — інформаційним поліномом.
Матрицю можна записати в символьній формі:
Перевірочна матриця
Для кожного кодового слова циклічного коду справедливо . Тому перевірочну матрицю можна записати як:
Тоді:
Кодування
Несистематичне
При несистематичному кодуванні кодове слово виходить у вигляді добутку інформаційного полінома на породжуючий
.
Воно може бути реалізовано за допомогою перемноження поліномів.
Систематичне
При систематичному кодуванні кодове слово формується у вигляді інформаційного подблока та перевірочного
Нехай інформаційне слово утворює старші ступені кодового слова, тоді
Тоді з умови , слід
Це рівняння задає правило систематичного кодування. Воно може бути реалізовано за допомогою багатотактних лінійних фільтрів(БЛФ).
Приклади
Бінарний (7,4,3) код
Як дільник виберемо породжуючий поліном третього ступеня , тоді отриманий код буде мати довжину , число перевірочних символів (ступінь породжуючого полінома) , число інформаційних символів , мінімальна відстань .
Породжуюча матриця коду:
,
де перший рядок є записом полінома коефіцієнтами по зростанню ступеня. Решта рядків — циклічні зрушення першого рядка.
Перевірочна матриця:
,
де i-ий стовпець, починаючи з 1-го, являє собою залишок від ділення на поліном , записаний за зростанням ступенів, починаючи зверху.
Так, наприклад, 4-й стовпець виходить , або у векторному записі .
Легко переконатися, що .
Бінарний (15,7,5) БЧХ-код
Як породжуючий поліном можна вибрати добуток двох дільників :
.
Тоді кожне кодове слово можна отримати за допомогою добутку інформаційного полінома зі ступенем таким чином:
.
Наприклад, інформаційному слову відповідає поліном , тоді кодове слово , або у векторному вигляді
