Циліндрична система координат

Циліндрична система координат — тривимірна система координат, кожна точка якої задається двома полярними координатами на перпендикулярній проєкції деякої фіксованої площини та відстанню (зі знаком) від цієї площини.



Циліндрична система координат з початком в O, полярною віссю А, вертикальною віссю L. Позначена точка має координати з радіальною відстанню ρ = 4, кутовою координатою φ = 130 °, і висотою Z = 4.

Полярні координати можна назвати радіальною відстанню або радіусом і кутом або азимутом, відповідно. Третю координату можна назвати висотою (якщо площина відліку горизонтальна).[1] Лінію, перпендикулярну до площини відліку, яка проходить через центр координат можна назвати циліндричною віссю.

Циліндричні координати корисні в зв'язку з об'єктами і явищами, які мають деяку обертальну симетрію відносно циліндричної осі, такі, як потік води в прямій трубі з перетином у вигляді кола, розподіл тепла в металевому циліндрі, і так далі.

Визначення

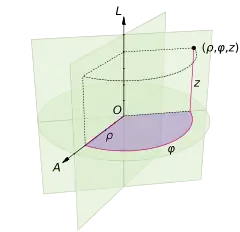
Три координати (ρ, φ, z) точки Р визначають як:

  • Радіальна відстань ρ евклідова відстань від осі до точки P.
  • Азимут φ — це кут між напрямом відліку на вибраній площині, та променем, що проходить з точки початку координат до проєкції P на площині.
  • Висота Z дорівнює відстані від обраної площини до точки P.

Унікальні циліндричні координати

Як і в полярних координатах, одна й та сама точка (ρ, φ, z) може мати нескіченну кількість еквівалентних циліндричних координат: (ρ, φ ± n×360°, z) та (−ρ, φ ± (2n + 1)×180°, z) де N — довільне ціле число. Крім того, якщо радіус ρ дорівнює нулю, то азимут може бути довільним.

У ситуаціях, коли потрібен унікальний набір координат, слід накласти такі обмеження: радіус має бути невід'ємним (ρ ≥ 0), азимут φ бути в інтервалі, що покриває 360°, наприклад (-180°, 180°] або [0, 360°).

Посилання
  1. C. Krafft, A. S. Volokitin (2002), Resonant electron beam interaction with several lower hybrid waves. Physics of Plasmas, volume 9, issue 6, 2786—2797. DOI:10.1063/1.1465420 «…in cylindrical coordinates (r,θ,z) … and Z=vbzt is the longitudinal position…».

Див. також
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.