Цисоїда Діокла

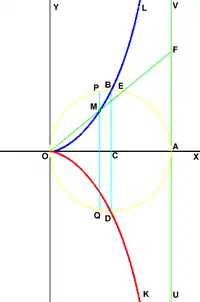
Цисоїда Діокла — плоска алгебрична крива третього порядку. В декартовій системі координат, де вісь абсцис спрямована за $OX$ , а вісь ординат за $OY$ на відрізку $OA=2a$ , як на діаметрі будується допоміжне коло. В точці $A$ проводиться дотична $UV$ . З точки $O$ проводиться довільна пряма $OF$ , яка перетинає коло в точці $E$ і дотичну в точці $F$ . Від точки $F$ у напрямку точки $O$ , відкладається відрізок $FM$ , довжина якого дорівнює довжині відрізка $OE$ . При обертанні лінії $OF$ навколо точки $O$ , точка $M$ описує лінію, яка називається цисоїда Діокла. Дві гілки цієї лінії на мал. 1 показані синім і червоним кольорами.

Мал. 1. Побудова цисоїди. Синя і червона лінії — гілки цисоїди.

Рівняння

Рівняння цисоїди в прямокутній системі координат записується так:

y^{2}={\frac {x^{3}}{2a-x}}.\qquad \qquad (1)

Рівняння цисоїди в полярній системі координат:

\rho ={\frac {2a\sin ^{2}\varphi }{\cos \varphi }}.

Іноді рівняння цисоїди в полярній системі координат записують так:

\rho ={\frac {2a\left(1-\cos ^{2}\varphi \right)}{\cos \varphi }}=

=2a\left({\frac {1}{\cos \varphi }}-\cos \varphi \right)=

=2a\left(\sec \varphi -\cos \varphi \right).

Параметричне рівняння цисоїди:

x={\frac {2au^{2}}{1+u^{2}}},

y={\frac {2au^{3}}{1+u^{2}}},

де

u=\mathrm {tg} \,\varphi

.

Історія

Вперше цисоїду досліджував грецький математик Діокл у II столітті до н. е. Діокл будував криву так: знаходиться точка $P$ , розташована на допоміжному колі симетрично точці $E$ ; вісь симетрії — діаметр $BD$ . З точки $P$ проводиться перпендикуляр до осі абсцис. Точка $M$ , що належить цисоїді, знаходиться на перетині цього перпендикуляра і прямої $OE$ . Цим методом Діокл побудував тільки криву $DOB$ всередині допоміжного кола. Якщо цю частину цисоїди ( $DOB$ ) замкнути дугою кола $EAD$ , то виходить фігура, що нагадує своєю формою листок плюща. Грецькою плющ — χισσος («хіссос»), від чого й походить назва кривої — «цисоїда».

В сучасному вигляді цисоїду відтворив французький математик Жиль Роберваль у 1640 році. Пізніше цисоїду також досліджував голландський математик Слюз.

Властивості

Цисоїда симетрична відносно осі абсцис.
Цисоїда перетинає допоміжне коло в точках $B$ і $D$ , які належать діаметру цього кола.
Цисоїда має один касп і асимптоту $UV$ , рівняння якої: $x=2a$ , де $a$ — радіус допоміжного кола.
Цисоїда є евольвентою параболи з каспом у вершині параболи. При цьому директриса параболи є асимптотою цисоїди.[1]

Площа між цисоїдою і асимптотою

Ця площа дорівнює:

S_{1}=3\pi a^{2}.

Виведення

Площа, охоплена гілками цисоїди $KOL$ і асимптотою $UV$ $S_{1}$ . Рівняння верхньої гілки $OL$ :

y={\sqrt {\frac {x^{3}}{2a-x}}}.\qquad \qquad (2)

Половина площі, укладеної між цисоїдою і асимптотою, дорівнює інтегралу від рівняння (2) в межах від 0 до $2a$ :

{\frac {1}{2}}S_{1}=\int \limits _{0}^{2a}{\sqrt {\frac {x^{3}}{2a-x}}}\,dx.\qquad \qquad (3)

Підстановка:

u^{2}=2a-x,\qquad x=2a-u^{2},\qquad dx=-2u\,du.

Межі інтегрування:

x=0\Rightarrow u={\sqrt {2a}},\qquad x=2a\Rightarrow u=0.

Інтеграл (3) перетворюється до вигляду:

{\frac {1}{2}}S_{1}=-2\int \limits _{\sqrt {2a}}^{0}{\sqrt {(2a-u^{2})^{3}}}\,du=

=\left.-2\left({\frac {u}{8}}(10a-2u^{2}){\sqrt {2a-u^{2}}}+{\frac {3a^{2}}{2}}\arcsin {\frac {u}{\sqrt {2a}}}\right)\right|_{\sqrt {2a}}^{0}={\frac {3\pi a^{2}}{2}}.

Отже:

{\frac {1}{2}}S_{1}={\frac {3\pi a^{2}}{2}}.

S_{1}=3\pi a^{2}.

Об'єм тіла обертання

Об'єм ( $V_{1}$ ) тіла, утвореного при обертанні гілки $OL$ навколо осі абсцис, розраховується так:

V_{1}=\pi \int \limits _{0}^{2a}{\frac {x^{3}}{2a-x}}\,dx=

=\pi \int \limits _{0}^{2a}\left(-x^{2}-2ax-4a^{2}+{\frac {8a^{3}}{2a-x}}\right)\,dx=

=\left.-{\frac {44\pi a^{3}}{3}}-8\pi a^{3}(\ln(2a-x))\right|_{0}^{2a}.

Якщо $x\to 2a$ , то $\ln(2a-x)\to -\infty$ , тобто $V_{1}\to \infty$ .

Примітки

Акопян А.В. Геометрия в картинках.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Акопян А.В. Геометрия в картинках.