Чотирикутник Ламберта
В геометрії, чотирикутник Ламберта, названий на честь Йоганна Генріха Ламберта, який вперше досліджував властивості такої фігури в спробах довести п'яту аксіому геометрії Евкліда, є чотирикутником, в якому три з його кутів мають прямий кут. Історично склалося, що четвертий кут чотирикутника Ламберта приковув значний інтерес. В даний час відомо, що тип четвертого кута залежить від геометрії, в якій існує чотирикутник. У гіперболічної геометрії четвертий кут - гострий, в геометрії Евкліда він є прямим кутом, а в еліптичній геометрії це тупий кут.
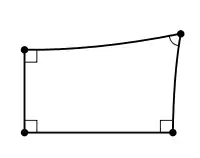
Властивості
Нехай — чотирикутник Ламберта на абсолютній площині з прямими кутами у вершинах , і . Тоді
- і ;
- .
Більше того, якщо одна з цих нерівностей перетворюється в рівність, то на цій абсолютній площині аксіома Евкліда вірна.
Історія
Чотирикутник Ламберта був вперше розглянутим Ібн аль-Хайсамом[1].
Розглядався Йоганном Ламбертом в 1766 при спробах довести аксіому паралельності Евкліда. З трьох можливих припущень про величину четвертого кута: або кут прямий, або кут тупий, або кут гострий; перша гіпотеза є твердженням, еквівалентним аксіомі паралельності Евкліда; друга призводить до протиріччя з іншими аксіомами і постулатами Евкліда. Щодо третьої гіпотези Ламберт зробив припущення, що вона виконується на деякій уявній сфері. Після чого зробив помилкове твердження, що такої сфери в реальному просторі бути не може і тому постулат вірний.
Аналогічну конструкцію розглядав Д. Саккері.