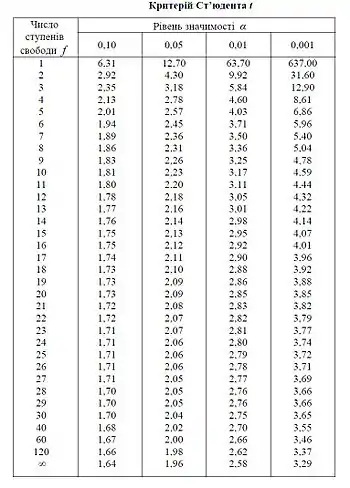
t-критерій Стьюдента

Цей критерій розробив був Вільям Ґоссет для оцінки якості пива в компанії Гіннес. У зв'язку із зобов'язаннями перед компанією не розголошувати комерційної таємниці (якою керівництво Гіннесу вважало таке використання статистичного апарату в своїй роботі), стаття Ґоссета вийшла в 1908 році в журналі «Біометрика» під псевдонімом «Student» (Студент).[2]

Для застосування названого критерію потрібно аби початкові дані мали нормальний розподіл. У разі застосування двовибіркового критерію для незалежних вибірок також потрібно дотримуватися умови рівности дисперсій. Існують, проте, альтернативи критерію Стьюдента для ситуації з нерівними дисперсіями.

У разі якщо розміри вибірок відрізняються мало, застосовують спрощену формулу наближених розрахунків:

${\displaystyle t={\frac {|M_{1}-M_{2}|}{\sqrt {{\frac {\sigma _{1}^{2}}{N_{1}}}+{\frac {\sigma _{2}^{2}}{N_{2}}}}}}}$

Коли розміри вибірок відрізняється значно, застосовується складніша і точніша формула:

${\displaystyle t={\frac {|M_{1}-M_{2}|}{\sqrt {{\frac {(N_{1}-1)\sigma _{1}^{2}+(N_{2}-1)\sigma _{2}^{2}}{N_{1}+N_{2}-2}}({\frac {1}{N_{1}}}+{\frac {1}{N_{2}}})}}}}$

Де ${\displaystyle M_{1},M_{2}}$ — середнє арифметичне, ${\displaystyle \sigma _{1},\sigma _{2}}$ — стандартне відхилення, а ${\displaystyle N_{1},N_{2}}$ — розміри вибірок.

Кількість ступенів свободи розраховують як

${\displaystyle \,df=N_{1}+N_{2}-2}$

Для обчислення емпіричного значення t-критерію в ситуації перевірки гіпотези про відмінності між двома залежними вибірками (наприклад, двома пробами одного і того ж тесту з часовим інтервалом) застосовують таку формулу:

${\displaystyle t={\frac {|M_{d}|}{\sigma _{d}/{\sqrt {N}}}}}$

де ${\displaystyle M_{d}}$ — середня різниця значень, а ${\displaystyle \sigma _{d}}$ — стандартне відхилення різниць.

Кількість ступенів свободи розраховують як

${\displaystyle \,df=N-1}$

Застосовується для перевірки гіпотези про відмінність середнього значення ${\displaystyle \,M_{x}}$ від деякого відомо значення ${\displaystyle \,A}$:

Кількість ступенів свободи розраховують як

${\displaystyle \,df=N-1}$

Аналогом двостороннього критерію для незалежних вибірок є U-критерій Манна-Уітні. Для ситуації із залежними вибірками аналогами є критерій знаків і T-критерій Вілкоксона.

• Статистичний критерій

• Ромакін В. В. Комп'ютерний аналіз даних: Навчальний посібник. — Миколаїв: Вид-во МДГУ ім. Петра Могили, 2006. — 144 с.