Аксіоми відокремлюваності

Діаграма Наса для аксіом відокремлюваності.

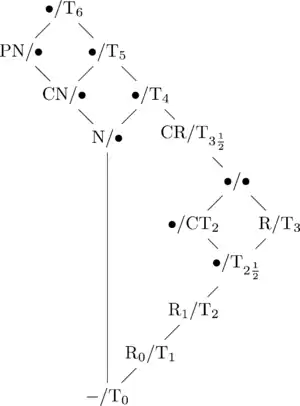
Для двох довільних різних точок ${\displaystyle \ x}$ та ${\displaystyle \ y}$ хоча б одна повинна мати окіл, що не містить другу точку.

Для двох довільних різних точок ${\displaystyle \ x}$ та ${\displaystyle \ y}$ повинен існувати окіл точки ${\displaystyle \ x}$, що не містить точку ${\displaystyle \ y}$ та окіл точки ${\displaystyle \ y}$, що не містить точку ${\displaystyle \ x}$.

Для двох довільних різних точок ${\displaystyle \ x}$ та ${\displaystyle \ y}$ повинні існувати околи ${\displaystyle U(x)}$ та ${\displaystyle V(y)}$, що не перетинаються.

Для двох довільних різних точок ${\displaystyle \ x}$ та ${\displaystyle \ y}$ повинні існувати замкнуті околи ${\displaystyle U(x)}$ та ${\displaystyle V(y)}$, що не перетинаються.

Для двох довільних різних точок ${\displaystyle \ x}$ та ${\displaystyle \ y}$ існує неперервна функція, рівна нулю на ${\displaystyle \ x}$ і одиниці на ${\displaystyle \ y}$.

Для довільної замкнутої множини і точки що не належить множині існують їх околи, що не перетинаються.

Для довільної замкнутої множини і точки що не належить множині існує неперервна функція, рівна нулю на множині і одиниці у точці.

Простори, що задовільняють аксіому T_3½ називаються повністю регулярними просторами чи тихонівськими просторами.

Для двох довільних замкнутих множин, що не перетинаються існують їх околи що не перетинаються.

• О. Я. Виро, О. А. Иванов, В. М. Харламов и Н. Ю. Нецветаев Задачный учебник по топологии
• Энгелькинг Р. Общая топология: Пер. с англ. — М.: Мир, 1986. — 752 с.

• Сепарабельний простір
• Принцип віддільності