Алгебраїчне доповнення

Нехай $\ A=(a_{ij})$ — квадратна матриця порядку $\ n$ , в якій вибрано:

Визначення

Алгебраїчне доповнення мінора $M_{j_{1},\ldots ,j_{k}}^{i_{1},\ldots ,i_{k}}$ визначається так:

A_{j_{1},\ldots ,j_{k}}^{i_{1},\ldots ,i_{k}}=(-1)^{p+q}\;{\overline {M}}_{j_{1},\ldots ,j_{k}}^{i_{1},\ldots ,i_{k}}

де

\ p=i_{1}+\ldots +i_{k},\quad q=j_{1}+\ldots +j_{k},

{\overline {M}}_{j_{1},\ldots ,j_{k}}^{i_{1},\ldots ,i_{k}}

Алгебраїчним доповненням елемента $\ a_{ij}$ називають мінор цього елемента, взятий зі знаком $\ (-1)^{i+j},$ тобто

\ A_{ij}=(-1)^{i+j}M_{ij}.

Мінор $\ M_{23}$ квадратної матриці $\ A$ — визначник матриці, отриманий шляхом викреслювання рядка 2 та стовпчика 3:

A={\begin{pmatrix}\,\,\,1&4&7\,\\\,\,\,3&0&5\,\\-1&9&\!11\,\\\end{pmatrix}},\qquad M_{23}={\begin{vmatrix}\,\,1&4&\Box \,\\\,\Box &\Box &\Box \,\\-1&9&\Box \,\\\end{vmatrix}}

\longrightarrow

{\begin{vmatrix}\,\,\,1&4\,\\-1&9\,\\\end{vmatrix}}=\left(9-\left(-4\right)\right)=13.

{\begin{vmatrix}2&3&-1\\1&4&2\\-3&1&4\\\end{vmatrix}}

Розв'язок:

Алгебраїчні доповнення до елементів а₂₁ та а₃₃ позначимо А₂₁ та А₃₃, відповідно.

Знаходження мінорів:

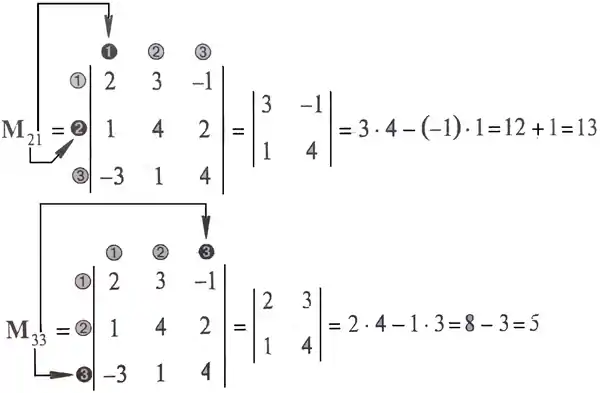
Підставимо ці значення мінорів у відповідні рівності (4), одержимо шукані алгебраїчні доповнення

А₂₁=(-1)²⁺¹ М₂₁= -13

А₃₃=(-1)³⁺³ М₃₃= 5

Гантмахер Ф. Р. Теория матриц. — 2 изд. — Москва : Наука, 1967. — 576 с. — ISBN 5-9221-0524-8.(рос.)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.