Теорія матриць
Теорія матриць — розділ математики, що вивчає властивості і застосування матриць.
Історія
Матриці мають довготривалу історію застосування при розв'язуванні систем лінійних рівнянь. Китайський текст «Математика в дев'яти книгах» (написаний ще до нашої ери) містить приклади використання матриць для розв'язання системи рівнянь, включаючи поняття визначника, ще задовго до введення визначників японським математиком Такакадзу Секі (1683) та німецьким математиком Лейбніцем (1693). Габріель Крамер представив своє правило в 1750 році.
Поняття «матриці», яке вже не було похідним від поняття «визначник» з'явилось тільки в 1858 році в праці англійського математика Артура Келі. Термін «матриця» першим став вживати Джеймс Джозеф Сильвестр, який розглядав матрицю, як об’єкт, що породжує сімейство мінорів (визначників менших матриць, утворених викреслюванням рядків та стовпців з початкової матриці).
Вивчення визначників відбувалось в різних галузях математики:
- Карл Фрідріх Гаус першим встановив зв’язок між квадратичними формами, лінійними відображеннями та матрицями.
- Коші розглядав визначники як многочлени та в 1829 довів, що власні значення симетричних матриць є дійсними числами.
Багато теорем доводили спочатку для матриць малих розмірів: теорема Гамільтона — Келі була доведена Келі тільки для матриць 2×2, а Гамільтоном для 4×4.
Поняття та характеристики
Основні поняття
Квадратні матриці
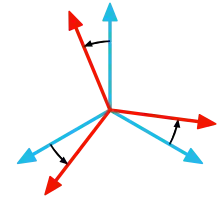
Квадратні матриці застосовують для опису лінійного перетворення векторного простору. Тому їх властивості доцільно вивчати знаючи теми: власний вектор та власне значення матриці із розділу лінійна алгебра.
Становлять інтерес такі квадратні матриці:
- вироджені, невироджені, обернена;
- переставні, подібні, конгруентні;
- нормальні, унітарні/ортогональні, самоспряжені/симетричні, косоермітові/кососиметричні;
- додатноозначені, проекційні;
- діагональні, одиничні.
Також для квадратних матриць існують такі важливі характеристики як визначник та слід.
Прямокутні матриці

(Квадратних матриць це також стосується).
Прямокутні матриці застосовуються для розв'язку систем лінійних рівнянь.
Тому потрібно вивчити поняття:
- трикутна матриця,
- псевдообернена матриця, формула Гревіля,
- сингулярний розклад матриці,
- QR розклад матриці,
- полярний розклад матриці.
Також для прямокутних матриць існує така важлива характеристика як ранг.
Блочні матриці
Застосування в аналітичній геометрії
Для аналітичної геометрії використовуються такі ортогональні матриці:
Застосування в теорії графів
Застосування в цифровій обробці сигналів (DSP)
Література
- Гантмахер Ф. Р. Теория матриц. — М. : Физматлит, 2010. — 560 с.
- Голуб Дж., ван Лоун Ч. Матричные вычисления. — М. : Мир, 1999. — 548 с.
- Ланкастер П. Теория матриц. — М. : Наука, 1982. — 272 с.
