Квадратна матриця
У математиці, квадратна матриця — це матриця з однаковою кількістю рядків і стовпців. -матриця — це квадратна матриця порядку :
- .
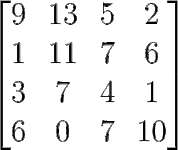
Числа називаються елементами матриці. Положення кожного елемента в матриці визначається номерами рядка і стовпчика, в яких знаходиться цей елемент. Наприклад, елемент знаходиться в -му рядку та -му стовпчику матриці . Це положення часто позначається індексами.
Будь-які дві квадратні матриці одного порядку можна додати та перемножити. Квадратні матриці часто використовують для зображення простих лінійних перетворень, таких як перетворення зсуву чи обертання. Наприклад, якщо — квадратна матриця, що представляє обертання ( матриця повороту), а — вектор-стовпець, що описує положення точки в просторі, добуток визначає інший вектор-стовпець, що описує положення цієї точки після цього обертання. Якщо — вектор-рядок, то те саме перетворення можна отримати, використовуючи , де — транспонована матриця .
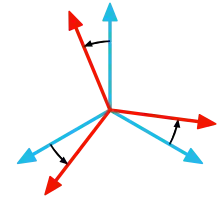
Головна діагональ
Елементи утворюють головну діагональ квадратної матриці. Вони лежать на уявній лінії, яка проходить від лівого верхнього кута до правого нижнього кута матриці. Наприклад, основана діагональ -матриці на рисунку містить елементи , , , .
Діагональ квадратної матриці, яка проходить від правого верхнього кута до нижнього лівого кута, називається побічною.
Спеціальні види
Назва Приклад з n = 3 Діагональна матриця Нижньо трикутна матриця Верхньо трикутна матриця
Діагональна або трикутна матриця
Якщо всі елементи за межами основної діагоналі дорівнюють нулю, називається діагональною матрицею. Якщо тільки всі елементи вище (або нижче) основної діагоналі дорівнюють нулю, називається нижньо (або верхньо) трикутною матрицею.
Одинична матриця
Одинична матриця розміру — це -матриця, у якій всі елементи на головній діагоналі рівні , а всі інші елементи дорівнюють , наприклад
Це квадратна матриця порядку , а також особливий вид діагональної матриці. Її називають одиничною матрицею, оскільки добуток з нею залишає матрицю незмінною:
- для будь-якої -матриці .
Симетрична або кососиметрична матриця
Квадратна матриця , яка дорівнює її транспонованій, тобто , називається симетричною матрицею. Якщо дорівнюватиме його транспонованій матриці з мінусом, тобто , то називається кососиметричною матрицею. У комплексних матрицях симетрію часто замінюють поняттям ермітових матриць, які задовольняють рівності , де — ермітово-спряжена матриця, тобто транспонована комплексно-спряжена матриця.
За спектральною теоремою, дійсні симетричні (або комплексні ермітові) матриці мають ортогональний (або ортонормований) базис, тобто кожен вектор виражається через лінійну комбінацію власних векторів. В обох випадках усі власні значення є дійсними.[1] Цю теорему можна узагальнити до нескінченновимірного випадку, пов'язаного з матрицями, які мають нескінченно багато рядків і стовпців.
Обернена матриця
Квадратну матрицю називають невиродженою (або несингулярною), якщо існує матриця така, що [2]
Якщо існує, то вона єдина і називається оберненою матрицею до матриці і позначається .
Нормальна матриця
Квадратну матрицю називають нормальною, якщо , тобто якщо вона комутує з своєю транспонованою матрицею.
Додатно та від'ємно визначені матриці
| Додатно визначена | Невизначена |
|---|---|
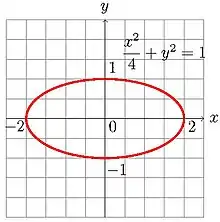 Точки для яких = 1 ( еліпс). |
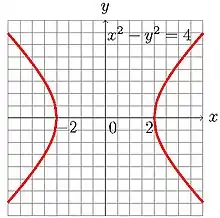 Точки для яких = 1 ( гіпербола). |
Симетричну -матриця називають додатно визначеною (відповідно від'ємно визначеною або невизначеною), якщо для всіх ненульових векторів відповідна квадратична форма
приймає лише додатні значення (відповідно лише від'ємні або як деякі від'ємні так і деякі додатні значення).[3] Якщо квадратична форма приймає лише невід'ємні значення (відповідно лише недодатні) значення, то симетрична матриця називається додатно напіввизначеною (відповідно від'ємно напіввизначена). Отже, матриця є невизначеною саме тоді, коли вона не є ні додатно напіввизначеною, ні від'ємно напіввизначеною.
Симетрична матриця є додатно визначеною тоді і лише тоді, коли всі її власні значення додатні[4]. У таблиці показано дві можливості для -матриць.
Якщо використати два різні вектори, то отримаємо білінійну форму пов'язану з матрицею : [5]
Ортогональна матриця
Ортогональна матриця — це квадратна матриця з дійсними елементами, стовпці та рядки якої є ортогональними одиничними векторами (тобто, ортонормованими векторами). Еквівалентно, матриця є ортогональною, якщо її транспонована матриця дорівнює її оберненій:
звідки випливає
де — одинична матриця.
Ортогональна матриця завжди має обернену (), унітарну () і нормальну ( матрицю. Визначник будь-якої ортогональної матриці дорівнює або , або . Спеціальна ортогональна матриця — ортогональна матриця з визначником . Як лінійне перетворення, кожна ортогональна матриця з визначником — це простий поворот, тоді як кожна ортогональна матриця з визначником є простим відзеркаленням, або суперпозицією віддзеркаленя і повороту.
Комплексний аналог ортогональної матриці — це унітарна матриця.
Операції
Слід
Слід квадратної матриці — це сума її елементів головної діагоналі. Хоча множення матриці не є комутативним, слід добутку двох матриць не залежить від порядку множників:
Це безпосередньо випливає з означення множення матриць:
Також слід матриці дорівнює сліду її транспонованої матриці, тобто
Визначник
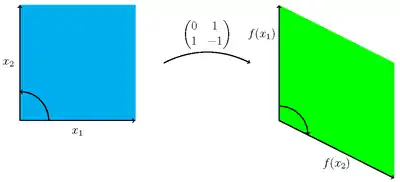
Визначник або квадратної матриці — це число, що визначає певні властивості матриці. Матриця є невиродженою тоді і лише тоді, коли її визначник ненульовий. Абсолютне значення визначника дорівнює площі (в ) або об'єму (в ) образу одиничного квадрату (або кубу), при цьому знак визначника відповідає орієнтації відповідного лінійного відображення, визначник додатній тоді і лише тоді, коли орієнтація зберігається. Визначник -матриць обчислюється за формулою
Визначник -матриць використовує 6 добутків (правило Сарруса). Більш довша формула Лейбница узагальнює ці дві формули для будь-якої розмірності.[6]
Визначник добутку квадратних матриць дорівнює добутку їх визначників:[7]
Додавання будь-якого рядка з коефіцієнтом до другого рядка, або будь-якого стовпця з коефіцієнтом до другого стовпця не змінює визначник. Перестановка місцями двох рядків або стовпців приводить до зміни знаку визначника.[8] За допомогою цих операцій будь-яка матриця може бути зведена на нижньо (або верхньо) трикутної матриці, а для таких матриць визначник дорівнює добутку елементів по головній діагоналі, що дає метод обчислювання визначника будь-якої матриці. Нарешті, теорема Лапласа виражає визначник у термінах мінорів, тобто визначників матриць меншої розмірності [9]. Ця теорема дає можливість рекурсивного обчислення визначників (починаючи з визначника -матриці, або навіть з визначника -матриці, який дорівнює 1), що можна розглядати як еквівалент формулі Лейбніца. Визначники можна використовувати для розв'язання лінійних систем за допомогою метода Крамера, де відношення визначників двох пов'язаних квадратних матриць дорівнює значенню кожної зі змінних системи.[10]
Лінійні перетворення векторного простору
Квадратні матриці застосовують для опису лінійного перетворення векторного простору.
Для запису лінійного перетворення матрицею в лінійному просторі потрібно вибрати базис.
Для дослідження властивостей лінійного перетворення використовують власні вектори та власні значення матриці.
Власні значення та власні вектори
Число і ненульовий вектор , що задовольняють рівності
називаються власним значенням та власним вектором матриці відповідно.[11][12] Число — власне значення -матриці тоді і лише тоді, коли матриця немає оберненої, що еквівалентно[13] умові
Многочлен (поліном) змінної , отриманий як визначник матриці , називається характерестичним многочленом матриці . Це нормований многочлен степеня . Тому рівняння має максимум різних коренів, тобто власних значень матриці.[14] Ці значення можуть бути комплексними, навіть якщо всі елементи матриці дійсні. Згідно теореми Гамільтона-Келі , , тобто при підстановці самої матриці в характеристичний многочлен, отримаємо нульову матрицю.
Див. також
Підвиди матриць:
Примітки
- Horn, Johnson 1985, Theorem 2.5.6
- Brown 1991, Definitions I.2.28 and Definition I.5.13
- Horn & Johnson 1985, Chapter 7
- Horn & Johnson 1985, Theorem 7.2.1
- Horn & Johnson 1985, Example 4.0.6, p. 169
- Brown 1991, Definition III.2.1
- Brown 1991, Theorem III.2.12
- Brown 1991, Corollary III.2.16
- Mirsky 1990, Theorem 1.4.1
- Brown 1991, Theorem III.3.18
- Eigen means ``own in German and in Dutch
- Brown 1991, Definition III.4.1
- Brown 1991,Definition III.4.9
- Brown 1991, Corollary III.4.10
Список літератури
- Brown, William C. (1991). Matrices and vector spaces. New York, NY: Marcel Dekker. ISBN 978-0-8247-8419-5.
- Horn, Roger A.; Johnson, Charles R. (1985). Matrix Analysis. Cambridge University Press. ISBN 978-0-521-38632-6.
- Mirsky, Leonid (1990). An Introduction to Linear Algebra. Courier Dover Publications. ISBN 978-0-486-66434-7.
- Гантмахер Ф. Р. Теория матриц. — 2 изд. — Москва : Наука, 1967. — 576 с. — ISBN 5-9221-0524-8.(рос.)
