Алгоритм Бентлі — Оттманна

Алгоритм Бентлі — Оттманна в обчислювальній геометрії використовує метод замітання прямою для пошуку всіх точок перетину прямолінійних відрізків на площині. Він узагальнює алгоритм Шеймоса-Нойї, який задану множину відрізків перевіряв на наявність будь-якого перетину. Для вхідних даних, які містять $n$ відрізків, що мають $k$ переринів, алгоритм Бентлі — Оттманна виконується за час ${\mathcal {O}}((n+k)\log n)$ . У випадку, коли $k={\mathcal {o}}\left({\frac {n^{2}}{\log n}}\right)$ , його можна розглядати як удосконалення алгоритму повного перебору, який виконується за час $\Theta (n^{2})$ .

Перетин відрізків

O\left(\left(n+k\right)\log n\right)

Алгоритм був розроблений Джоном Бентлі та Томасом Оттманном у 1979 році. Більш детально він описаний у книгах Preparata та Shamos, (1985), O'Rourke, (1998), та de Berg та ін., (2000). Хоча й відомі асимптотично більш швідкі алгоритми, алгоритм Бентлі — Оттманна залишається затребуваним завдяки простоті та використанню низького об'єму пам'яті^{[джерело?]}.

Загальний опис

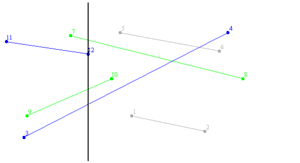
В алгоритмі застосовується метод замітаючої прямої (замітаючої прямої[1], що рухається прямо, скануючи лінії[2]; англ. sweeping line). У методі використовується вертикальна вимітаюча пряма, що рухається зліва направо, при цьому відрізки, які вона перетинає при даній координаті $x$ , можна впорядкувати за координатою $y$ , тим самим їх можна порівнювати між собою (котрий вище, котрий нижче). Це порівняння можна здійснити, наприклад, використовуючи рівняння прямої, що проходить через дві точки (відрізки задано двома своїми кінцевими точками): $\left(x-x_{1}\right)/\left(x_{2}-x_{1}\right)=\left(y-y_{1}\right)/\left(y_{2}-y_{1}\right)$ , де $x_{1}$ , $y_{1}$ і $x_{2}$ , $y_{2}$ — координати, відповідно, першої та другої точок відрізка. Вимітаюча пряма переміщається по так званим точкам подіям (лівим і правим кінцям відрізків, а також точкам перетину відрізків). Після точки перетину відрізки варто міняти місцями, оскільки, наприклад, самий верхній із відрізків, які перетинаються після точки перетину стає самим нижнім. Наведений нижче алгоритм не розрахований на випадок, коли два відрізки перетинаються більше, ніж в одній точці.

NB Вимітаючу пряму можна також представити як горизонтальну, що рухається згори до низу за координатою $y$ , і порівнювати відрізки, що її перетинають за координатою $x$ .

Обробка вертикальних відрізків

Виникає проблема з вертикальним відрізком у тому розумінні як його порівнювати на вище/нижче з відрізками, що перетинають. Для цього можна, наприклад, вважати, що якщо точка перетину вертикального з не вертикальним відрізків знаходиться нижче поточної координати $y$ точки події, то вертикальний відрізок знаходиться вище, якщо точка перетину вище поточної координати $y$ точки події, то вертикальний відрізок вважається нижче відрізка, що перетинає його. Якщо поточна координата $y$ дорівнює координаті $y$ точки події, то при видаленні відрізка вважати, що вертикальний відрізок нижче, а при вставленні вважати, що він вище.

Квадрат пам'яті

У гіршому випадку, коли, наприклад, усі відрізки, перетинаючись між собою, утворюють прямокутну сітку, буде $O\left(n^{2}\right)$ точок перетину, які потрібно буде зберігати. Щоб уникнути використання квадрата пам'яті в алгоритмі, можна видаляти точку перетину відрізків, котрі тимчасово перестають бути сусідніми при даному положенні вимітаючою прямою. Ці точки все рівно будуть знову знайдені при подальших кроках алгоритму, коли дані відрізки знову стануть сусідніми (Печ, Шерір 1991).

Алгоритм

У наведеному нижче псевдокоді використовуються:

Q — динамічні структура даних без повторень з логарифмічним часом пошуку, вставки, видалення точок подій і пошуку мінімального елемента (наприклад, червоно-чорне дерево, 2-3-дерево).
T — динамічні структура даних без повторень з логарифмічним часом пошуку, вставки, видалення відрізків. У ній зберігаються всі відрізки, що перетинають вимітаючу пряму (наприклад, червоно-чорне дерево, 2-3-дерево).
q — точка події.
newq — щойно знайдена точка перетину відрізків, точка події.
L(q) — безліч відрізків, лівий кінець яких — q (для вертикальних відрізків лівим вважається нижній кінець).
R(q) — безліч відрізків, правим кінцем яких є q.
I(q) — безліч відрізків, що перетинаються в q.

segmentsIntersections(points[])
    1) Ініціалізуються Q і T. До Q заносяться всі кінці відрізків, впорядковані за координатою x, при цьому, якщо дві точки збігаються,
       то ліва кінцева точка відрізка поміщається перед правою. Якщо збігаються лише x, то точка з меншим y є меншою.
       T ← ∅
    2) while Q != ∅
           q ← min(Q);
           processPoint(q);

processPoint(q)
    1) Знайти в Q всі відрізки, які містять q; // вони в Q будуть сусідніми, оскільки точки події, що містяться в цих відрізках, мають однакові координати;
    2) if (|L(q)| + |R(q)| + |I(q)| > 1) АБО (|I(q)| > 0)
           then Видати у відповідь точку q;
    3) if (|I(q)| = 0) І (|L(q)|+|R(q)| > 0) // у точці, яка розглядається, всі відрізки лише починаються або закінчуються;
           then I(q) ← I(q) ∪ L(q) ∪ R(q); // додати в I(q) L(q) і R(q)
    4) Видалити з T R(q) і I(q);
    5) Вставити в T I(q) і L(q);
    // із T були видалені всі відрізки з безліччю I(q), тепер же вставляються назад у зміненому порядку після точки перетину;
    6) if (L(q)∪I(q) = ∅) АБО (|I(q)| = |R(q)| - 1)
           then Знайти в T верхнього та нижнього сусідів q su і sl;
                newq = findIntersect(su, sl);
                if newq != NULL
                    then add(Q, newq);
    7) else
           Нехай s′ — самий верхній відрізок із L(q)∪I(q);
           Нехай su — верхній сусід s′ в T;
           Нехай s′′ — самий нижній відрізок із L(q)∪ I(q);
           Нехай sl — нижній сусід s′′ в T;
           newq = findIntersect(su, s′);
           if newq != NULL
               then add(Q, newq);
           newq = findIntersect(sl, s′′);
           if newq != NULL
               then add(Q, newq);
           // далі прибираємо квадрат пам'яті;
           newq = findIntersect(sl, su);
           if newq != NULL
               then delete(Q, newq);
           newq = findIntersect(s′′, su);
           if newq != NULL
               then delete(Q, newq);
           newq = findIntersect(sl, s′);
           if newq != NULL
               then delete(Q, newq);

findIntersect(sl, su)
    if sl і su перетинаються праворуч від замітаючої прямої (або на замітаючій прямій вище поточної точки подій)
        then return newq;
    else return NULL;

Аналіз

Нехай $n$ — число відрізків, $m\left(q\right)$ — число відрізків, що перетинають точку $q$ . Тоді час на ініціалізацію Q дорівнює $O\left(n\log n\right)$ , на ініціалізацію T — $O\left(1\right)$ . На пошук усіх відрізків, що проходять через точку $q$ і оновлення Q, потрібно $O\left(m\left(q\right)\log n\right)$ часу. На оновлення T також $O\left(m\left(q\right)\log n\right)$ часу. Сумарно: $O\left(n\log n+\sum m\left(q\right)\log n\right)=O\left(n\log n+\log n\sum m\left(q\right)\right)=O\left(\left(n+k\right)\log n\right)$ , де $k$ — число точок перетину $\left(\sum m\left(q\right)=O\left(n+k\right)\right)$ . $k=O\left(n^{2}\right)$ .

Пам'ять $O\left(n\right)$ , завдяки тому, що віддаляються точки перетину відрізків, котрі перестали бути сусідніми, інакше було б $O\left(n+k\right)$ , де $k=O\left(n^{2}\right)$ .

Примітки

Прапарата Ф., Шеймос М. Обчислювальна геометрія: Вступ = Computational Geometry An introduction. — М. : Мир, 1989. — 478 с.
Ласло М. Обчислювальна геометрія та комп'ютерна графіка на C++. — М. : БИНОМ, 1997. — 304 с.

Література

Берг М., Чеонг О., Кревельд М., Овермарс М. Вычислительная геометрия. Алгоритмы и приложения = Computational Geometry: Algorithms and Applications. — М. : ДМК-Пресс, 2016. — 438 с. — ISBN 978-5-97060-406-9.
Mark de Berg, Marc van Kreveld, Mark Overmars, Otfried Schwarzkopf. Computational Geometry: Algorithms and Applications. — Springer, 2000. — 368 с.
Прапарата Ф., Шеймос М. Вычислительная геометрия: Введение = Computational Geometry An introduction. — М. : Мир, 1989. — 478 с.
Ласло М. Вычислительная геометрия и компьютерная графика на C++. — М. : БИНОМ, 1997. — 304 с.
Т. Кормен, Ч. Лейзерсон, Р. Рівест, К. Штайн. Алгоритми. Побудова й аналіз = Introduction to Algorithms. — 2-e вид. — “Вільямс”, 2005. — 1296 с.

Balaban, I. J. (1995). An optimal algorithm for finding segments intersections. Proc. 11th ACM Symp. Computational Geometry. с. 211–219. doi:10.1145/220279.220302..
Bartuschka, U.; Mehlhorn, K.; Näher, S. (1997). A robust and efficient implementation of a sweep line algorithm for the straight line segment intersection problem. У Italiano, G. F.; Orlando, S. Proc. Worksh. Algorithm Engineering. Архів оригіналу за 6 червня 2017. Процитовано 23 листопада 2018..
Bentley, J. L.; Ottmann, T. A. (1979). Algorithms for reporting and counting geometric intersections. IEEE Transactions on Computers C–28 (9): 643–647. doi:10.1109/TC.1979.1675432..
de Berg, Mark; van Kreveld, Marc; Overmars, Mark; Schwarzkopf, Otfried (2000). Chapter 2: Line segment intersection. Computational Geometry (вид. 2nd). Springer-Verlag. с. 19–44. ISBN 978-3-540-65620-3..
Boissonat, J.-D.; Preparata, F. P. (2000). Robust plane sweep for intersecting segments. SIAM Journal on Computing 29 (5): 1401–1421. doi:10.1137/S0097539797329373..
Brown, K. Q. (1981). Comments on "Algorithms for Reporting and Counting Geometric Intersections". IEEE Transactions on Computers C–30 (2): 147. doi:10.1109/tc.1981.6312179..
Chazelle, Bernard; Edelsbrunner, Herbert (1992). An optimal algorithm for intersecting line segments in the plane. Journal of the ACM 39 (1): 1–54. doi:10.1145/147508.147511..
Chen, E. Y.; Chan, T. M. (2003). A space-efficient algorithm for segment intersection. Proc. 15th Canadian Conference on Computational Geometry..
Clarkson, K. L. (1988). Applications of random sampling in computational geometry, II. Proc. 4th ACM Symp. Computational Geometry. с. 1–11. doi:10.1145/73393.73394..
Clarkson, K. L.; Cole, R.; Tarjan, R. E. (1992). Randomized parallel algorithms for trapezoidal diagrams. International Journal of Computational Geometry and Applications 2 (2): 117–133. doi:10.1142/S0218195992000081.. Corrigendum, 2 (3): 341–343.
Eppstein, D.; Goodrich, M.; Strash, D. (2009). Linear-time algorithms for geometric graphs with sublinearly many crossings. Proc. 20th ACM-SIAM Symp. Discrete Algorithms (SODA 2009). с. 150–159. Bibcode:2008arXiv0812.0893E. arXiv:0812.0893..
Mulmuley, K. (1988). A fast planar partition algorithm, I. Proc. 29th IEEE Symp. Foundations of Computer Science (FOCS 1988). с. 580–589. doi:10.1109/SFCS.1988.21974..
O'Rourke, J. (1998). Section 7.7: Intersection of segments. Computational Geometry in C (вид. 2nd). Cambridge University Press. с. 263–265. ISBN 978-0-521-64976-6..
Preparata, F. P.; Shamos, M. I. (1985). Section 7.2.3: Intersection of line segments. Computational Geometry: An Introduction. Springer-Verlag. с. 278–287..
Pach, J.; Sharir, M. (1991). On vertical visibility in arrangements of segments and the queue size in the Bentley–Ottmann line sweeping algorithm. SIAM Journal on Computing 20 (3): 460–470. MR 1094525. doi:10.1137/0220029..
Shamos, M. I.; Hoey, Dan (1976). Geometric intersection problems. 17th IEEE Conf. Foundations of Computer Science (FOCS 1976). с. 208–215. doi:10.1109/SFCS.1976.16..

Посилання

Візуалізатор — окремий випадок (алгоритм Шеймоса — Гоя, 1976 (Визначення наявності відрізків, що перетинаються)).
Smid, Michiel (2003). Computing intersections in a set of line segments: the Bentley–Ottmann algorithm.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Прапарата Ф., Шеймос М. Обчислювальна геометрія: Вступ = Computational Geometry An introduction. — М. : Мир, 1989. — 478 с.

[2] Ласло М. Обчислювальна геометрія та комп'ютерна графіка на C++. — М. : БИНОМ, 1997. — 304 с.