Алгоритм обміну XOR
У комп'ютерному програмуванні, XOR обмін (англ. XOR swap) — алгоритм, який використовує бітову операцію XOR для обміну значень різних змінних однакового типу даних без використання додаткової тимчасової змінної. Під словом «різні» мається на увазі, що значення змінних зберігається в різних адресах пам'яті; фактичні значення змінних не обов'язково повинні бути різними.
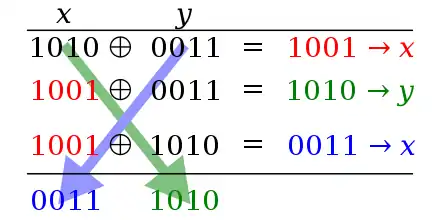
Алгоритм
Традиційний обмін значеннями потребує використання тимчасової змінної для збереження. При використанні алгоритму XOR обміну, не потрібно мати тимчасового збереження. Алгоритм виконується наступним чином:[1][2]
X := X XOR Y
Y := Y XOR X
X := X XOR Y
Алгоритм зазвичай відповідає трьом інструкціям машинного коду. Оскільки XOR є комутативною операцією, X XOR Y можна замінити на Y XOR X у будь-якому з цих рядків. При написанні коду на мові асемблер, ця комутативність часто використовується в другому рядку:
| Псевдокод | IBM System/370 асемблер | x86 асемблер |
|---|---|---|
X := X XOR Y | XR R1,R2 | xor eax, ebx |
Y := Y XOR X | XR R2,R1 | xor ebx, eax |
X := X XOR Y | XR R1,R2 | xor eax, ebx |
У приведеному вище коді асемблеру для System/370, R1 і R2 є різними регістрами, і кожна операція XR записує свій результат у регістрі, що вказаний першим аргументом. При використанні асемблеру x86, значення X і Y знаходяться в регістрах eax і ebx (відповідно), а xor записує результат операції в перший регістр.
Однак, алгоритм не буде виконуватись, якщо x і y використовують одне сховище пам'яті, оскільки значення, що знаходиться за однією адресою будуть мати нульові значення після виконання першої інструкції XOR, і потім залишаться нулями; і це не буде заміною.
Доведення справедливості
Бітова операція XOR над послідовностями біт довжини має наступні властивості (де позначає XOR):[lower-alpha 1]
- L1. Комутативність:
- L2. Асоціативність:
- L3. Існування нейтральності: існує бітова послідовність, 0, (довжиною N), для якої виконується для будь-якого
- L4. Кожен елемент є своїм власним оберненим: для кожного , .
Припустимо, що ми маємо два різні регістри R1 і R2 як показано нижче в таблиці, які мають початкові значення A і B відповідно. Виконаємо приведені нижче операції по черзі, і виконаємо спрощення за допомогою наведених вище властивостей.
| Крок | Операція | Регістр 1 | Регістр 2 | Перетворення |
|---|---|---|---|---|
| 0 | Початкове значення | — | ||
| 1 | R1 := R1 XOR R2 | — | ||
| 2 | R2 := R1 XOR R2 | L2 L4 L3 | ||
| 3 | R1 := R1 XOR R2 | L1 L2 L4 L1 L3 |
Причини використання на практиці
Здебільшого, звичайний алгоритм обміну з використанням тимчасового регістру більш ефективний. Конкретні ситуації, в яких практично корисно застосувати XOR обмін є наступні:
- у процесорах де набір інструкцій дозволяє виконувати XOR обмін закодований за допомогою меншої кількості байт;
- у випадках з постійною нестачею вільних регістрів, це може дозволити уникнути застосування пам'яті замість регістрів;
- у мікроконтролерах де доступна пам'ять RAM дуже обмежена.
Оскільки ці ситуації не є частим, більшість оптимізувальних компіляторів ніколи не генерують коду з XOR обміном.
Приклад реалізації
За допомогою препроцесора мови C, цю функцію можна реалізувати наступним чином:
#define swapXOR(x,y) do { *x ^= *y; *y ^= *x; *x ^= *y; } while(0)
int main (int argc, char** argv) {
int x = 5;
int y = 7;
printf("%i, %i\n", x,y); // до заміни 5, 7
swapXOR(&x,&y);
printf("%i, %i\n", x,y); // після 7, 5
}
Див. також
Примітки
- The Magic of XOR. Cs.umd.edu. Процитовано 2 квітня 2014.
- Swapping Values with XOR. graphics.stanford.edu. Процитовано 2 травня 2014.
- Перші три властивості, разом із існуванням інверсії кожного з елементів, є визначенням абелевої групи. Остання властивість, є структурною особливістю XOR і не обов'язково поширюється на інші Абелеві групи.