Алмаз (теорія графів)

Алмаз — це планарний неорієнтований граф із 4 вершинами та 5 ребрами[1][2]. Граф являє собою повний граф без одного ребра.

Алмаз
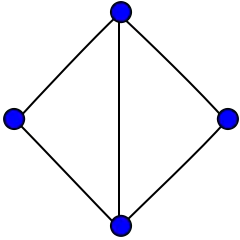Вершин 4
Ребер 5
Радіус 1
Діаметр 2
Обхват 3
Автоморфізм 4 (Z/2Z×Z/2Z)
Дробово-хроматичне число 3
Дробово-хроматичний індекс 3
Властивості Граф одиничних відстаней
Планарний
Гамільтонів

Радіус алмаза дорівнює 1, діаметр дорівнює 2, обхват дорівнює 3, хроматичний індекс і хроматичне число дорівнюють 3. Граф також вершинно 2-зв'язаний і реберно 2-зв'язаний, має граціозну розмітку[3] і є гамільтоновим.

Графи без алмазів і заборонені мінори

Граф є вільним від алмазів, якщо він не містить алмаза в якості породженого підграфа. Графи без трикутників є вільними від алмазів, оскільки будь-який алмаз містить трикутник.

Сімейство графів, в якому кожна зв'язна компонента є кактусом, замкнуто донизу відносно операції утворення мінору графа. Це сімейство графів може бути описано єдиним забороненим мінором — алмазом[4].

Якщо метелик й алмаз є забороненими мінорами, отримане сімейство графів є сімейством псевдолісів.

Алгебраїчні властивості

Група автоморфізмів алмаза є групою порядку 4, ізоморфною четверній групі Клейна, прямому добутку циклічної групи Z/2Z на себе.

Характеристичний многочлен алмаза дорівнює . Алмаз є єдиним графом із характеристичним многочленом, що визначає граф за його спектром.

Примітки
  1. Weisstein, Eric W. Diamond Graph(англ.) на сайті Wolfram MathWorld.
  2. ISGCI: Information System on Graph Classes and their Inclusions "List of Small Graphs".
  3. Sin-Min Lee, Y.C. Pan and Ming-Chen Tsai. "On Vertex-graceful (p,p+l)-Graphs". Архівована копія. Архів оригіналу за 7 серпня 2008. Процитовано 16 вересня 2009.
  4. El-Mallah, Colbourn, 1988, с. 354–362.

Література
  • Ehab El-Mallah, Charles J. Colbourn. The complexity of some edge deletion problems // IEEE Transactions on Circuits and Systems. — 1988. — Т. 35, вип. 3. — С. 354–362. — DOI:10.1109/31.1748.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.