Обхват (теорія графів)

Кубічні графи (всі вершини мають степінь три) з якомога меншим обхватом ${\displaystyle g}$ відомі як ${\displaystyle g}$-клітка (або як (3,${\displaystyle g}$)-клітка). Граф Петерсена — це єдина 5-клітка (найменший кубічний граф з обхватом 5), граф Хівуда — це єдина 6-клітка, Граф Маꥳ — це єдина 7-клітка, а граф Татта — Коксетера — це єдина 8-клітка[3]. Може існувати кілька кліток для даного обхвату. Наприклад, існує три неізоморфних 10-клітки, кожна з 70 вершинами — 10-клітка Балабана, граф Харріса і граф Харріса—Вона.

• 
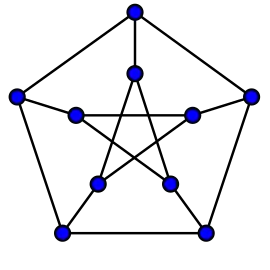  Граф Петерсена має обхват 5
• 
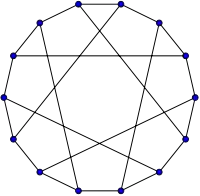  Граф Хівуда має обхват 6
• 
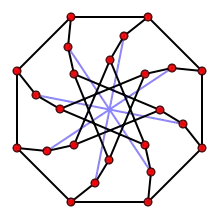  Граф Маꥳ має обхват 7
• 
  Граф Татта — Коксетера (8-клітка Татта) має обхват 8

Для будь-якого додатного цілого ${\displaystyle k}$ існує граф ${\displaystyle G}$ з обхватом ${\displaystyle g(G)\geqslant k}$ і хроматичним числом ${\displaystyle \chi (G)\geqslant k}$. Наприклад, граф Грьотча є графом без трикутників і має хроматичне число 4, а багаторазове повторення конструкції Мицельскіана, що використовується для створення графу Грьотча, утворює графи без трикутників з як завгодно великим хроматичним числом. Пол Ердеш довів цю теорему, використовуючи імовірнісний метод.[4]

План доведення. Назвемо цикли довжиною не більше ${\displaystyle k}$ короткими, а множини з ${\displaystyle |G|/k}$ і більше вершин — великими. Для доведення теореми достатньо знайти граф ${\displaystyle G}$ без коротких циклів і великих незалежних множин вершин. Тоді множина кольорів в розфарбовуванні не будуть більшими, і, як наслідок, для розфарбування потрібно ${\displaystyle k}$ кольорів.

Щоб знайти такий граф, будемо фіксувати ймовірність вибору ${\displaystyle p}$, що дорівнює ${\displaystyle n^{\varepsilon -1}}$. При маленьких ${\displaystyle \varepsilon }$ в ${\displaystyle G}$ виникає лише мале число коротких циклів. Якщо тепер видалити по вершині з кожного такого циклу, отриманий граф ${\displaystyle H}$ не матиме коротких циклів, а його число незалежності буде не менше, ніж у графу ${\displaystyle G}$[1].

Непарний обхват і парний обхват графу — це коли довжина найменшого непарного циклу і найменшого парного циклу відповідно.

Окружність графу — це довжина найбільшого по довжині циклу, а не найменшого.

Спроби оцінити довжину найменшого нетривіального циклу можна розглядати як узагальнення 1-систоли або більшої систоли в систолічній геометрії.