Відстань (теорія графів)

Метричний простір визначений на множині вершин за допомогою відстаней на графі називається метрикою графу. Множина вершин (не орієнтованого графу) і ця функція відстаней утворюють метричний простір тоді, і тільки тоді, коли граф є зв'язним.

Ексцентриситет ${\displaystyle \epsilon (v)}$ вершини ${\displaystyle v}$ — це найбільша геодезична відстань між ${\displaystyle v}$ і будь-якою іншою вершиною.

Радіус ${\displaystyle r}$ графу — це мінімальний ексцентриситет будь-якої з вершин графу або, символьно, ${\displaystyle r=\min _{v\in V}\epsilon (v)}$.

Діаметр ${\displaystyle d}$ графу — це максимальний ексцентриситет будь-якої з вершин графу. Тобто, ${\displaystyle d}$ — це найдовша відстань між будь-якою двійкою вершин, ${\displaystyle d=\max _{v\in V}\epsilon (v)}$. Щоб знайти діаметр графу спочатку знайдіть найкоротші шляхи між кожною двійкою вершин графу. Найбільша довжина серед цих шляхів і є діаметром графу.

Центральна вершина графу — це вершина, ексцентриситет якої дорівнює радіусу графу, тобто ${\displaystyle \epsilon (v)=r}$.

Зеленим позначені псевдопериферійні вершини. Діаметр графу 4. ${\displaystyle \epsilon (9)=\epsilon (4)<4,\epsilon (8)=\epsilon (4)<4}$

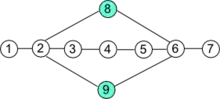
Периферійна вершина графу діаметру ${\displaystyle d}$ — це така вершина ${\displaystyle v}$, що ${\displaystyle \epsilon (v)=d}$.

Псевдопериферійна вершина ${\displaystyle v}$ має властивість, що для будь-якої вершини ${\displaystyle u}$, якщо ${\displaystyle v}$ є якнайдалі від ${\displaystyle u}$, тоді й ${\displaystyle u}$ є якнайдалі ${\displaystyle v}$. Формально, вершина u псевдопериферійна, якщо для кожної вершини v для якої ${\displaystyle d(u,v)=\epsilon (u)}$ виконується ${\displaystyle \epsilon (u)=\epsilon (v)}$.

Розбиття вершин графу на підмножини згідно з їх відстанями від певної вершини називається рівневою структурою графу.

Граф, у якому для кожної двійки вершин існує унікальний найкоротший шлях, що сполучає їх, називається геодезичним графом. Наприклад, дерево — це геодезичний граф.[4]

Часто алгоритмам для побудови розріджених матриць з найменшим розкидом елементів від головної діагоналі необхідна вершина з високим ексцентриситетом, наприклад дивись алгоритм Катхілл-Маккі. Периферійна вершина підійшла б найкраще, але таку вершину часто важко знайти. Зазвичай можна використати псевдопериферійну вершину. Таку вершину легко знайти за допомогою такого алгоритму:

1. Обрати вершину ${\displaystyle u}$.
2. Серед усіх вершин, що є якнайдалі від ${\displaystyle u}$, нехай ${\displaystyle v}$ буде такою, що має мінімальний степінь.
3. Якщо ${\displaystyle \epsilon (v)>\epsilon (u)}$ тоді встановити ${\displaystyle u=v}$ і повторити крок 2, інакше ${\displaystyle v}$ — це псевдопериферійна вершина.

• Матриця відстаней