Випадкова подія
Випадкова подія — подія, яка при заданих умовах може як відбутись, так і не відбутись, при чому існує визначена ймовірність p (0 ≤ p ≤ 1) того, що вона відбудеться при заданих умовах. Випадкова подія є підмножиною простору елементарних подій. Кожна випадкова подія є наслідком великої кількості випадкових причин які врахувати немає можливості оскільки число їх дуже велике і закони їхні невідомі. Випадковими подіями називаються підмножини простору елементарних подій, що є відповідними прообразами певних висловлювань про результат стохастичного експерименту. Подія — це результат випробування. Всі події які ми спостерігаємо діляться на: достовірні, неможливі та випадкові. Події позначаються великими латинськими буквами . або однією латинською буквою з індексом: . Зміст події подають у фігурних дужках. Наприклад: настав ранок[1]. Сказати наперед про випадкову подію, що відбудеться чи не відбудеться, не можна. Прийнято вважати, що неможлива і вірогідна події — окремі випадки випадкової події. Наприклад, підкидають гральний кубик (однорідний кубик правильної форми). Маємо шість подій попарно несумісних, однаково можливі. У такому разі вважають, що для здійснення кожної події існує один шанс із шести. Наприклад, імовірність того, що на підкинутому гральному кубику випаде 5 очок, дорівнює [2].
| Частина серії статей з статистики |
| Теорія ймовірностей |
|---|
 |
|
|
|
Те, що випадкова подія має деяку ймовірність проявляється в поведінці її частоти: якщо вказані умови повторити раз, а подія відбудеться при цьому раз, то частота реалізації події при великих стає близькою до .
Подія може вважатися випадковою лише коли вона може повторитись довільну кількість разів. Якщо в n випробуваннях подія А відбувається m разів, то дріб визначає відносну частоту появи події А. Число, біля якого коливається відносна частота події, виражає ймовірність цієї події; її позначають буквою Р (від англійського слова probability — імовірність).
Ймовірність достовірної події дорівнює 1. Ймовірність неможливої події дорівнює 0. Ймовірність випадкової події більше 0 і менше 1: 0 P(A) 1.[3]
Формат запису
Події є підмножинами деякого простору елементарних подій Ω, тому вони часто записуються в формі предикатів, що включають випадкові величини. Наприклад, якщо X це дійсна випадкова величина визначена на просторі Ω, подія
може бути записана більш просто, так:
Цей запис звичніший для формул з ймовірністю, наприклад:
Алгебра подій
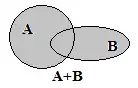
Нехай є дві події А і В. Якщо з того, що настала подія А слідує, що настане подія В, то подія В є частинним випадком події А, тобто B A.
Якщо B A і AB , тоді ці події називають рівними.
Операції над подіями:
- Сумою двох подій А і В називається подія А+В, яка полягає в появі хоча б однієї з них.
- Добутком двох подій А і В називається подія АВ, яка полягає в одночасній появі цих подій.
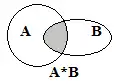 Добуток двох подій А і В
Добуток двох подій А і В - Різницею двох подій А і В називається подія А-В (А/В), яка полягає в появі події А і не появі події В.
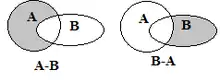 Різниця двох подій А і В
Різниця двох подій А і В - Протилежною до події А називається подія , яка полягає в ненастанні події А.
Події в ймовірнісних просторах
Визначення будь-якої підмножини вибіркового простору як події, працює добре, коли є скінченне число результатів, і створює проблеми коли вибірковий просторі нескінченний. Для багатьох стандартних розподілів ймовірності, таких як нормальний розподіл, вибірковий простір — це множина дійсних чисел або вся множина дійсних чисел. Спроби визначити ймовірності всіх підмножин множини дійсних чисел, стикаються з труднощами при розгляді тих наборів, що «погано себе поводять», наприклад, з невимірними. Отже, треба розглядати обмежену сім'ю підмножин.
Приклади
Приклади випадкової події:
- поява „герба” при підкиданні монети,
- виграш по даному лотерейному білету,
- збіг дати народження у двох навмання вибраних людей з певного міста,
- завтра буде хороша погода.
Задача 1. Знайти ймовірність того, що вибране випадковим чином двозначне число ділиться на: а) 3; б) 5.
Розв’язання. Випробування полягає в тому, що вибирається випадковим чином двозначне число. Наслідком такого випробування є одне з чисел від 10 до 99. Оскільки таких чисел 90, то n = 90.
а) Нехай подія А = {вибране двозначне число ділиться на 3}. Оскільки кожне третє з 90 двозначних чисел ділиться на 3, то сприятливими для події А є 30 наслідків, тобто m = 30. Тоді за формулою імовірність події .
б) Нехай подія В = {вибране двозначне число ділиться на 5}. Загальна кількість наслідків випробування, як і в попередньому випадку, n = 90. Визначимо кількість чисел, які діляться на 5. Очевидно, що таких чисел буде m = 18 (кожне п’яте число ділиться на 5). Отже, .
Задача 2. Монету підкидають три рази. Знайти ймовірності того що: а) A — герб випаде 1 раз. A — герб випаде 1 раз; г, г,г; г, г,ц; г, ц,г; ц, г,г; г, ц,ц; ц, г,ц; ц, ц,г; ц, ц,ц, n=8, m=3, P(A)=.
б) B — ні разу не випаде цифра. n=8, m=1, P(B)=.
в) C — герб випаде більше раз ніж цифра. C — герб випаде 2 або 3 рази. P(C)=.
Примітки
- Алгебра (Бевз) 9 клас 2017. Шкільні підручники онлайн (укр.). Процитовано 2 січня 2020.
- Алгебра 11 класс Бевз. Электронные учебники для школы. Скачать украинские учебники pdf. (рос.). Процитовано 2 січня 2020.
- Алгебра 10-11 клас Шкіль Слєпкань Дубинчук 2001. pick.net.ua. Процитовано 2 січня 2020.
Література
- Енциклопедія кібернетики, т. 2, ст. 377.
- Єжов С.М. (2001). Теорія ймовірностей, математична статистика і випадкові процеси: Навчальний посібник. (укр). К.: ВПЦ "Київський університет". Архів оригіналу за 24 лютого 2007. Процитовано 21 червня 2010.