Випадкове блукання

Випадкове блукання — математичний формалізм, що описує траєкторію, яка утворюється при здійсненні послідовних випадкових кроків. Багато різних типів випадкових блукань представляють інтерес. Найчастіше розглядаються випадкові блукання, які є ланцюгами Маркова, але інші, складніші види блукань також представляють інтерес. Деякі випадкові блукання здійснюються на графах, інші — на прямій, на площині або у більш високих розмірностях, тоді як деякі блукання здійснюються на групах. Випадкові блукання також розрізняються у відношенні до часового параметру. Найчастіше блукання відбувається у дискретному часі та індексується натуральними числами $X_{0},X_{1},X_{2},\dots$ . Однак деякі блукання здійснюють кроки у випадкові моменти часу, і в такому випадку координата $X_{t}$ визначена на неперервному промені $t\geq 0$ .

Одновимірне дискретне випадкове блукання

Графіки

X_{i}(i)

восьми одновимірних випадкових блукань.

Приклад двовимірного випадкового блукання. 229 кроків, довжина кроку від −0.5 до 0.5, рівноймовірні напрями

x

або

y

.

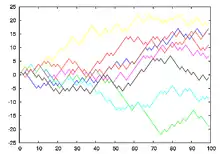
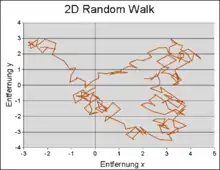
Одновимірне дискретне випадкове блукання — це випадковий процес $\{Y_{n}\}_{n\geq 0}$ з дискретним часом, який має вигляд: $Y_{n}=Y_{0}+\sum \limits _{i=1}^{n}X_{i}$ , де

$Y_{0}$ — початковий стан;
$X_{i}={\begin{cases}1,&p_{i}\\-1,&q_{i}\equiv 1-p_{i}\end{cases}},\quad 0<p_{i}<1,\quad i\in \mathbb {N}$ ;
випадкові величини $Y_{0},X_{i},i=1,2,\ldots$ спільно незалежні.

Випадкове блукання як ланцюг Маркова

Одномірне дискретне випадкове блукання є ланцюгом Маркова з цілими станами, чий початковий розподіл задається функцією ймовірності випадкової величини $X_{0}$ , а матриця перехідних ймовірностей має вигляд

P\equiv (p_{ij})_{i,j\in \mathbb {Z} }=\left({\begin{matrix}\ddots &\ddots &\ddots &\\&q_{-1}&0&p_{-1}&\\&&q_{0}&0&p_{0}\\&&&q_{1}&0&p_{1}\\&&&&\ddots &\ddots &\ddots \end{matrix}}\right)

,

тобто

p_{i,i+1}\equiv \mathbb {P} (X_{n+1}=i+1\mid X_{n}=i)=p_{i},

p_{i,i-1}\equiv \mathbb {P} (X_{n+1}=i-1\mid X_{n}=i)=q_{i},\quad i\in \mathbb {Z} ,

p_{ij}\equiv \mathbb {P} (X_{n+1}=j\mid X_{n}=i)=0,\quad |i-j|\not =1.

Теорема Донскера

Розглянемо випадкове блукання $Y_{n}=\sum \limits _{i=1}^{n}{X_{i}}$ , где $EX_{i}=0,DX_{i}=\sigma ^{2}<\infty$ .

Центральна гранична теорема стверджує, що ${\frac {Y_{n}}{\sigma {\sqrt {n}}}}\rightarrow N(0,1),n\rightarrow \infty$ за розподілом

Однак, у разі випадкових блукань, це твердження можна значно підсилити.

Побудуємо за $Y_{n}$ випадковий процес $S_{n}(t),t\in [0,1]$ , визначивши його так: $S_{n}\left({\frac {k}{n}}\right)={\frac {Y_{k}}{\sigma {\sqrt {n}}}}$ , а при інших t ми довизначимо процес лінійним продовженням:

$S_{n}(t)=(k+1-nt)S_{n}\left({\frac {k}{n}}\right)+(nt-k)S_{n}\left({\frac {k+1}{n}}\right),t\in \left({\frac {k}{n}},{\frac {k+1}{n}}\right)$

З центральної граничної теореми $\forall t$ $S_{n}(t)\rightarrow N(0,t),n\rightarrow \infty$ за розподілом

Це означає збіжність одновимірних розподілів процесу $S_{n}(t)$ до одновимірних розподілів вінерівського процесу. Теорема Донскера, звана також принципом інваріантності, стверджує, що має місце слабка збіжність процесів, $S_{n}(t)\rightarrow W(t),n\rightarrow \infty$

Слабка збіжність процесів означає збіжність неперервних за вінерівською мірою функціоналів, тобто дозволяє розраховувати значення функціоналів від броунівського руху (наприклад максимуму, мінімуму, останнього нуля, моменту першого досягнення рівня та інших) граничним переходом від простого випадкового блукання.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.