Функціонал

Відображення

${\displaystyle x_{0}\rightarrow f(x_{0})}$

є функцією, де ${\displaystyle x_{0}}$ є аргументом функції ${\displaystyle f}$. У той же час відображення функції у значення функції в точці

${\displaystyle f\rightarrow f(x_{0})}$

є функціоналом, тут ${\displaystyle x_{0}}$ — параметр.

За умови, що ${\displaystyle f}$ — лінійна функція з векторного простору на скалярне поле, вищевказані лінійні відображення є дуальними один одному, і в функціональному аналізі ці відображення називаються лінійними функціоналами.

Інтеграли, такі як

${\displaystyle f\rightarrow I[f]=\int _{\Omega }H(f(x),f'(x),\dots )\mu ({\rm {d}}x),}$

формують особливий клас функціоналів. Вони відображають функцію ${\displaystyle f}$ у простір дійсних чисел при умові, що функція ${\displaystyle H}$ є дійснозначною.

Приклади включають:

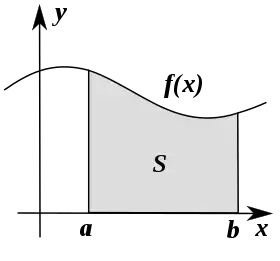
• площа під графіком додатньо визначеної функції ${\displaystyle f}$

${\displaystyle f\rightarrow \int _{x_{0}}^{x_{1}}f(x)\,{\rm {d}}x;}$

• ${\displaystyle L^{p}}$ норма функції на множині ${\displaystyle E}$

${\displaystyle f\rightarrow \left(\int _{E}|f|^{p}\,{\rm {d}}x\right)^{\frac {1}{p}};}$

• довжина дуги кривої у двовимірному евклідовому просторі

${\displaystyle \int _{x_{0}}^{x_{1}}{\sqrt {1+|f'|^{2}}}\,{\rm {d}}x.}$

Нехай ${\displaystyle X}$ — предгільбертів простір, ${\displaystyle {\vec {x}}\in X}$ — фіксований вектор, тоді відображення ${\displaystyle {\vec {y}}\rightarrow {\vec {x}}\cdot {\vec {y}}}$ є лінійним функціоналом на просторі ${\displaystyle X}$. Набір векторів ${\displaystyle {\vec {y}}}$ такий, що ${\displaystyle {\vec {x}}\cdot {\vec {y}}=0}$, є векторним підпростором простору ${\displaystyle X}$, який називається нуль-простором або ядром функціоналу, або ортогональним доповненням ${\displaystyle {\vec {x}}}$, що позначається як ${\displaystyle {\vec {x}}^{\perp }}$.

Наприклад, скалярний добуток з фіксованою функцією ${\displaystyle g\in L^{2}([-\pi ,\pi ])}$ визначає (лінійний) функціонал на гільбертовому просторі ${\displaystyle L^{2}([-\pi ,\pi ])}$ квадратично інтегровних функцій на відрізку ${\displaystyle [-\pi ,\pi ]}$:

${\displaystyle f\rightarrow \langle f,g\rangle =\int _{-\pi }^{\pi }fg\,{\rm {d}}x.}$

Якщо значення функціоналу можна обчислити для невеликих сегментів заданої кривої, а потім підсумувати, щоб знайти загальне значення, то у цьому випадку функціонал називається локальним. В іншому випадку функціонал називається нелокальним. Наприклад, функціонал

${\displaystyle F(y)=\int _{x_{0}}^{x_{1}}y(x)\,{\rm {d}}x}$

є локальним, а функціонал

${\displaystyle F(x)={\frac {\displaystyle \int _{x_{0}}^{x_{1}}y(x)\,{\rm {d}}x}{\displaystyle \int _{x_{0}}^{x_{1}}\left(1+(y(x))^{2}\right)\,{\rm {d}}x}}}$

є нелокальним. Зазвичай, це трапляється тоді, коли інтеграли зустрічаються окремо в чисельнику та знаменнику рівняння. Наприклад, при розрахунках центру мас.