Вихор Мерсенна

Вихор Мерсенна є витковим регістром зсуву з узагальненою віддачею (TGFSR)[1] (англ. twisted generalised feedback shift register). «Вихор» — це перетворення, яке забезпечує рівномірний розподіл генерованих псевдовипадкових чисел у 623 вимірах (для лінійних конгруентних генераторів його обмежено 5 вимірами). Тому функція кореляції між двома послідовностями вибірок у вихідній послідовності вихору Мерсенна мізерно мала.

Псевдовипадкова послідовність, породжена вихором Мерсенна, має дуже великий період, рівний числу Мерсенна, чого більш ніж достатньо для багатьох практичних застосувань.

Існують ефективні реалізації вихору Мерсенна, що перевершують за швидкістю багато стандартних ГПВЧ (зокрема, в 2-3 рази швидше від лінійних конгруентних генераторів). Алгоритм вихору Мерсенна реалізовано в програмній бібліотеці Boost[2], Glib[3] і стандартних бібліотеках для C++, Python[4][5][6], Ruby[7], R[8], PHP[9], MATLAB[10], Autoit[11].

Видавані вихором Мерсенна послідовності псевдовипадкових чисел успішно проходять статистичні тести Diehard, що підтверджує їхні хороші статистичні властивості.

Генератор не призначений для отримання криптографічно стійких випадкових послідовностей чисел. Для забезпечення криптостійкості вихідну послідовність генератора слід обробити одним із криптографічних алгоритмів хешування[12].

Запропоновано багато генераторів можливо «високої якості», але тільки деякі можна використати для серйозного моделювання через відсутність чіткого поняття «хаотичності» для генераторів псевдовипадкових чисел, оскільки кожен дослідник концентрується на конкретних параметрах хаотичності. Серед багатьох відомих мір, тести, засновані на вищому рівномірному розподілі, такі як спектральний тест і тест на k-розподілі, описаний нижче, вважаються найсильнішими.

x позначатимемо w-вимірні вектори над полем ${\displaystyle F_{2}}$ = {0,1}, відповідні машинним словам розміру w. Вихор Мерсенна генерує послідовність векторів, які є псевдовипадковими цілими з діапазону від 0 до 2^w — 1. Діленням на 2^w — 1 можна також отримати псевдовипадкове дійсне число з діапазону [0,1].

Алгоритм ґрунтується на такій рекурентній формулі:

${\displaystyle x_{k+n}:=x_{k+m}\oplus ({x_{k}}^{u}\mid {x_{k+1}}^{l})A,\qquad k=0,1,\ldots \qquad (1)}$

де:

• n — ціле, яке позначає порядок рекурентності,
• m — ціле, 1 ≤ m < n,
• A — матриця розміру w×w, з елементами з ${\displaystyle F_{2}}$,
• ${\displaystyle \mid }$ — побітове АБО (OR),
• ${\displaystyle \oplus }$ — додавання за модулем два (XOR).

У правій частині x_k^u позначає «старші w-r біт» x_k і x_k+1^l «молодші r біт» x_k+1. Вектор (x_k^u | x_k+1^l) є конкатенацією старших w-r біт x_k і молодших r біт x_k+1. Взявши (x₀, x₁,…, x_n-1) для початкового заповнення. Тоді генератор обчислить x_n за рекурентним виразом при k= 0. Для k = 1,2,…, генератор обчислить x_n+1, x_n+2,… Форму матриці A обрано з розрахунку швидкості виконання множення на A:

${\displaystyle A={\begin{pmatrix}0&1&&&&\\0&0&1&&&\\0&\cdots &\cdots &\ddots &&\\&&&&\ddots &\\&&&&&1\\a_{w-1}&a_{w-2}&\cdots &\cdots &\cdots &a_{0}\end{pmatrix}}}$

І обчислення xA зводиться до побітових операцій:

${\displaystyle {\boldsymbol {x}}A={\begin{cases}{\boldsymbol {x}}\gg 1&x_{0}=0\\({\boldsymbol {x}}\gg 1)\oplus {\boldsymbol {a}}&x_{0}=1\end{cases}}}$

де

${\displaystyle {\boldsymbol {x}}:=({x_{k}}^{u}\mid {x_{k+1}}^{l})\qquad \qquad k=0,1,\ldots }$

${\displaystyle {\boldsymbol {a}}:=({a_{w-1}},{a_{w-2}},\ldots ,{a_{0}})}$

${\displaystyle {\boldsymbol {x}}:=({x_{w-1}},{x_{w-2}},\ldots ,{x_{0}})}$

Неповні масиви

Неповні масиви

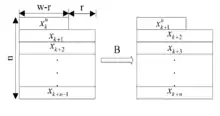
Послідовність МТ (x_k+n, x_k+n-1,…, x_k+1^u) утворює (n × w — r)-масив. Оскільки r бітів відкидаються, масив називають неповним масивом. Кожен елемент отримано з рекурентного співвідношення (1). Зміна стану MT також відбувається за лінійним співвідношенням і визначається за допомогою лінійного перетворення B.

Відповідно до загальної теорії лінійних рекурентних послідовностей, кожне значення в (n × w − r)-масиві є лінійною рекурентною послідовністю, що відповідає характеристичному многочлену φ_B(t) перетворення B. Матриця B має розміри (n × w − r) × (n × w − r) і таку форму:

${\displaystyle B={\begin{pmatrix}0&I_{w}&\cdots &0&0\\\vdots &&&&\\I_{w}&\vdots &\ddots &\vdots &\vdots \\\vdots &&&&\\0&0&\cdots &I_{w}&0\\0&0&\cdots &0&I_{w-r}\\S&0&\cdots &0&0\end{pmatrix}}{\begin{matrix}\\\\\leftarrow m{\hbox{-th row}}\\\\\\\\\end{matrix}}}$

${\displaystyle S={\begin{pmatrix}0&I_{r}\\I_{w-r}&0\end{pmatrix}}A}$

де ${\displaystyle I_{r}}$ — одинична матриця розміру r × r.

Для ${\displaystyle l=0,1,\ldots }$ виконується ${\displaystyle (x_{l+n},x_{l+n-1},\ldots ,x_{l+1}):=(x_{l+n-1},x_{l+n-2},\ldots ,x_{l})B}$.Характеристичний многочлен φ_B(t) перетворення B має вигляд:

${\displaystyle \Phi _{B}(t)=(t^{n}+t^{m})^{w-r}\cdot (t^{n-1}+t^{m-1})^{r}+a_{0}(t^{n}+t^{m})^{w-r}\cdot (t^{n-1}+t^{m-1})^{r-1}+...+a_{r-2}(t^{n}+t^{m})^{w-r}\cdot (t^{n-1}+t^{m-1})+a_{r-1}(t^{n}+t^{m})^{w-r}+a_{r}(t^{n}+t^{m})^{w-r-1}+...+a_{w-2}(t^{n}+t^{m})+a_{w-1}}$

Послідовність досягає максимального періоду 2^(nw-r)−1, тоді і тільки тоді коли φ_B(t) — примітивний.

Вихор Мерсенна алгоритмічно реалізується двома основними частинами: рекурсивною і загартування. Рекурсивна частина являє собою регістр зсуву з лінійним зворотним зв'язком, у якому всі біти в його слові визначаються рекурсивно; потік вихідних бітів визначається також рекурсивно функцією бітів стану.

Блок-схема.

Регістр зсуву складається з 624 елементів, і, в цілому, з 19937 клітинок. Кожен елемент має довжину 32 біти за винятком першого елемента, який має тільки 1 біт завдяки відкиданню біта.

Процес генерування починається з логічного множення на бітову маску, що відкидає 31 біт (крім найбільш значущих).

Наступним кроком виконується ініціалізація (x₀, x₁,…, x₆₂₃) будь-якими беззнаковими 32-розрядними цілими числами. Наступні кроки включають об'єднання та перехідні стани.

Зміна стану МТ.

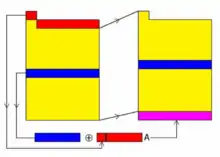
Простір станів має 19937 біт (624·32 — 31). Наступний стан генерується зсувом одного слова вертикально вгору і вставленням нового слова в кінець. Нове слово обчислюється гамуванням середньої частини з виключеною[14]. Вихідна послідовність починається з x₆₂₄, x₆₂₅,…

Алгоритм має шість етапів:

 Крок 0. Попередньо ініціалізується значення сталих u, h, a
 u ← 10…0   бітова маска старших w-r бітів,
 h ← 01…1   бітова маска молодших r бітів,
 a ← aw-1aw-2…a0  останній рядок матриці A.

 Крок 1. x[0], x[1],…,x[n-1] ←  початкове заповнення

 Крок 2. Обчислення (xiu | xi+1l)
 y ← (x[i] AND u1) OR (x[(i + 1) mod n] AND h1)

 Крок 3. Обчислюється значення наступного елемента послідовності за рекурентним виразом (1)
 x[i] ← x[(i + m) mod n] XOR (y>>1) XOR a   якщо молодший біт y = 1

 Або
 x[i] ← x[(i + m) mod n] XOR (y>>1) XOR 0   якщо молодший біт y = 0
 Крок 4. Обчислення x[i]T
 y ← x[i]
 y ← y XOR (y>>u)
 y ← y XOR ((y<<s) AND b)
 y ← y XOR ((y<<t) AND c)
 z ← y XOR (y>>l)
 виведення z
 Крок 5. i ← (i + 1) mod n 

 Крок 6. Перейти до кроку 2.

Параметри MT ретельно підібрано для досягнення згаданих вище властивостей. Параметри n і r вибрано так, що характеристичний многочлен примітивний або nw — r дорівнює числу Мерсенна 19937. Зверніть увагу, що значення w еквівалентне розміру слова комп'ютера. У цьому випадку це 32 біти. Тоді як значення n, m, r і w фіксуються, значення останнього рядка матриці A вибирається випадковим чином. Для чисел Мерсенна тест на простоту цілих значно простіший. Так, відомо багато простих чисел Мерсенна (тобто простих виду 2^p−1), до p=43112609 . Параметри загартування (англ. tempering) підібрано так, що ми можемо отримати хороший рівномірний розподіл. Всі параметри МТ наведено в таблиці 1.

У зв'язку зі змінами в технології, зокрема, зростанням продуктивності процесорів, винайдено 64-бітові і 128-бітові версії МТ. 64-розрядну версію запропонував 2000 року Такудзі Нісімура,[15] 128-розрядну — 2006 року[16][17] теж він. Обидві версії мають той самий період, що й оригінальний MT.

64-бітовий MT має дві версії. Перша версія використовує те саме рекурсивне співвідношення, в другу версію додано ще два вектори, що збільшило кількість членів характеристичного многочлена:

${\displaystyle x_{k+n}:=x_{k+m2}\oplus x_{k+m1}\oplus x_{k+m0}\oplus ({x_{k}}^{u}\mid {x_{k+1}}^{l})A\qquad (2)}$

Порівняно з 32-розрядною версією MT, 64-розрядна версія працює швидше. Всі параметри для 64-бітової версії наведено в таблиці 2.

• M. Matsumoto, T. Nishimura. Mersenne twister: A 623-dimensionally equidistributed uniform pseudorandom number generator // ACM Trans. on Modeling and Computer Simulations : journal. — 2017. — Vol. 8, no. 1 (23 January). — P. 3—30. — DOI:10.1145/272991.272995.
• Matsumoto, M.; Kurita, Y. Twisted GFSR generators // ACM Trans. on Modeling and Computer Simulations. — 1992. — Т. 2, № 3 (23 January). — С. 179—194. — DOI:10.1145/146382.146383.
• Matsumoto, Makoto; Nishimura, Takuji; Hagita, Mariko; Saito, Mutsuo. Cryptographic Mersenne Twister and Fubuki Stream/Block Cipher. — 2005. — 23 January.
• T. Nishimura. Tables of 64-bit Mersenne twisters // ACM Trans. on Modeling and Computer Simulations. — 2000. — Т. 10, № 4 (23 January). — С. 248—357. — DOI:10.1145/369534.369540.
• Matsumoto M., Saito M., Nishimura T., Hagita M. CryptMT Stream Cipher Ver. 3.The eSTREAM Project.

• Makoto Matsumoto, Academic publications on MT(англ.)
• Mersenne Twister home page, with C code(англ.)
• Cuba — a library for multidimensional numerical integration
• The Mersenne Twister(англ.)