Дискретний рівномірний розподіл

Дискретний рівномірний розподіл
	Масова функція розподілу імовірностей для рівномірного розподілу із параметром n = 5; n = 5 де n = b − a + 1
	Функція розподілу ймовірностей 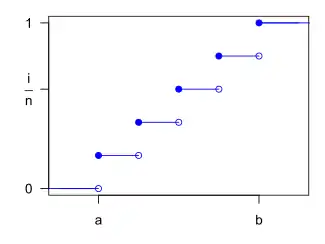Кумулятивна функція дискретного рівномірного розподілу для n = 5
Параметри	; ;
Носій функції
Розподіл імовірностей
Функція розподілу ймовірностей (cdf)
Середнє
Медіана
Мода	N/A
Дисперсія
Коефіцієнт асиметрії
Коефіцієнт ексцесу
Ентропія
Твірна функція моментів (mgf)
Характеристична функція

В теорії ймовірностей і статистиці випадкова величина має дискретний рівномірний розподіл, якщо вона приймає скінченне число значень з однаковими ймовірностями.

Якщо випадкова величина може приймати будь-яке з n значень k₁,k₂,…,k_n, тоді це є дискретним рівномірним розподілом. Ймовірність випадання k_j дорівнює 1/n. Простим прикладом дискретного рівномірного розподілу є випадання гральної кості. k набуває значень 1, 2, 3, 4, 5, 6 і кожен раз $k$ випадає з імовірністю 1/6. У випадку, коли випадкова величина є дійсним числом, то функцію розподілу можна виразити у термінах виродженого розподілу таким чином:

$F(k;a,b,n)={1 \over n}\sum _{i=1}^{n}H(k-k_{i})$

Визначення максимуму

Вибірка із k спостережень отримана із рівномірного розподілу цілих чисел $1,2,\dotsc ,N$ , для якої існує задача оцінити невідомий максимум N. Цю задачу іноді називають задачею про німецький танк, після того як цей метод оцінки максимуму було застосовано для оцінки темпів виробництва німецьких танків під час Другої світової війни.

Незміщена оцінка з мінімальною дисперсією для рівномірного розподілу, яка визначає максимум задається наступним чином

{\hat {N}}={\frac {k+1}{k}}m-1=m+{\frac {m}{k}}-1

де m є вибірковим максимумом, а k - розмір вибірки, для вибірки без повторного заміщення.[1] Цей приклад можна розглядати як спрощений випадок оцінки максимального інтервалу.

При цьому матимемо дисперсію[1]

{\frac {1}{k}}{\frac {(N-k)(N+1)}{(k+2)}}\approx {\frac {N^{2}}{k^{2}}}{\text{ для малих вибірок }}k\ll N

тож стандартне відхилення приблизно становить ${\tfrac {N}{k}}$ , середній розмір (для сукупності) проміжку між елементами; порівняємо із вищевказаним ${\tfrac {m}{k}}$ .

Максимум вибірки є оцінкою максимальної правдоподібності для максимуму сукупності, але, як зазначалося вище, він є зміщеним.

Якщо вибірка не представлена числами, але її можна промаркувати або розрізнити, розмір популяції можливо визначити методом "Зловити/повторити".

Виведення

Для будь-якого цілого числа m такого що k ≤ m ≤ N, імовірність того, що вибірковий максимум буде дорівнювати m можна розрахувати наступним чином. Кількість різних груп із k танків, які можуть бути утворені із загальної кількості з N танків визначається через біноміальний коефіцієнт ${\tbinom {N}{k}}$ . Оскільки при такому способі підрахунку, перестановки танків розраховуються лише раз, ми можемо впорядкувати серійні номери і відмітити максимальний з них в кожній вибірці. Аби розрахувати імовірність ми повинні полічити кількість впорядкованих вибірок, які можуть містити останній елемент, який буде дорівнювати m а всі інші k-1 танків мають номери менші або такий що дорівнює m-1. Кількість таких вибірок з k-1 танків які можна отримати із загальної кількості m-1 танків задається біноміальним коефіцієнтом ${\tbinom {m-1}{k-1}}$ , тож імовірність отримати максимум m становить $P(m)={\tbinom {m-1}{k-1}}{\big /}{\tbinom {N}{k}}$ .

Дано загальну кількість N і розмір вибірки k, математичне сподівання максимуму вибірки визначається як:

{\begin{aligned}\mu =\mathrm {E} [m]&=\sum _{m=k}^{N}m{\frac {\tbinom {m-1}{k-1}}{\tbinom {N}{k}}}\\&={\frac {1}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}{\frac {m!}{(m-k)!}}\\&={\frac {k!}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}{\tbinom {m}{k}}\\&=k{\frac {\tbinom {N+1}{k+1}}{\tbinom {N}{k}}}\\&={\frac {k(N+1)}{k+1}},\end{aligned}}

де було використано рівняння із трикутником Паскаля $\sum _{m=k}^{N}{\tbinom {m}{k}}={\tbinom {N+1}{k+1}}$ .

Із цього рівняння, невідому кількість N можна розрахувати через сподівання і розмір вибірки, наступним чином

{\begin{aligned}N&=\mu \left(1+k^{-1}\right)-1.\end{aligned}}

Відповідно до лінійності математичного сподівання, отримаємо

{\begin{aligned}\mu \left(1+k^{-1}\right)-1&=\mathrm {E} \left[m\left(1+k^{-1}\right)-1\right],\end{aligned}}

і таким чином незміщена оцінка для N отримується за допомогою заміни сподівання на спостереження,

{\begin{aligned}{\hat {N}}&=m\left(1+k^{-1}\right)-1.\end{aligned}}

Крім того, що ця оцінка є незміщеною вона також досягає мінімальної дисперсії. Аби показати це, відмітимо спершу, що максимум вибірки є достатньою статистикою для визначення максимуму сукупності, оскільки імовірність P(m;N) задається як функція лише від однієї m. Далі необхідно довести, що статистика m також є повною статистикою, особливим видом достатньої статистики (demonstration pending). Тоді Теорема Лемана-Шеффе передбачає, що ${\hat {N}}$ є незміщеною оцінкою для N із найменшою дисперсією.[2]

Дисперсія оцінки розраховується як дисперсія вибіркового максимуму

{\begin{aligned}\mathrm {Var} [{\hat {N}}]&={\frac {(k+1)^{2}}{k^{2}}}\mathrm {Var} [m].\end{aligned}}

Дисперсія максимуму в свою чергу розраховується із математичних сподівань $m$ і $m^{2}$ . Розрахунок математичного сподівання для $m^{2}$ є наступним,

{\begin{aligned}\mathrm {E} [m^{2}]&=\sum _{m=k}^{N}m^{2}{\frac {\tbinom {m-1}{k-1}}{\tbinom {N}{k}}}\\&={\frac {1}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}m{\frac {m!}{(m-k)!}}\\&={\frac {1}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}(m+1-1){\frac {m!}{(m-k)!}}\\&={\frac {1}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}{\frac {(m+1)!}{(m-k)!}}-{\frac {1}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}{\frac {m!}{(m-k)!}}\end{aligned}}

де другий терм є математичним сподіванням для $m$ . Перший терм можна виразити через k і N,

{\begin{aligned}{\frac {1}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}{\frac {(m+1)!}{(m-k)!}}&={\frac {(k+1)!}{(k-1)!{\tbinom {N}{k}}}}\sum _{m=k}^{N}{\tbinom {m+1}{k+1}}\\&={\frac {k(k+1)}{\tbinom {N}{k}}}\sum _{n=k+1}^{N+1}{\tbinom {n}{k+1}}\\&={\frac {k(k+1)}{\tbinom {N}{k}}}{\tbinom {N+2}{k+2}}\\&={\frac {k(N+2)(N+1)}{(k+2)}}\end{aligned}}

де була використана заміна $n=m+1$ і використане рівняння із трикутником Паскаля. Підставлення цього результату і математичного сподівання $m$ в рівняння для $E[m^{2}]$ дає

{\begin{aligned}\mathrm {E} [m^{2}]&={\frac {k(N+2)(N+1)}{(k+2)}}-{\frac {k(N+1)}{k+1}}\\&=k(N+1){\Big (}{\frac {N+2}{k+2}}-{\frac {1}{k+1}}{\Big )}\\&={\frac {k(N+1)(kN+k+N)}{(k+1)(k+2)}}\end{aligned}}

Тоді можна отримати дисперсію для $m$ ,

{\begin{aligned}\mathrm {Var} [m]&=\mathrm {E} [m^{2}]-\mathrm {E} [m]^{2}\\&={\frac {k(N+1)}{(k+1)}}{\Big (}{\frac {kN+k+N}{k+2}}-{\frac {k(N+1)}{k+1}}{\Big )}\\&={\frac {k(N+1)}{(k+1)}}{\frac {(N-k)}{(k+2)(k+1)}}\\&={\frac {k(N+1)(N-k)}{(k+1)^{2}(k+2)}}\end{aligned}}

Зрештою можна розрахувати дисперсію для оцінки ${\hat {N}}$ ,

{\begin{aligned}\mathrm {Var} [{\hat {N}}]&={\frac {(k+1)^{2}}{k^{2}}}\mathrm {Var} [m]\\&={\frac {(k+1)^{2}}{k^{2}}}{\frac {k(N+1)(N-k)}{(k+1)^{2}(k+2)}}\\&={\frac {(N+1)(N-k)}{k(k+2)}}.\end{aligned}}

Примітки

Johnson, Roger (1994). Estimating the Size of a Population. Teaching Statistics 16 (2 (Summer)). doi:10.1111/j.1467-9639.1994.tb00688.x. Архів оригіналу за 26 травня 2009. Процитовано 18 березня 2019.
G. A. Young and R. L Smith (2005) Essentials of Statistical Inference, Cambridge University Press, Cambridge, UK, p. 95

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[Johnson-1] Johnson, Roger (1994). Estimating the Size of a Population. Teaching Statistics 16 (2 (Summer)). doi:10.1111/j.1467-9639.1994.tb00688.x. Архів оригіналу за 26 травня 2009. Процитовано 18 березня 2019.

[2] G. A. Young and R. L Smith (2005) Essentials of Statistical Inference, Cambridge University Press, Cambridge, UK, p. 95