Відстань Гаусдорфа

Складові обчислення відстані Гаусдорфа між зеленою лінією X і голубою лінією Y

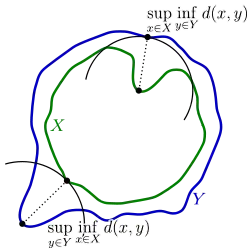
Нехай ${\displaystyle X}$ і ${\displaystyle Y}$ дві замкнені обмежені підмножини метричного простору ${\displaystyle M}$ тоді відстань за Гаусдорфом, ${\displaystyle d_{H}(X,\;Y)}$, між ${\displaystyle X}$ та ${\displaystyle Y}$ є мінімальне число ${\displaystyle r}$ таке, що замкнутий ${\displaystyle r}$-окіл ${\displaystyle X}$ містить ${\displaystyle Y}$ і також замкнутий ${\displaystyle r}$-окіл ${\displaystyle Y}$ містить ${\displaystyle X}$.

Іншими словами, якщо ${\displaystyle |xy|}$ позначає відстань між точками ${\displaystyle x}$ та ${\displaystyle y}$ в ${\displaystyle M}$, то

${\displaystyle d_{H}(X,\;Y)=\max \left\{\sup _{x\in X}\inf _{y\in Y}|xy|,\;\sup _{y\in Y}\inf _{x\in X}|xy|\right\}.}$

Нехай ${\displaystyle F(M)}$ позначає множину всіх непорожніх компактних підмножин метричного простору ${\displaystyle M}$ з відстанню Гаусдорфа:

• Топологія простору ${\displaystyle F(M)}$ повністю визначається топологією ${\displaystyle M}$.
• (Теорема Бляшке) ${\displaystyle F(M)}$ компактно тоді і тільки тоді, коли компактно ${\displaystyle M}$.
• ${\displaystyle F(M)}$ повно тоді і тільки тоді, коли ${\displaystyle M}$ повне.

• Іноді відстань Гаусдорфа розглядається на множині всіх замкнутих підмножин метричного простору, в цьому випадку відстань між деякими підмножинами може дорівнювати нескінченності.
• Іноді відстань Гаусдорфа розглядається на множині всіх підмножин метричного простору. У цьому випадку вона є тільки псевдовідстанню і не є відстанню, так як «відстань» між різними підмножинами може дорівнювати нулю.
• В евклідовій геометрії, часто застосовується відстань Гаусдорфа з точністю до конгруентності. Нехай ${\displaystyle X}$ та ${\displaystyle Y}$ дві компактні підмножини евклідового простору, тоді ${\displaystyle D_{H}(X,\;Y)}$ визначається як мінімум ${\displaystyle d_{H}(I(X),\;Y)}$ за всіма рухами евклідового простору ${\displaystyle I}$. Строго кажучи, ця відстань на просторі класів конгруентності компактних підмножин евклідового простору.
• Відстань Громова-Гаусдорфа аналогічна відстані Гаусдорфа з точністю до конгруентності. Вона перетворює множину (ізометричних класів) компактних метричних просторів в метричний простір.

• Бляшке, Круг и шар, М.: Наука, 1967
• Скворцов В. А. Примеры метрических пространств // Библиотека «Математическое просвещение». — 2001. — Выпуск 9.
• Хаусдорф «Теория множеств»