Гармонійна четвірка

Гармонійна четвірка точок — четвірка точок на проєктивній прямій, подвійне відношення яких $(ABCD)=-1$ . В цьому випадку кажуть також, що точки $C$ і $D$ гармонійно поєднані відносно $A,B$ і пишуть $H(AB,CD)$ .

Приклад гармонійної четвірки точок A, B, C і D.

Гармонійна четвірка прямих — четвірка прямих $a,b,c,d$ у проєктивній площині, що проходять через одну точку $S$ , для яких будь-яка четвірка точок $A,B,C,D$ , така, що $A\in a,B\in b,C\in c,D\in d$ , що знаходяться на одній прямій, є гармонійною. В цьому випадку пишуть $H(ab,cd)$ .

Властивості

Якщо гармонійну четвірку прямих перетинає пряма, то на цій прямій утворюється гармонійна четвірка точок.
На кожній стороні повного чотиривершинника є гармонійна четвірка точок.
На кожній діагоналі повного чотиривершинника є гармонійна четвірка точок.

Побудова

A, B, C, D — гармонійна четвірка точок.

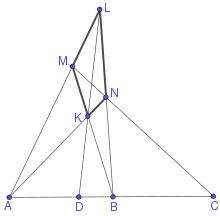
Для будь-яких трьох точок, що лежать на одній прямій, користуючись гармонійними властивостями повного четиривершинника, можна побудувати четверту точку так, що вийде гармонійна четвірка точок. А саме, точки перетину поротилежних сторін повного чотиривершинника і точки перетину діагоналей з прямою, що проходить через ці точки, утворюють гармонійну четвірку точок.

Гармонійна четвірка на розширеній евклідовій площині

Якщо точка $D_{\infty }$ невласна, то четвірка $A,B,C,D_{\infty }$ є гармонійною, якщо $C$ — середина відрізка $AB$ .
Якщо $ABCD$ — повний чотиривершинник і його діагональні точки $P_{\infty },Q_{\infty }$ — невласні, то на розширеній евклідовій площині $ABCD$ — паралелограм, а з його гармонійних властивостей випливає, що точка перетину його діагоналей ділить їх навпіл.
Якщо $ABCD$ — повний чотиривершинник, у якого одна діагональна точка $R_{\infty }=BC\cap AD$ — невласна, $P=AB\cap CD,Q=AC\cap BD$ , то на розширеній евклідовій площині $ABCD$ — трапеція, а з його гармонійних властивостей випливає, що $PQ$ ділить $AD$ навпіл.

Див. також

Відношення напрямлених відрізків

Література

Базылев, Дуничев, Иваницкая. Геометрия, часть 2. — М. : Просвещение, 1975.
Ефимов Н. В. Высшая геометрия. — 6-е изд.. — М., 1978.
Певзнер С.Л. Проективная геометрия. — М. : Просвещение, 1980.
Постников М. М. Аналитическая геометрия. — 1973.
Х. С. М. Кокстер. Действительная проективная плоскость / под ред. проф. А. А. Глаголева — М., 1959.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.