Повний чотирикутник

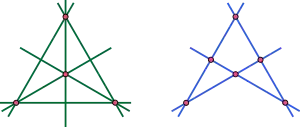
Фігура, що складається з чотирьох точок на площині, ніякі три з яких не колінеарні, і шести прямих, що попарно їх з'єднують, називається повним чотирикутником. Сторони, які не мають спільної вершини в повному чотирикутнику, називаються протилежними. Точки перетину трьох пар протилежних сторін називаються діагональними точками[3].

Фігура, що складається з чотирьох прямих на площині, ніякі три з яких не сходяться в одній точці, і шести точок попарного їх перетину, називається повним чотирибічником. Чотири прямі називаються сторонами, а шість точок — вершинами чотирибічника. Вершини, що не примикають до однієї сторони, називаються протилежними. Прямі, що з'єднують три пари протилежних вершин, називаються діагоналями[3].

Ряд з шести (п'яти, чотирьох) точок, у яких сторони повного чотирикутника перетинають деяку пряму, називається рядом точок, породженим повним чотирикутником[4]. Якщо така пряма проходить через дві діагональні точки A і C, а B і D — точки, в яких дві інші сторони перетинають пряму AC, то пари точок AC і BD називаються гармонійною четвіркою і позначаються H (AC, BD). Точки B і D називаються гармонійними відносно A і C, а точка D (або B) називається гармонійно поєднаною з точкою B (або D) відносно пари точок A і D[5].

Якщо між точками двох фігур існує відповідність, така, що прямі, які з'єднують кожну пару відповідних точок, сходяться в деякій точці O, то фігури називаються перспективними відносно центра O [3].

Якщо між прямими лініями двох фігур існує відповідність, така, що точки перетину кожної пари відповідних прямих лежать на одній прямій l, то ці фігури називаються перспективними відносно осі l.

Після відкриття площини Фано, скінченної геометрії, в якій діагональні точки повного чотирикутника колінеарні, деякі автори додають до аксіом проєктивної геометрії аксіому Фано, яка постулює, що діагональні точки не колінеарні[6][7].

KLMN є повним чотирикутником. Точка D є проєктивно гармонійно поєднаною з точкою C

Як система точок і прямих, в якій всі точки належать однаковому числу прямих, а всі прямі містять однакове число точок, повний чотирикутник і повний чотирибічник є проєктивними конфігураціями. В позначеннях проєктивних конфігурацій повний чотирикутник записується як (4₃6₂), а повний чотирибічник — як (6₂4_3), де числа вказують кількість точок, кількість прямих, що проходять через кожну точку, кількість прямих і кількість точок на кожній прямій. Проєктивно двоїстою конфігурацією повного чотирикутника є повний чотирибічник, і навпаки. Для будь-яких двох повних чотирикутників або будь-яких двох повних чотирибічників є єдине проєктивне перетворення, що переводить одну з конфігурацій в іншу[8].

Карл Штаудт перетворив основи математики 1847 року, використовуючи повний чотирикутник, коли він помітив, що «властивості гармонійності» ґрунтуються на супутніх властивостях чотирикутника — точки перетину протилежних сторін чотирикутника і перетину діагоналей з прямою, що проходить через ці точки, утворюють гармонійну четвірку. Дослідники сучасної геометрії та алгебри звернули увагу на вплив Штаудта на Маріо П'єрі та Фелікса Кляйна.

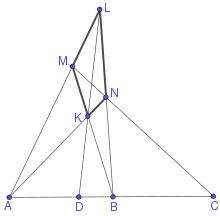
Девід Велз (David Wells)[9] описує деякі додаткові властивості повних чотирибічників, у яких використовуються метричні властивості евклідової площини, які не є чисто проєктивними. Середини діагоналей колінеарні і (як довів Ісаак Ньютон) на тій самій прямій лежить центр конічного перетину, дотичного до чотирьох прямих чотирибічника. Будь-які три прямі чотирибічника утворюють сторони трикутника. Ортоцентри чотирьох трикутників, утворених таким чином, лежать на інший прямій, перпендикулярній до першої прямої (що проходить через середини діагоналей). Описані кола цих чотирьох трикутників перетинаються в одній точці. Крім того, три кола, побудовані на діагоналях як на діаметрах, належать одному пучку кіл[10], вісь якого проходить через ортоцентри.

Полярні кола трикутників повного чотирибічника утворюють систему коаксіальних кіл[11].

• Пряма Ньютона
• Коніка дев'яти точок
• Чотирикутник

• Дж. В. Юнг. Проективная геометрия. — Москва : Государственное издательство ИНОСТРАННОЙ ЛИТЕРАТУРЫ, 1949.
• Roger A. Johnson. Advanced Euclidean Geometry. — Mineola, New York : Dover Publications, 2007. — ISBN 978-0-486-46237-0. (Первоначальная публикация — 1960)
• H. S. M. Coxeter. Projective Geometry, 2nd ed.. — Springer-Verlag, 1987. — ISBN 0-387-96532-7.
• Robin Hartshorne. Foundations of Projective Geometry. — W. A. Benjamin, 1967. — С. 53–6.
• Robert Lachlan. An Elementary Treatise on Modern Pure Geometry. — London, New York : Macmillan and Co., 1893. Посилання з Історичних математичних монографій Корнелльського університету
• David Wells. The Penguin Dictionary of Curious and Interesting Geometry. — Penguin, 1991. — С. 35–36. — ISBN 0-14-011813-6.

• Hazewinkel, Michiel, ред. (2001). Quadrangle, complete. Encyclopedia of Mathematics. Springer. ISBN 978-1-55608-010-4.
• Bogomolny, Alexander. The Complete Quadrilateral. Cut-the-Knot.
• Weisstein, Eric W. Complete Quadrangle(англ.) на сайті Wolfram MathWorld.