Геометричні характеристики перерізів
Геометри́чні характери́стики пере́різів — числові величини (параметри), що визначають розміри, форму, розташування поперечного перерізу однорідного за пружними властивостями деформівного елемента конструкції і, як наслідок, характеризують опір цього елемента різним видам деформації.
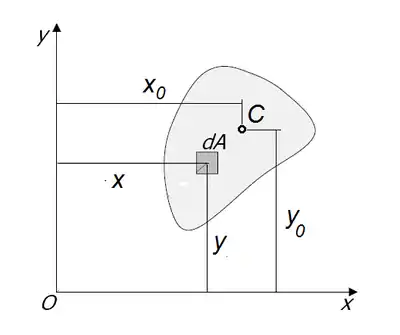
Площа поперечного перерізу
Розглянемо довільний поперечний переріз. Виділимо нескінченно малий елемент dA, положення якого в прямокутній системі координат визначається величинами x і y. У загальному випадку площа поперечного перерізу визначається у вигляді
Ця величина завжди додатна, має розмірність довжини в другій степені і виміряється у м², см², мм². Площа поперечного перерізу бруса є геометричною характеристикою його міцності й жорсткості не завжди, а лише при рівномірному розподілі механічних напружень у поперечному перерізі. При нерівномірному розподілі напружень, що має місце при роботі бруса в умовах кручення, його міцність і механічна жорсткість залежать уже від інших геометричних характеристик.
Статичний момент плоскої фігури
Статичний момент плоскої фігури (англ. First moment of area) відносно осі х або у дорівнює добутку усієї площі фігури на відстань від її центру ваги до цієї осі.
Розглянемо переріз у довільній декартовій прямокутній системі координат xOy. Виберемо елемент площі dA. Тоді величина
буде називатися статичним моментом площі A відносно осі х.
Аналогічно — статичний момент цієї площі відносно осі y.
Розмірність статичних моментів площі — одиниці довжини в третьому степені (м³, см³). Статичні моменти площі можуть бути додатними, від'ємними та рівними нулю.
Координати центра тяжіння
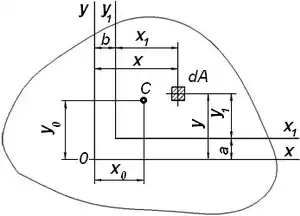
Розглянемо той же переріз при паралельному переносі осей x1 = x — b; y1 = y — a. За визначенням:
Очевидно, що величини a і b можуть набувати довільних значень. Виберемо їх так, щоб виконувалися умови
- ,
Тоді, , , і осі x1, y1 називаються центральними осями, а точка їх перетину — центром тяжіння (ваги) перерізу. Отже, положення центра тяжіння перерізну (точка C) визначається виразами
- , ,
Для випадків, коли переріз може бути розбитий на прості складові частини, площі й координати центрів тяжіння яких відомі, положення центра тяжіння всього перерізу визначають за формулами:
- ,
- .
Моменти інерції плоских перерізів
Моменти інерції плоских перерізів (англ. Second moment of area або англ. second moment of inertia). Розрізняють такі види моментів інерції плоских перерізів (фігур).
Осьовий момент інерції
Осьовий момент інерції відносно розглянутої осі — сума добутків елементарних площ dA на квадрат їх відстаней до цієї осі, взята по всій площі перерізу A.
Полярний момент інерції
Полярний момент інерції відносно даної точки — сума добутків елементарних площ dA на квадрати їх відстаней До цієї точки, взята по всій площі перерізу A:
Відцентровий момент інерції
Відцентровий момент інерції відносно осей координат — сума добутків елементарних площ dA на їх відстані до цих осей, взята по всій площі перерізу A:
Відцентровий момент інерції мають розмірність м4 і може бути додатнім, від'ємним і рівним нулю. Осі, відносно яких відцентровий момент інерції дорівнює нулю, називаються головними центральними осями.
Момент опору
Осьовий момент опору
Осьовий момент опору відносно заданої осі — величина рівна моменту інерції відносно тієї ж осі віднесеному до відстані до найвіддаленішої від цієї осі точки перерізу:
- ;
- .
Полярний момент опору
Полярний момент опору аналогічно обчислюється за формулою:
- ,
де — радіус розташування найвіддаленішої від осі кручення точки перерізу.
Радіус інерції
Момент інерції фігури відносно довільної осі можна представити у вигляді добутку площі фігури на квадрат величини, яку називають радіусом інерції:
де — радіус інерції відносно осі x. Тоді:
Джерела
- Опір матеріалів. Підручник /Г. С. Писаренко, О. Л. Квітка, Е. С. Уманський. За ред. Г. С. Писаренка — К.: Вища школа,1993. — 655 с. ISBN 5-11-004083-4
- Мильніков О. В. Опір матеріалів. Конспект лекцій. — Тернопіль: Видавництво ТНТУ, 2010. — 257 с.
