Піднесення до степеня

Підне́сення до сте́пеня — бінарна операція, записується як $\ a^{n},$ для основи степеня $\ a$ та показника степеня $\ n,$ в результаті застосування отримується степінь.[1]

Результати обчислення
Додавання (+)
1-й доданок + 2-й доданок =	сума
Віднімання (−)
зменшуване − від'ємник =	різниця
Множення (×)
1-й множник × 2-й множник =	добуток
Ділення (÷)
ділене ÷ дільник =	частка
Ділення з остачею (mod)
ділене mod дільник =	остача
Піднесення до степеня
основа степеня^{показник степеня} =	степінь
Обчислення кореня (√)
$показник кореня \sqrt підкореневий вираз$ =	корінь
Логарифм (log)
log_основа(число) =	логарифм

Графік функції

y = b x

для різних значень основи b: для 10 (зеленим), для основи e (червоним), для 2 (синім), і 12 (блакитним). Кожна крива проходить через точку

(0, 1)

оскільки, будь-яке число піднесене до степеня 0 дасть значення 1. При

x = 1

, значення y дорівнює основі, оскільки будь-яке число піднесене до степеня 1 є самим числом.

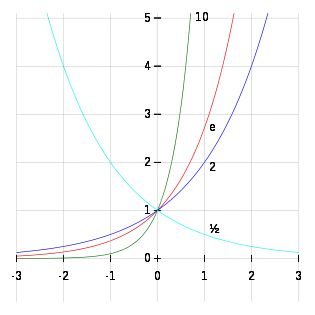
Якщо n — натуральне число, піднесення до степеня відповідає n-кратному множенню:

a^{n}=\underbrace {a\times \cdots \times a} _{n}.

Подібно до того, як множення на ціле число відповідає багатократному додаванню:

a\times n=\underbrace {a+\cdots +a} _{n}.

.

Другий степінь називають інакше квадратом, третій степінь — кубом. Першим степенем числа називають саме число, наприклад 7¹ = 7^*.

Історія

Поняття степеня використовувалося давньогрецьким математиком Евклідом для дослідження квадрату прямої.[2] Архімед відкрив і довів закон для степенів — 10^a 10^b = 10^a+b, необхідний аби оперувати степенями числа 10[3]. У 9-му столітті, перський математик Аль-Хорезмі використовував терміни мал для квадрата і кахб для куба, які згодом ісламські математики представляли у вигляді математичної нотації як m і k, відповідно, як видно із роботи Аль Каласаді до 15-го століття,.[4]

У кінці 16-го століття, Йост Бургі для степенів використовував римські літери[5].

На початку 17-го століття, перша форма сучасного позначення степеня була запропонована Рене Декартом у своїй праці під назвою La Géométrie; де, у книзі I і було введено відповідні позначення.[6]

Деякі математики (наприклад, Ісаак Ньютон) використовували експоненти лише для степенів, що більші за двійку, для позначення квадрату вони віддавали перевагу використовувати множення із повторенням. Таким чином вони б записали поліноми, наприклад, як ax + bxx + cx³ + d.

Ніколас Шуке використовував форму показникового запису в 15-му столітті, яку згодом використали Геріх Грамматеус і Михаель Штифель у 16-му столітті. Слово «експонента» виникло в 1544 завдяки Михаелю Штифелю.[7] В 16-му столітті Роберт Рекорд використовував термін квадрат, куб, дзензизензик (четвертий степінь), сурсолід (п'ятий), дзензікуб (шостий), другий сурсолід (сьомий), і дзензизензензик (восьмий).[8] Також для назви четвертого степеня використовували слово біквадрат.

Інший синонім, що існував в історії, інволюція,[9] зараз є рідким і його не варто плутати із більш загальним значенням цього слова.

У 1748 Леонард Ейлер написав «розглянемо експоненти або степені, в яких сама експонента (показник) є змінною. Очевидно, що величини такого типу не є алгебраїчними функціями, оскільки в них показних мав би бути константою.»[10] Із цим введенням у трансцендентні функції, Ейлер заклав початок сучасному введенню в натуральний логарифм, що є оберненою функцією для y = e^x.

Для цілих показників

Нульовий показник

При піднесені до степеня 0 будь-якого ненульового числа результатом буде 1[11]:

b^{0}=1

Однією з інтерпретацій для пояснення такого випадку є уявлення про пустий добуток.

Більш спірним випадком є випадок 0⁰ — нуль в степені нуль.

Від'ємні показники

Наступне рівняння є справедливим для будь-якого довільного цілого числа n і не нульового x:

x^{-n}={\frac {1}{x^{n}}}

Піднесення числа 0 до від'ємного показника степеня вважають або не визначеним, або визначеним як нескінченність $\infty$ .

Приведена вище рівність може бути доведена із визначення, якщо продовжити значення показника у негативну область цілих чисел.

Для не нульових значень x і додатних n, рекурентна рівність записана зверху може бути представлена як

x^{n}={x^{n+1}}/{x},\quad n\geq 1.

Із визначення, що це рівняння є правдивим для всіх цілих чисел n і ненульових x, випливає що

{\begin{aligned}x^{0}&={x^{1}}/{x}=1\\x^{-1}&={x^{0}}/{x}={1}/{x}\end{aligned}}

і в більш загальній формі для будь-якого ненульового x і будь-яких невід'ємних цілих n,

x^{-n}={1}/{x^{n}}.

Видно, що це є вірним для всіх цілих чисел n.

Комбінаторна інтерпретація

Для невід'ємних цілих n і m, степінь n^m є числом функцій із множини з m елементів у множину з n елементів (див. кардинальне експонування). Така функція може бути представлена як m-кортежів із множини n-елементів (або слово із m-літер, що належить алфавіту, в якому є n-літер).

0⁵ = │ { } │ = 0	Не існує 5-елементного кортежу, який можна було б побудувати із пустої множини.
1⁴ = │ { (1,1,1,1) } │ = 1	Існує один 4-елементні кортежі із множини з одного елементу.
2³ = │ { (1,1,1), (1,1,2), (1,2,1), (1,2,2), (2,1,1), (2,1,2), (2,2,1), (2,2,2) } │ = 8	Існує вісім 3-елементні кортежі із множини з двох елементів.
3² = │ { (1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3) } │ = 9	Існує дев'ять 2-елементні кортежі із множини з трьох елементів.
4¹ = │ { (1), (2), (3), (4) } │ = 4	Існує чотири 1-елементні кортежі із множини з чотирьох елементів.
5⁰ = │ { () } │ = 1	Існує лише один 0-кортеж.

Тотожності і властивості

Наступні тотожності є вірними для всіх цілих показників, за умови що основа не є нулем:

{\begin{aligned}b^{m+n}&=b^{m}\cdot b^{n}\\(b^{m})^{n}&=b^{m\cdot n}\\(b\cdot c)^{n}&=b^{n}\cdot c^{n}\end{aligned}}

Операція піднесення до степеня не є комутативною. Як протилежність — операції додавання і множення комутативні. Наприклад, $2 + 3 = 3 + 2 = 5$ і $2 \cdot 3 = 3 \cdot 2 = 6$ , але $23 = 8$ , оскільки $32 = 9$ .

Операція піднесення до степеня також не є асоціативною. Приводячи приклад із додаванням і множенням, які є асоціативними, маємо: $(2 + 3) + 4 = 2 + (3 + 4) = 9$ і $(2 \cdot 3) \cdot 4 = 2 \cdot (3 \cdot 4) = 24$ , але 2³ на 4 дорівнює 8⁴ або 7003409600000000000♠4096, в той час як 2 на 3⁴ дорівнює 2⁸¹ або 7024241785163922925♠2417851639229258349412352. Без дужок, які задають порядок дій, загальноприйнятим є порядок зверху-вниз (або право-асоціативний), а не знизу-вгору[12] (or left-associative):

b^{p^{q}}=b^{(p^{q})}\neq (b^{p})^{q}=b^{(p\cdot q)}=b^{p\cdot q}.

В той час як Google і WolframAlpha в своїх додатках слідують вищезгаданому правилу, варто відмітити, що деякі комп'ютерні програми такі як Microsoft Excel або Matlab виконують операції зліва (зверху-вниз), тобто a^b^c розраховується як (a^b)^c.

Степені десятки

У десятковій системі числення, цілі степені числа 10 записуються у вигляді цифри 1 за якою слідує ряд нулів, що визначаються знаком і величиною показника. Наприклад, $7003100000000000000♠ 103 = 7003100000000000000♠ 1000$ і $6996100000000000000♠ 10 -4 = 6996100000000000000♠ 0.0001$ .

Степені із основою 10 використовується як експоненціальний запис в науці, для позначення дуже великих або малих чисел. Наприклад, 7008299792458000000♠299792458 м/с (швидкість світла у вакуумі, в метрах на секунду) може бути записана наступним чином: 7008299792458000000♠2.99792458×10⁸ м/с а потім апроксимовано до 7008299800000000000♠2.998×10⁸ м/с.

Префікси одиниць вимірювання теж основані на степенях числа 10 і використовуються для описання малих чи великих чисел. Наприклад, префікс кіло означає $7003100000000000000♠ 103 = 7003100000000000000♠ 1000$ , тому кілометр становить 7003100000000000000♠1000 метрів.

Степені двійки

Перші від'ємні степені двійки вживаються дуже часто, і мають особливі назви, такі як: половина і чверть.

Степені числа 2 з'являються у теорії множин, оскільки множина із n елементів має булеан, множина з усіх її підмножин, який має 2ⁿ елементів.

Цілі степені двійки важливі у комп'ютерній науці. Додатні цілі степені 2ⁿ задають максимальну можливу кількість значень для n-бітного цілого двійкового числа; наприклад, байт може приймати 2⁸ = 256 різних значень. Двійкова система числення дозволяє задавати будь-яке число як суму степенів 2, і записує їх як послідовність цифр 0 і 1, розділених двійковою точкою, де 1 означає ті степені двійки, які мають з'являтися в сумі; показник степеня визначається номером позиції цієї 1: невід'ємні показники впорядковані 1-ями зліва від точки (починаючи з 0), а від'ємні показники визначаються порядком в правій частині після коми.

Степені одиниці

Усі степені одиниці також дорівнюють одиниці: $1 n = 1$ .

Степені нуля

Якщо показник степеня є додатним числом, степінь нуля буде дорівнювати нулю: $0 n = 0$ , де $n > 0$ .

Якщо показник степеня є від'ємним, степінь нуля (0ⁿ, де $n < 0$ ) є невизначеною, оскільки було виконано ділення на нуль.

Якщо показник дорівнює нулю, в деяких випадках визначають це як $00 = 1$ , в той час як в інших варіантах залишають значення невизначеним.

Степені мінус одиниці

Якщо n є парним цілим, тоді $(-1) n = 1$ .

Якщо n є непарним цілим числом, тоді $(-1) n = -1$ .

Завдяки цій особливості, степені числа −1 зручно використовувати для вираження змінних послідовностей.

Великі степені

Границя числової послідовності степенів числа більшого за одиницю розходяться; іншими словами, послідовність зростає без обмеження:

b n \to \infty

при

n \to \infty

якщо

b > 1

Це читається як «b у степені n прямує до +∞ при n, що прямує до нескінченності коли b є більшою за одиницю».

Степені чисел із абсолютним значенням, що менше одиниці прямують до нуля:

b n \to 0

при

n \to \infty

якщо |b| < 1

Будь-який степінь одиниці, як уже зазначалося завжди дорівнює одиниці:

b n = 1

для всіх n якщо

b = 1

Степені числа –1 чергують значення 1 і –1 при тому n змінюється будучи то парним то непарним числом, і таким чином не прямує ні до якої границі при збільшенні n.

Якщо b < –1, $b n$ , чергується між все більшими додатними і від'ємними числами при тому як n чергується між парними і непарними значеннями, і таким чином не прямує до жодної границі при зростанні n.

Якщо значення числа, що підноситься до степеня змінюється при тому як прямує до 1 при показникові степеня що прямує до нескінченності, тоді існування границі і її значення не обов'язково підпадає у один випадків, що описано вище. Одним із важливих часткових випадків є

(1 + 1/ n) n \to e

при

n \to \infty

Степеневі функції

Степеневі функції для

n=1,3,5

Степеневі функції для

n=2,4,6

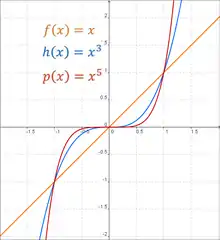
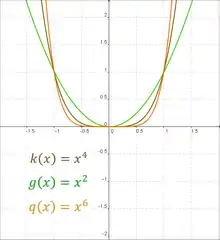
Функції дійсних значень вигляду $f(x)=cx^{n}$ із $c\neq 0$ називають степеневими функціями. Коли $n$ є цілим числом і $n\geq 1$ , існує дві основні різновидності: для парних і непарних $n$ . В загальному випадку для $c>0$ , якщо $n$ є парним числом із збільшенням $x$ $f(x)=cx^{n}$ буде прямувати до нескінченності із знаком плюс, а також у напрямку нескінченності із знаком плюс при зменшенні $x$ . Всі графіки із родини парних степеневих функцій мають загальну форму для $y=cx^{2}$ , маючи більш плоску форму в середині із збільшенням $n$ .[13] Функції із таким видом симетрії ( $f(-x)=f(x)$ ) називаються парними функціями.

Коли $n$ є парним, $f(x)$ має асимптотичну поведінку яка змінюється від додатних $x$ до від'ємних $x$ . Для $c>0$ , $f(x)=cx^{n}$ також прямуватиме до нескінченності із знаком плюс при збільшенні $x$ , але при зменшенні $x$ прямуватиме до нескінченності із знаком мінус. Усі графіки для сімейства парних степеневих функцій мають загальний вигляд для $y=cx^{3}$ , маючи більш плоску гладку форму в середині із збільшенням $n$ і втрачають усю гладкість перетворюючись в пряму лінію для $n=1$ . Функції із таким видом симетрії ( $f(-x)=-f(x)$ ) називаються непарними функціями.

Для $c<0$ , асимптотична поведінка із протилежними знаками зберігається у усіх випадках.[13]

Список степенів цілих чисел

n	n²	n³	n⁴	n⁵	n⁶	n⁷	n⁸	n⁹	n¹⁰
2	4	8	16	32	64	128	256	512	1,024
3	9	27	81	243	729	2,187	6,561	19,683	59,049
4	16	64	256	1,024	4,096	16,384	65,536	262,144	1,048,576
5	25	125	625	3,125	15,625	78,125	390,625	1,953,125	9,765,625
6	36	216	1,296	7,776	46,656	279,936	1,679,616	10,077,696	60,466,176
7	49	343	2,401	16,807	117,649	823,543	5,764,801	40,353,607	282,475,249
8	64	512	4,096	32,768	262,144	2,097,152	16,777,216	134,217,728	1,073,741,824
9	81	729	6,561	59,049	531,441	4,782,969	43,046,721	387,420,489	3,486,784,401
10	100	1,000	10,000	100,000	1,000,000	10,000,000	100,000,000	1,000,000,000	10,000,000,000

Раціональні показники

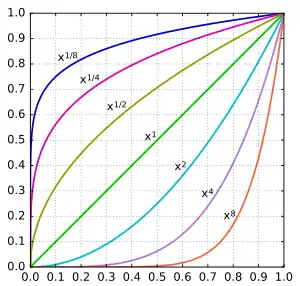
Зверху до низу вказані графіки функцій: x^1/8, x^1/4, x^1/2, x¹, x², x⁴, x⁸.

Коренем n-го степеня числа b є число x таке що $x n = b$ .

Якщо b є додатним дійсним числом і n є додатним цілим, тоді існує лише одне додатне дійсне значення, що є розв'язком рівняння $x n = b$ . Цей розв'язок називається головним коренем n-го степеня для b. Він позначається виразом ⁿ√b, де √ символ корінь; аналогічним чином, головний корінь можна записати як b^1/n. Наприклад: $4 1/2 = 2$ , $8 1/3 = 2$ .

Факт, що $x=b^{1/n}$ є розв'язком для $x^{n}=b$ , випливає із наступного запису:

x^{n}=\underbrace {b^{\frac {1}{n}}\times b^{\frac {1}{n}}\times \cdots \times b^{\frac {1}{n}}} _{n}=b^{\left({\frac {1}{n}}+{\frac {1}{n}}+\cdots +{\frac {1}{n}}\right)}=b^{\frac {n}{n}}=b^{1}=b.

Якщо n є парним, тоді $x n = b$ при умові, що b додатне число, має два дійсні розв'язки, якими є додатний і від'ємний корені n-го степеня, тобто, $b 1/ n > 0$ і $-(b 1/ n) < 0.$ Якщо b від'ємне, то рівняння не має розв'язку у вигляді дійсного числа при парних n.

Якщо n непарне, тоді $x n = b$ має лише один дійсний розв'язок. Розв'язок буде $b 1/ n$ додатним, якщо b є додатним, і від'ємним, якщо b від'ємне.

Піднесення додатного дійсного числа b до раціонального степеня u/v, де u є цілим і v є додатним цілим, і при розгляданні лише головних коренів, є наступним

b^{\frac {u}{v}}=\left(b^{u}\right)^{\frac {1}{v}}={\sqrt[{v}]{b^{u}}}=\left(b^{\frac {1}{v}}\right)^{u}=\left({\sqrt[{v}]{b}}\right)^{u}.

Піднесення від'ємного дійсного числа b до раціонального степеня u/v, де u/v є правильним дробом, дає результат, що є додатним дійсним числом, якщо u є парним, і таким чином v є непарним, оскільки тоді b^u є додатним; і дає від'ємний дійсний результат, якщо u і v обидва є непарними, оскільки тоді b^u є від'ємним. Випадок коли u є непарним, а v є парним, не можна визначити в рамках дійсних чисел, оскільки не існує такого дійсного числа x, щоб $x 2 k = -1$ ; при задаванні значення b^u/v в такому випадку необхідно використовувати уявну одиницю i.

Дійсні показники степеня

Тотожності і властивості що вказані вище для цілих степенів є вірними і для додатних дійсних чисел із не цілими показниками. Однак рівність

(b^{r})^{s}=b^{r\cdot s}

не може послідовно поширюватися на випадки коли b є від'ємним дійсним числом. Невірність цієї рівності є основою проблеми, що озвучується щодо степенів комплексних чисел.

Границі раціональних степенів

Дійсне число є границею послідовності раціональних наближень. Якщо

a=\lim _{n\rightarrow \infty }a_{n}

де $a_{n}$ — раціональні числа, то

x^{a}=\lim _{n\rightarrow \infty }x^{a_{n}}

.

Показникова функція

Одна із важливих математичних констант $e$ , що також називається числом Ейлера, приблизно дорівнює 2.718 і є основою натурального логарифму. Хоча піднесення у степінь числа e, по суті, можна трактувати так само як піднесення у степінь будь-якого іншого дійсного числа, такі степені, як виявилося, мають свої корисні і витончені властивості. Серед усього іншого, ці властивості дозволяють узагальнити степені e природним способом до інших типів степенів, таких як степені комплексних чисел або навіть матриць.

Як правило, нотація e^x зазвичай позначає узагальнене поняття експонування і називається показниковою функцією, exp(x), яку можна визначити багатьма способами, наприклад таким:

\exp(x)=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n}

Крім інших властивостей, exp задовольняє степеневе рівняння

\exp(x+y)=\exp(x)\cdot \exp(y).

Показникова функція є визначеною для всіх цілих, дрібних, дійсних, і комплексних значень змінної x. Експонента матриці добре визначена для квадратних матриць (у випадку яких експоненційне рівняння виконується лише коли матриці x і y є комутативними), і є корисною для вирішення систем лінійних диференційних рівнянь.

Дії зі степенями

При спрощенні виразів зі степенями можна використовувати декілька базових правил або законів, що називаються правилами дій зі степенями[14]:

1. При перемножуванні двох або більше різних степенів з однаковими основами показники степеня додаються

x^{a}\cdot x^{b}=x^{a+b}

2. При діленні одного степеня на інший з тією ж основою показник степеня знаменника віднімається від показника степеня чисельника.

{\frac {a^{m}}{a^{n}}}=a^{m-n}

3. При піднесені числа в якомусь степеню до іншого степеню показники перемножуються.

\left(x^{a}\right)^{b}=x^{a\cdot b}

4. При піднесенні будь-якого числа (окрім нуля) в степінь з показником 0 одержуємо 1, так $3^{0}=1$

5. При піднесенні числа до степеню з від'ємним цілим показником одержуємо величину, зворотну цьому числу з додатним степенем. Таким чином $3^{-4}={\frac {1}{3^{4}}}$ . Аналогічно ${\frac {1}{2^{-4}}}=2^{4}$

6. При піднесенні числа до дробового степеню, знаменник цього дробу є степінь кореня з числа, а чисельник є показником степеня числа. Так,

8^{\frac {2}{3}}={\sqrt[{3}]{8^{2}}}=(2)^{2}=4

Функції

В комбінаториці

В комбінаториці, кількість можливих розміщень з повтореннями із n елементів по m дорівнює n^m:[15]

{\hat {P}}(n,m)=n^{m}

Наприклад, із цифр 1, 2, 3, 4 можна скласти ${\hat {P}}(4,3)=4^{3}=64$ тризначних числа.

Посилання

Динамічні математичні моделі FIZMA.neT

Джерела

К. І. Швецов, Г. П. Бевз (1967). Довідник з елементарної математики. К. «Наукова думка»..
Бёрд Дж. Инженерная математика: Карманный справочник/ Пер. с. англ. — М.: Издательский дом «Додэка- XXI»,2008. — 544 с.
Судоплатов С. В., Овчинникова Е. В. (2002). Элементы дискретной математики. НГТУ. ISBN 5-7782-0332-2.

Примітки

К. І. Швецов, Г. П. Бевз (1967). Довідник з елементарної математики. К. «Наукова думка».
Джон Дж. О'Коннор та Едмунд Ф. Робертсон. Etymology of some common mathematical terms в архіві MacTutor (англ.)
For further analysis see The Sand Reckoner.
Джон Дж. О'Коннор та Едмунд Ф. Робертсон. Abu'l Hasan ibn Ali al Qalasadi в архіві MacTutor (англ.)
Cajori, Florian (2007). A History of Mathematical Notations; Vol I. Cosimo Classics. Pg 344 ISBN 1602066841
René Descartes, Discourse de la Méthode … (Leiden, (Netherlands): Jan Maire, 1637), appended book: La Géométrie, book one, page 299. From page 299: " … Et aa, ou a², pour multiplier a par soy mesme; Et a³, pour le multiplier encore une fois par a, & ainsi a l'infini ; … " (… and aa, or a², in order to multiply a by itself; and a³, in order to multiply it once more by a, and thus to infinity ; …)
See:
- Earliest Known Uses of Some of the Words of Mathematics
- Michael Stifel, Arithmetica integra (Nuremberg («Norimberga»), (Німеччина): Johannes Petreius, 1544), Liber III (Книга 3), Caput III (Глава 3): De Algorithmo numerorum Cossicorum. (Про алгоритми алгебри.), page 236. Штифель намагався отримати зручне представлення елементів геометричної прогресії. Заради цього він використав громіздку систему позначень. На 236-й сторінці він увів систему позначень для перших восьми елементів геометричної прогресії (з основою 1) і зробив запис: «Quemadmodum autem hic vides, quemlibet terminum progressionis cossicæ, suum habere exponentem in suo ordine (ut 1ze habet 1. 1ʓ habet 2 &c.) sic quilibet numerus cossicus, servat exponentem suæ denominationis implicite, qui ei serviat & utilis sit, potissimus in multiplicatione & divisione, ut paulo inferius dicam.» (Однак, Ви бачите, що кожен елемент послідовності має свій показник степеня (перший — 1, 1ʓ — 2, і т. д.), отже, кожне число неявно підпорядковане степеню залежному від його розташування, який [в свою чергу] підпорядковується йому і є корисним, здебільшого, при множенні та діленні, як я згадаю це трохи нижче.) [Зауваження: Більшість громіздких позначень Штифеля запозичені у Крістофа Рудольффа, який, у свою чергу, запозичив їх у книзі Леонардо Фібоначчі Liber Abaci (1202), де вони використовувались, як скорочення латинських слів res/radix (x), census/zensus (x²), and cubus (x³).]
Quinion, Michael. Zenzizenzizenzic - the eighth power of a number. World Wide Words. Процитовано 19 березня 2010.
Це визначення «інволюції» з'явилось у другому виданні OED, 1989, і в онлайн словнику Merriam-Webster . Останнє використання в цьому сенсі, наведене OED, починається з 1806 року.
Леонард Ейлер (1748) Введення в аналіз нескінченно малих, англ. видання, сторінка 75
Achatz, Thomas (2005). Technical Shop Mathematics (вид. 3rd). Industrial Press. с. 101. ISBN 0-8311-3086-5.
Raphael M. Robinson (1958). A report on primes of the form k · 2ⁿ + 1 and on factors of Fermat numbers (pdf). Proc. Amer. Math. Soc. 9: 677.
Anton, Howard; Bivens, Irl; Davis, Stephen. Calculus: Early Transcendentals (вид. 9th). John Wiley & Sons. с. 28.
Бёрд Дж. Инженерная математика: Карманный справочник — С. 27
Судоплатов С. В., Овчинникова Е. В. (2002). Элементы дискретной математики. НГТУ. ISBN 5-7782-0332-2.

Див. також

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] К. І. Швецов, Г. П. Бевз (1967). Довідник з елементарної математики. К. «Наукова думка».

[MacTutor-2] Джон Дж. О'Коннор та Едмунд Ф. Робертсон. Etymology of some common mathematical terms в архіві MacTutor (англ.)

[3] For further analysis see The Sand Reckoner.

[4] Джон Дж. О'Коннор та Едмунд Ф. Робертсон. Abu'l Hasan ibn Ali al Qalasadi в архіві MacTutor (англ.)

[5] Cajori, Florian (2007). A History of Mathematical Notations; Vol I. Cosimo Classics. Pg 344 ISBN 1602066841

[Descartes-6] René Descartes, Discourse de la Méthode … (Leiden, (Netherlands): Jan Maire, 1637), appended book: La Géométrie, book one, page 299. From page 299: " … Et aa, ou a², pour multiplier a par soy mesme; Et a³, pour le multiplier encore une fois par a, & ainsi a l'infini ; … " (… and aa, or a², in order to multiply a by itself; and a³, in order to multiply it once more by a, and thus to infinity ; …)

[7] See:
Earliest Known Uses of Some of the Words of Mathematics

Michael Stifel, Arithmetica integra (Nuremberg («Norimberga»), (Німеччина): Johannes Petreius, 1544), Liber III (Книга 3), Caput III (Глава 3): De Algorithmo numerorum Cossicorum. (Про алгоритми алгебри.), page 236. Штифель намагався отримати зручне представлення елементів геометричної прогресії. Заради цього він використав громіздку систему позначень. На 236-й сторінці він увів систему позначень для перших восьми елементів геометричної прогресії (з основою 1) і зробив запис: «Quemadmodum autem hic vides, quemlibet terminum progressionis cossicæ, suum habere exponentem in suo ordine (ut 1ze habet 1. 1ʓ habet 2 &c.) sic quilibet numerus cossicus, servat exponentem suæ denominationis implicite, qui ei serviat & utilis sit, potissimus in multiplicatione & divisione, ut paulo inferius dicam.» (Однак, Ви бачите, що кожен елемент послідовності має свій показник степеня (перший — 1, 1ʓ — 2, і т. д.), отже, кожне число неявно підпорядковане степеню залежному від його розташування, який [в свою чергу] підпорядковується йому і є корисним, здебільшого, при множенні та діленні, як я згадаю це трохи нижче.) [Зауваження: Більшість громіздких позначень Штифеля запозичені у Крістофа Рудольффа, який, у свою чергу, запозичив їх у книзі Леонардо Фібоначчі Liber Abaci (1202), де вони використовувались, як скорочення латинських слів res/radix (x), census/zensus (x²), and cubus (x³).]

[8] Earliest Known Uses of Some of the Words of Mathematics

[9] Michael Stifel, Arithmetica integra (Nuremberg («Norimberga»), (Німеччина): Johannes Petreius, 1544), Liber III (Книга 3), Caput III (Глава 3): De Algorithmo numerorum Cossicorum. (Про алгоритми алгебри.), page 236. Штифель намагався отримати зручне представлення елементів геометричної прогресії. Заради цього він використав громіздку систему позначень. На 236-й сторінці він увів систему позначень для перших восьми елементів геометричної прогресії (з основою 1) і зробив запис: «Quemadmodum autem hic vides, quemlibet terminum progressionis cossicæ, suum habere exponentem in suo ordine (ut 1ze habet 1. 1ʓ habet 2 &c.) sic quilibet numerus cossicus, servat exponentem suæ denominationis implicite, qui ei serviat & utilis sit, potissimus in multiplicatione & divisione, ut paulo inferius dicam.» (Однак, Ви бачите, що кожен елемент послідовності має свій показник степеня (перший — 1, 1ʓ — 2, і т. д.), отже, кожне число неявно підпорядковане степеню залежному від його розташування, який [в свою чергу] підпорядковується йому і є корисним, здебільшого, при множенні та діленні, як я згадаю це трохи нижче.) [Зауваження: Більшість громіздких позначень Штифеля запозичені у Крістофа Рудольффа, який, у свою чергу, запозичив їх у книзі Леонардо Фібоначчі Liber Abaci (1202), де вони використовувались, як скорочення латинських слів res/radix (x), census/zensus (x²), and cubus (x³).]

[8] Quinion, Michael. Zenzizenzizenzic - the eighth power of a number. World Wide Words. Процитовано 19 березня 2010.

[9] Це визначення «інволюції» з'явилось у другому виданні OED, 1989, і в онлайн словнику Merriam-Webster . Останнє використання в цьому сенсі, наведене OED, починається з 1806 року.

[10] Леонард Ейлер (1748) Введення в аналіз нескінченно малих, англ. видання, сторінка 75

[11] Achatz, Thomas (2005). Technical Shop Mathematics (вид. 3rd). Industrial Press. с. 101. ISBN 0-8311-3086-5.

[12] Raphael M. Robinson (1958). A report on primes of the form k · 2ⁿ + 1 and on factors of Fermat numbers (pdf). Proc. Amer. Math. Soc. 9: 677.

[:0-13] Anton, Howard; Bivens, Irl; Davis, Stephen. Calculus: Early Transcendentals (вид. 9th). John Wiley & Sons. с. 28.

[14] Бёрд Дж. Инженерная математика: Карманный справочник — С. 27

[15] Судоплатов С. В., Овчинникова Е. В. (2002). Элементы дискретной математики. НГТУ. ISBN 5-7782-0332-2.