Гіпотеза Тета (теорія графів)

Гіпотеза Тета — спростована математична гіпотеза про те, що будь-який 3-зв'язний планарний кубічний граф має гамільтонів цикл, що проходить через усі його вершини .

Висловлена в 1884 році Пітером Тетом [1], спростована в 1946 році Вільямом Таттом [2], який побудував контрприклад з 25 гранями, 69 ребрами і 46 вершинами — граф Татта. Пізніше, 1988 року, знайдено контрприклад з 21 гранню, 57 ребрами і 38 вершинами і доведено, що цей граф мінімальний[3].

Умова 3-регулярності (3-регулярні графи називаються кубічними) необхідна, оскільки існують багатогранники, такі як ромбододекаедр. Ромбододекаедр утворює двочастковий граф і будь-який гамільтонів цикл у цьому графі має почергово змінювати частки (сторони) графа, так що число вершин в частках має бути однаковим, проте граф має шість вершин степеня 4 на одному боці і вісім вершин степеня 3 на іншому.

Якби гіпотеза була правильна, то з неї випливав би простий розв'язок задачі чотирьох фарб. Згідно з Тетом, задача чотирьох фарб еквівалентна задачі пошуку реберної 3-розмальовки кубічних планарних графів без мостів. У гамільтоновому кубічному планарному графі таку розмальовку ребер легко знайти — по черзі використовуємо два кольори для розмальовування ребер уздовж гамільтонового циклу, а третім кольором пофарбуємо решту ребер. Альтернативно можна побудувати розмальовку в чотири кольори граней гамільтонового кубічного планарного графа прямо, якщо використовувати два кольори для розмальовування граней всередині циклу і два кольори для граней зовні.

Контрприклад Татта
Фрагмент Татта

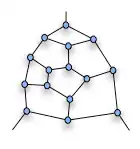
Ключем контрприкладу є граф, який зараз називають фрагментом Татта. Якщо цей фрагмент є частиною більшого графа, будь-який гамільтонів цикл має проходити через (висяче) ребро при верхній вершині (і через одне з нижніх ребер). Шлях не може увійти через нижнє ребро і вийти через інше нижнє ребро.

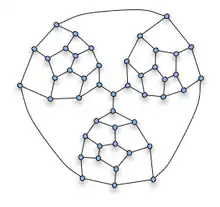
Контрприклад Татта — три фрагмента Татта, з'єднані в центрі

Фрагмент Татта використовується для побудови негамільтонового графа Татта, якщо скласти докупи три таких фрагмента. «Обов'язкові» ребра фрагментів, які повинні бути частинами гамільтонового шляху через фрагмент, з'єднані в центрі. Оскільки будь-який цикл може проходити тільки через два з трьох ребер у центрі, гамільтонового циклу для цього графа бути не може. Одержаний граф Татта є 3-зв'язним і планарним, так що він є графом багатогранника за теоремою Штайніца. Граф має 25 граней, 69 ребер і 46 вершин. Геометрично граф можна отримати з тетраедра (грані якого відповідають чотирьом великим граням на малюнку — три грані між парами фрагментів, а четверта грань є зовнішньою) шляхом багаторазового усічення трьох його вершин.

Менші контрприклади

Як показали Голтон і Маккей 1988 року[3], існує рівно шість негамільтонових 3-регулярних багатогранників з 38 вершинами. Багатогранники утворені заміною двох вершин п'ятикутної призми тим самим фрагментом з прикладу Татта.

Див. також
  • Теорема Грінберга — необхідна умова існування гамільтонового циклу, яку можна використати, щоб показати, що граф є контрприкладом до гіпотези Тета.
  • Гіпотеза Барнета — залишається відкритим удосконаленням гіпотези Тета; гіпотеза стверджує, що будь-який двочастковий кубічний багатогранний граф є гамільтоновим.[4]

Примітки
  1. Tait, 1884.
  2. Tutte, 1946.
  3. Holton, McKay, 1988.
  4. Barnette's conjecture, the Open Problem Garden, retrieved 2009-10-12.

Література
  • D. A. Holton, B. D. McKay. The smallest non-Hamiltonian 3-connected cubic planar graphs have 38 vertices // Journal of Combinatorial Theory, Series B. — 1988. — Т. 45, вип. 3. — С. 305–319. — DOI:10.1016/0095-8956(88)90075-5.
  • P. G. Tait. Listing's Topologie // Philosophical Magazine (5th ser.). — 1884. — Т. 17. — С. 30–46. Статья перепечатана в Scientific Papers, том II, стр. 85-98.
  • W. T. Tutte. On Hamiltonian circuits // Journal of the London Mathematical Society. — 1946. — Т. 21, вип. 2. — С. 98–101. — DOI:10.1112/jlms/s1-21.2.98.

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.