Деревна глибина (теорія графів)

Деревну глибину графу G можна визначити як мінімальну висоту лісу F із властивістю, що будь-яке ребро графу G з'єднує пару вершин, пов'язаних відношенням предок-нащадок у F[4]. Якщо G зв'язний, цей ліс має бути єдиним деревом. Ліс не обов'язково має бути підграфом графу G, але якщо є, то це дерево Тремо для G.

Множина пар предок-нащадок у F утворює тривіально досконалий граф, і висота F є розміром найбільшої кліки цього графу. Таким чином, деревну глибину альтернативно можна визначити як розмір найбільшої кліки в тривіально досконалому суперграфі графу G, що є дзеркальним відбиттям деревної ширини, яка на одиницю менша від розміру найбільшої кліки в хордальному суперграфі графу G[5].

Інше визначення таке:

• ${\displaystyle 1}$ якщо |G|=1
• ${\displaystyle 1+\min _{v\in V}td(G-v)}$, якщо G зв'язний і |G|>1
• ${\displaystyle \max _{i}td(G_{i})}$ в іншому випадку, де V — множина вершин графу G і ${\displaystyle G_{i}}$ — зв'язні компоненти G[6]. Це визначення віддзеркалює визначення циклічного рангу орієнтованих графів, яке використовує строгу зв'язність і строго пов'язані компоненти замість неорієнтованої зв'язності і зв'язних компонент.

Деревну глибину можна визначити з використанням розфарбовування графів. Центроване розфарбування графу — це розфарбування вершин, яка має властивість, що в будь-якому зв'язному породженому підграфі є колір, який зустрічається рівно один раз. Тоді деревна глибина — це найменше число кольорів, необхідних для центрованого розфарбовування графу. Якщо F — ліс з висотою d, який має властивість, що кожне ребро графу G з'єднує предка і нащадка в дереві, то можна отримати центроване розфарбування графу G d кольорами розфарбувавши кожну вершину в колір з номером, рівним відстані від кореня у графі F[7].

Нарешті, можна визначити його в термінах фішкової гри. А саме, точно як гру переслідування-ухилення. Уявімо таку гру на неорієнтованому графі. Є два гравці, грабіжник і поліцейський. Грабіжник має одну фішку, яку він рухає вздовж ребер графу. Поліцейський має необмежену кількість фішок, але він хоче мінімізувати кількість використаних фішок. Поліцейський не може пересувати своїх фішок, поміщених на граф. Гра відбувається так. Грабіжник розміщує свою фішку, потім поліцейський повідомляє, куди він хоче поставити наступну фішку і грабіжник після цього може пересунути свою фішку вздовж ребер, але не через зайняті вершини. Гра завершується, коли поліцейський поміщає наступну фішку поверх фішки грабіжника. Деревна глибина даного графу визначає найменше число фішок, необхідних для гарантованого виграшу[8][9]. Для зірки достатньо двох фішок — розміщуємо першу фішку в центрі зірки, змушуючи грабіжника перейти в якийсь промінь, а потім поміщаємо другу фішку на фішку грабіжника. Для шляху з ${\displaystyle n}$ вершинами поліцейський використовує стратегію двійкового пошуку, яка гарантує використання не більше ${\displaystyle \lceil \log _{2}(n+1)\rceil }$ фішок.

Деревна глибина повного графу K₄ і повного двочастинного графу K_3,3 дорівнює чотирьом, тоді як деревна глибина шляху P₇ дорівнює трьом.

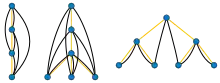
Деревна глибина повного графу дорівнює кількості його вершин, і в цьому випадку єдиним можливим лісом F, для якого будь-яка пара вершин перебуває у відношенні предок-нащадок, є одиничний шлях. Схожим чином деревна глибина повного двочастинного графу K_x,y дорівнює min(x,y) + 1, і як би ми не розташовували вершини, листки лісу F повинні мати принаймні min(x,y) предків F. Ліс, на якому досягається min(x,y) + 1, можна побудувати, утворивши шлях з вершин меншої за розміром частки графу, а вершини більшої частки формують листки дерева F, сполучені з нижньою вершиною шляху.

Деревна глибина шляху з n вершинами дорівнює рівно ${\displaystyle \lceil \log _{2}(n+1)\rceil }$. Ліс F, що подає цей шлях з такою глибиною, можна утворити, помістивши корінь у середню точку шляху F і продовжуючи рекурсію в двох менших шляхах з обох боків від кореня[10].

Будь-який ліс із n вершинами має деревну глибину O(log n). Для лісу можна завжди знайти стале число вершин, видалення яких дає ліс, який можна розділити на два менших підліси з максимум 2n/3 вершин у кожному. Рекурсивно ділячи ці два підліси, легко можна досягти логарифмічної верхньої межі деревної глибини. Та ж техніка, застосована до деревної декомпозиції графу, показує, що, якщо деревна ширина n-вершинного графу G дорівнює t, тоді деревна глибина графу G дорівнює O(t log n).[11][12] Оскільки зовніпланарні графи, паралельно-послідовні графи і графи Халіна мають обмежену деревну ширину, вони всі теж мають максимум логарифмічну деревну глибину.

З іншого боку, деревна ширина графу не перевершує його деревної глибини. Точніше, деревна ширина не перевершує шляхової ширини графу, яка максимум на одиницю менша від його деревної глибини[11][13].

Мінор графу G — це інший граф, утворений з підграфу графу G стягуванням деяких ребер. Деревна глибина монотонна за мінорами — будь-який мінор графу G має деревну глибину, що не перевищує деревної глибини самого графу G[14]. Таким чином, за теоремою Робертсона — Сеймура, для будь-якого фіксованого d множина графів із деревною глибиною, що не перевершує d, має скінченне число заборонених мінорів.

Якщо C — клас графів, замкнутих відносно утворення мінорів, то графи C мають деревну глибину ${\displaystyle O(1)}$ тоді й лише тоді, коли C не включає всіх шляхів[15].

Деревна глибина має тісний зв'язок з теорією породжених підграфів графу. В класі графів, що мають деревну глибину не більше d (для будь-якого фіксованого натурального d), властивість бути породженим підграфом є цілком квазівпорядкованою[16]. Основна ідея доведення, що цей зв'язок цілком квазівпорядкований, полягає у використанні індукції за d. Ліси висоти d можна інтерпретувати як послідовність лісів висоти d − 1 (утворених видаленням коренів дерев висоти d) і можна використовувати лему Гігмана, щоб показати, що ці послідовності цілком квазівпорядковані.

Із цілком квазівпорядкованості випливає, що будь-яка властивість графу, монотонна за породженими підграфами, має скінченне число заборонених породжених підграфів, а тому може бути перевірена за поліноміальний час на графах з обмеженою деревною глибиною. Графи з деревною глибиною, що не перевершує d, самі по собі мають скінченне число заборонених породжених підграфів. Нешетрил і Оссона де Мендез[17] показали 14 заборонених підграфів для графів з деревною шириною три і менше (з посиланням на тези дисертації 2007 року Зденека Дворака).

Якщо C є класом графів з обмеженою виродженістю, графи у множині C мають обмежену деревну ширину тоді і тільки тоді, коли існує шлях, який не може з'явитися як породжений підграф у C[15].

Визначення глибини дерева є складною обчислювальною задачею — відповідна задача розпізнавання NP-повна[18]. Завдання залишається NP-повною для двочасткових графів[1], як і для хордальних графів[19].

З позитивних моментів — деревну глибину можна обчислити за поліноміальний час для інтервальних графів[20], як і для графів перестановок, трапецеїдальних графів, графів перетинів дуг кіл, циклічних графів перестановок і графів копорівнянності обмежених розмірностей[21]. Для неорієнтованих дерев деревну глибину можна обчислити за лінійний час[22][23].

Бодлендер, Гілберт, Хафстейнссон і Клокс[11] запропонували апроксимаційний алгоритм пошуку деревної глибини з апроксимаційним коефіцієнтом ${\displaystyle O((\log n)^{2})}$. Алгоритм заснований на факті, що деревна глибина логарифмічно залежить від деревної ширини графу.

Оскільки деревна глибина монотонна за мінорами графу, задача її пошуку фіксовано-параметрично розв'язна — існує алгоритм обчислення деревної глибини, що працює за час ${\displaystyle f(d)n^{O(1)}}$, де d — глибина даного графу і n — число вершин. Таким чином, для будь-якого фіксованого значення d задача перевірки, чи не перевершує деревна глибина значення d, може бути розв'язана за поліноміальний час. Конкретніше — залежність від n у цьому алгоритмі можна зробити лінійною таким чином: будуємо дерево пошуку в глибину і перевіряємо, перевищує глибина дерева величину 2^d чи ні. Якщо перевищує, то глибина дерева більша від d і задачу роз'язано. Якщо ні, можна скористатись побудовою дерева пошуку на невелику глибину для декомпозиції дерева і стандартною технікою динамічного програмування для графів з обмеженою деревною шириною, щоб обчислити глибину за лінійний час[24]. Більш складний алгоритм розв'язування за лінійний час, заснований на планарності мінорів, що виключаються під час пошуку в глибину, запропонували раніше Бодлендер, Деоган, Дженсен та Клокс[1]. Покращений параметричний алгоритм див. у Райдля, Россманіта, Вілламіла і Сікдара[25].

Можна обчислити глибину дерева точно для графів, значення глибини для яких може бути великим, за час O(cⁿ) з константою c, трохи меншою від 2.[26]

• Bengt Aspvall, Pinar Heggernes. Finding Minimum Height Elimination Trees for Interval Graphs in Polynomial Time // BIT. — 1994. — Т. 34, вип. 4 (21 січня). — С. 484–509. — DOI:10.1007/BF01934264..
• Hans L. Bodlaender, Jitender S. Deogun, Klaus Jansen, Ton Kloks, Dieter Kratsch, Haiko Müller, Zsolt Tuza. Rankings of graphs // SIAM Journal on Discrete Mathematics. — 1998. — Т. 11, вип. 1 (21 січня). — С. 168–181. — DOI:10.1137/S0895480195282550.^{[недоступне посилання з Июнь 2018]}.
• Hans L. Bodlaender, John R. Gilbert, Hjálmtýr Hafsteinsson, Ton Kloks. Approximating treewidth, pathwidth, frontsize, and shortest elimination tree // Journal of Algorithms. — 1995. — Т. 18, вип. 2 (21 січня). — С. 238–255. — DOI:10.1006/jagm.1995.1009. — CiteSeerX: 10.1.1.29.7198..
• Jitender S. Deogun, Ton Kloks, Dieter Kratsch, Haiko Müller. On the vertex ranking problem for trapezoid, circular-arc and other graphs // Discrete Applied Mathematics. — 1999. — Т. 98 (21 січня). — С. 39–34. — DOI:10.1016/S0166-218X(99)00179-1..
• D. Dereniowski, A. Nadolski. Vertex rankings of chordal graphs and weighted trees // Information Processing Letters. — 2006. — Т. 98 (21 січня). — С. 96–100. — DOI:10.1016/j.ipl.2005.12.006..
• Fedor V. Fomin, Archontia C. Giannopoulou, Michał Pilipczuk. Parameterized and Exact Computation: 8th International Symposium, IPEC 2013, Sophia Antipolis, France, September 4-6, 2013, Revised Selected Papers / Gregory Gutin, Stefan Szeider. — 2013. — Т. 8246. — С. 137–149. — (Lecture Notes in Computer Science) — DOI:10.1007/978-3-319-03898-8_13..
• Hermann Gruber, Markus Holzer. Proc. 35th International Colloquium on Automata, Languages and Programming. — Springer-Verlag, 2008. — Т. 5126. — С. 39–50. — (Lecture Notes on Computer Science) — DOI:10.1007/978-3-540-70583-3_4..
• Paul Hunter. 18th International Symposium on Fundamentals of Computation Theory. — Springer-Verlag, 2011. — Т. 6914. — С. 217–228. — (Lecture Notes on Computer Science) — DOI:10.1007/978-3-642-22953-4_19.
• Ananth V. Iyer, H. Donald Ratliff, Gopalakrishnan Vijayan. Optimal node ranking of trees // Information Processing Letters. — 1988. — Т. 28 (21 січня). — С. 225–201. — DOI:10.1016/0020-0190(88)90194-9..
• Jaroslav Nešetřil, Patrice Ossona de Mendez. Sparsity: Graphs, Structures, and Algorithms. — Heidelberg : Springer, 2012. — Т. 28. — С. 115–144. — (Algorithms and Combinatorics) — ISBN 978-3-642-27874-7. — DOI:10.1007/978-3-642-27875-4..
• Alex Pothen. The complexity of optimal elimination trees. — Pennsylvania State University, 1988. — (Tech. Report CS-88-13).
• Felix Reidl, Peter Rossmanith, Fernando Sánchez Villaamil, Somnath Sikdar. Automata, Languages, and Programming: 41st International Colloquium, ICALP 2014, Copenhagen, Denmark, July 8–11, 2014, Proceedings, Part I / Javier Esparza, Pierre Fraigniaud, Thore Husfeldt, Elias Koutsoupias. — 2014. — Т. 8572. — С. 931–942. — (Lecture Notes in Computer Science) — DOI:10.1007/978-3-662-43948-7_77..
• Benjamin Rossman. Homomorphism preservation theorems // Journal of the ACM. — 2008. — Т. 55, вип. 3 (21 січня). — С. Article 15. — DOI:10.1145/1379759.1379763..
• Alejandro A. Schäffer. Optimal node ranking of trees in linear time // Information Processing Letters. — 1989. — Т. 33 (21 січня). — С. 91–19. — DOI:10.1016/0020-0190(89)90161-0..