Шляхова ширина графу
У теорії графів шляхова декомпозиція графу G — це, неформально, подання графу G у вигляді «потовщеного» шляху[1], а шляхова ширина графу G — це число, що вимірює, наскільки граф G був потовщений. Формальніше, шляхова декомпозиція — це послідовності вершин підмножини графу G, такі, що кінцеві вершини кожного ребра з'являються в одній з підмножин і кожна вершина належить (хоча б) одній множині[2], а шляхова ширина на одиницю менша від розміру найбільшої множини в цій декомпозиції. Шляхова ширина відома також як інтервальна товщина (на одиницю менше від розміру найбільшої кліки інтервального суперграфу графу G), величина вершинного розділення, чи вершинно-пошукове число[3][4].
Шляхова ширина і шляхова декомпозиція є тісною аналогією з деревною шириною і деревною декомпозицією. Вони відіграють ключову роль у теорії мінорів графу — сімейства графів, які замкнуті відносно мінорів графу і не включають усі дерева, можна схарактеризувати як такі, що мають обмежену шляхову ширину[2], і «вихори», що виникають у загальній структурній теорії сімейств графів, замкнутих за мінором, мають обмежену шляхову ширину[5]. Шляхова ширина і графи з обмеженою шляховою шириною застосовуються в розробці НВІС, візуалізації графів та комп'ютерній лінгвістиці.
Задача знаходження шляхової ширини довільних графів є NP-складною. Більше того, NP-складною є навіть задача апроксимації шляхової ширини точно[6][7]. Однак ця задача є фіксовано-параметрично розв'язною — перевірку, чи має граф шляхову ширину k, можна здійснити за час, який лінійно залежить від розміру графу, але суперекспоненціально від k. Крім того, для деяких особливих класів графів, таких як дерева, шляхову ширину можна обчислити за поліноміальний час, не залежний від k[8][9]. Багато задач теорії графів можна ефективно розв'язати на графах з обмеженою шляховою шириною за допомогою динамічного програмування на шляховій декомпозиції графу[10]. Деревну декомпозицію можна також використовувати для оцінювання ємнісної складності алгоритмів динамічного програмування на графах з обмеженою деревною шириною[11].
Визначення

У першій відомій серії статей про мінори графу Робертсон і Сеймур[2] визначили шляхову декомпозицію графу G як послідовність підмножин Xi вершин графу G з двома властивостями:
- Для кожного ребра G існує i, таке, що обидві кінцеві точки ребра належать підмножині Xi.
- Для будь-яких трьох індексів i ≤ j ≤ k, Xi ∩ Xk ⊆ Xj.
Друга з цих двох властивостей еквівалентна вимозі, що підмножини, які містять будь-яку вершину, утворюють неперервну підпослідовність усієї послідовності. Мовою пізнішої серії робіт Робертсона і Сеймура про мінори графу, шляхова декомпозиція — це деревна декомпозиція (X,T), в якій дерево T декомпозиції, що лежить нижче, є шляхом.
Ширина шляхової декомпозиції визначається так само, як і для деревної декомпозиції, як maxi |Xi| − 1, а шляхова ширина графу G дорівнює мінімальній ширині всіх шляхових декомпозицій графу G. Віднімання одиниці від розміру Xi в цьому визначенні мало впливає на більшість застосувань шляхової ширини, але зате робить шляхову ширину шляху рівною одиниці.
Альтернативні описи
Як пише Бодлендер[3] шляхову ширину можна описати багатьма еквівалентними способами.
Склеювання послідовностей
Деревну декомпозицію можна описати як послідовність графів Gi, які склеєні шляхом ототожнення пар вершин у сусідніх графах послідовності, і результатом цього склеювання є граф G. Як графи Gi можна взяти породжені підграфи множин Xi у першому визначенні шляхової декомпозиції, зі склеюванням вершин у сусідніх породжених підграфах, якщо ці вершини породжені тією ж самою вершиною з G. З іншого боку можна відновити Xi як множини вершин графів Gi. Ширина деревної декомпозиції тоді на одиницю менша від максимального числа вершин в одному з графів Gi[2].
Інтервальна товщина
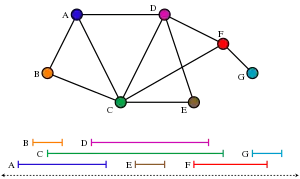
Шляхова ширина будь-якого графу G на одиницю менша від найменшого клікового числа інтервального графу, що містить G як підграф[13]. Тобто для будь-якої деревної декомпозиції графу G можна знайти інтервальний суперграф, і для будь-якого інтервального суперграфу G можна знайти деревну декомпозицію графу G, ширина декомпозиції якої на одиницю менша від клікового числа інтервального графу.
З одного боку, припустимо, що деревна декомпозиція графу G задана. Тоді можна уявити вершини декомпозиції як точки на прямій (в тому порядку, в якому вони входять до шляху) і подати кожну вершину v як замкнутий інтервал, для якого ці точки є кінцевими. Наприклад, нехай (X1, …, Xr) — шляхова декомпозиція графу G, точки на прямій — [1, …, r], тоді подання вершини v — це інтервал . Тоді деревна декомпозиція вершин, що містять v, відповідає кінцевим точкам інтервалу для v. Граф перетинів інтервалів, утворений з вершин G, — це інтервальний граф, що містить G як підграф. Його максимальні кліки задаються множиною інтервалів, що містять точки представлення, і їх розмір найбільшої кліки на одиницю більший від шляхової ширини графу G.
З іншого боку, якщо G — підграф інтервального графу з кліковим числом p+1, то граф G має деревну декомпозицію ширини p, вершини якої задані максимальними кліками інтервального графу. Наприклад, інтервальний граф, показаний з його інтервальним поданням на рисунку, має деревну декомпозицію з п'ятьма вершинами, відповідними п'ятьом максимальним клікам ABC, ACD, CDE, CDF та FG. Розмір максимальної кліки дорівнює трьом, а ширина цієї деревної декомпозиції дорівнює двом.
Ця еквівалентність між шляховою шириною й інтервальною товщиною є тісною аналогією з еквівалентністю між деревною шириною і мінімальним кліковим числом (мінус одиниця) хордального графу, для якого даний граф є підграфом. Інтервальні графи є особливим випадком хордальних графів, а хордальні графи можна подати у вигляді графів перетинів піддерев спільних дерев, що узагальнює підхід, за якого інтервальні графи інтерпретуються як графи перетинів підшляхів шляху.
Величина вершинного поділу
Припустимо, що вершини графу G лінійно впорядковані. Тоді величина вершинного поділу графу G — це найменше число s, таке, що для кожної вершини v максимум s вершин передують v в упорядкуванні, які мають v або одну з наступних за нею вершин в околі. Величина вершинного поділу графу G — це мінімальна величина вершинного поділу будь-якого лінійного впорядкування графу G. Величину вершинного поділу ввели Елліс, Садбороу та Тернер[14], і вона дорівнює шляховій ширині графу G[15][16]. Це випливає з раніше згаданої еквівалентності інтервальних графів і клікових чисел — якщо G є підграфом інтервального графу I, поданого (як на рисунку) так, що всі кінці інтервалів різні, то порядок лівих кінців інтервалів графу I мають величину вершинного поділу на одиницю меншу за клікове число графу I. З іншого боку, з лінійного впорядкування графу G можна отримати інтервальне подання, в якому ліва кінцева точка інтервалу для вершини v є позицією в упорядкуванні, а права кінцева точка є позицією сусіда v, який в упорядкуванні останній.
Вершинно-пошукове число
Гра «пошук вершини» на графі — це вид гри переслідування-ухилення, в якій множина переслідувачів спільно намагаються вистежити втікача, який сховався в графі. Переслідувачі розміщуються у вершинах графу, тоді як утікач може перебувати на будь-якому ребрі графу, його місце розташування і ходи переслідувачам не помітні. Під час чергового ходу деякі (або всі) переслідувачі можуть перейти (довільним чином, не обов'язково уздовж ребер) з однієї вершини в іншу, а втікач рухається потім уздовж будь-якого шляху на графі, але не може проходити через зайняті переслідувачами вершини. Втікач спійманий, коли обидва кінці дуги, на якій він перебуває, зайняті переслідувачами. Вершинно-пошукове число графу — це найменше число переслідувачів, необхідних для гарантованого впіймання втікача незалежно від його поведінки. Як показали Кіроузіс і Пападімітріу[17], вершинно-пошукове число графу дорівнює його інтервальній товщині. Оптимальною стратегією для переслідувачів є ходи, в яких переслідувачі послідовно утворюють розділювальні множини лінійного впорядкування з мінімальною величиною вершинного поділу.
Межі

Будь-який граф з n вершинами і шляховою шириною k має максимум k(n − k + (k − 1)/2)) ребер, і максимальні графи з шляховою шириною k (графи, до яких не можна додати ребро без збільшення шляхової ширини) мають точно таке число ребер. Максимальний граф з шляховою шириною k повинен бути або k-шляхом, або k-гусеницею, тобто одного з двох особливих видів k-дерева. k-дерево — це хордальный граф з точно n − k максимальними кліками, кожна з яких містить k + 1 вершину. В k-дереві, яке саме не є (k + 1)-клікою, кожна максимальна кліка або ділить граф на дві або більше компоненти, або містить одиничну листову вершину, вершину, яка належить тільки одній максимальній кліці. k-шлях — це k-дерево з максимум двома листками, а k-гусениця — це k-дерево, яке можна поділити на k-шлях і множину k-листків, кожен з яких суміжний з сепаратором k-кліки k-шляху. Зокрема, максимальні графи шляхової ширини одиниця — це точно графи-гусениці[18].
Оскільки шляхові декомпозиції є особливими випадками деревних декомпозицій, шляхова ширина будь-якого графу більша або дорівнює його деревній ширині. Шляхова ширина також менша або дорівнює ширині розрізу, мінімального числа ребер, які перетинають будь-який перетин між вершинами з меншим індексом і великим індексом в оптимальному лінійному впорядкуванні вершин графу. Це випливає з факту, що величина вершинного поділу, число вершин з меншим індексом з сусідами, що мають більший індекс, не більша від числа розрізаючих ребер[19][20]. З цієї ж причини ширина розрізу не перевищує шляхової ширини, помноженої на максимальний степінь вершин у даному графі[21][22].
Будь-який ліс з n вершинами має шляхову ширину O(log n)[23][24][25]. Для лісу можна завжди знайти стале число вершин, видалення яких приводить до лісу, який можна розбити на два менших ліси з максимум 2n/3 вершин у кожному з цих лісів. Лінійне впорядкування, утворене рекурсивним застосуванням такого розбиття, має логарифмічне пошукове число для вершин. Та сама техніка, застосована до деревної декомпозиції графу, показує, що якщо деревна ширина графу G з n вершинами дорівнює t, то шляхова ширина графу G дорівнює O(t log n)[26][27]. Оскільки зовніпланарні графи, паралельно-послідовні графи та графи Халіна всі мають обмежену деревну ширину, всі вони мають максимум логарифмічну шляхову ширину.
Крім того, що шляхова ширина пов'язана з деревною шириною, вона пов'язана з кліковою шириною і шириною розрізу через реберні графи. Реберний граф L(G) графу G має вершину для кожного ребра графу G і дві вершини в L(G) суміжні, якщо відповідні два ребра G мають спільні кінцеві точки. Будь-яке сімейство графів має обмежену шляхову ширину тоді й лише тоді, коли його реберні графи мають обмежену лінійну клікову ширину, де лінійна клікова ширина замінює операцію об'єднання у визначенні клікової ширини на операцію приєднання окремої нової вершини[28]. Якщо зв'язний граф з трьома або більше вершинами має максимальний степінь 3, його ширина розрізу дорівнює величині вершинного поділу його реберного графу[29].
В будь-якому планарному графі шляхова ширина в гіршому випадку пропорційна квадратному кореню від кількості вершин[30]. Один зі способів пошуку шляхової декомпозиції з такою шириною — (подібно до шляхової декомпозиції з логарифмічною деревною шириною, описаної вище) використовувати теорему про планарне розбиття, щоб знайти множини з O(√n) вершин, видалення яких розбиває граф на два підграфи з максимум 2n/3 вершинами в кожному, і з'єднати рекурсивно побудовані для цих двох підграфів шляхові декомпозиції. Цю ж техніку можна застосувати до будь-якого класу графів, для яких виконується подібна теорема про розбиття[31]. Оскільки будь-яке сімейство графів, замкнуте щодо взяття мінорів, як і в разі планарних графів, має розбивальну множину вершин розміру O(√n)[32], звідси випливає, що шляхова ширина графів у будь-якому фіксованому замкнутому відносно мінорів сімействі знову дорівнює O(√n). Для деяких класів планарних графів шляхова ширина графу і шляхова ширина його двоїстого графу повинні лежати в інтервалі, межі якого лінійно залежать від значень — такі межі відомі для двозв'язних зовнішніх планарних графів[33][34] і для графів багатогранників[35][36]. Для двозв'язних планарних графів шляхова ширина двоїстого графу менша, ніж шляхова ширина реберного графу[37]. Залишається відкритим питання, чи буде шляхова ширина планарного графу і його двоїстого завжди в лінійних межах для інших випадків.
Для деяких класів графів доведено, що шляхова ширина графу і деревна ширина завжди рівні між собою — це виконується для кографів[38], графів перестановки[39], доповнень графів порівнянності і графів порівнянності[40] інтервальних порядків[41].
Шаблон:Unsolved В будь-якому кубічному графі або, більш загально, будь-якому графі з максимальним степенем вершин 3, шляхова ширина не перевищує n/6 + o(n), де n — кількість вершин графу. Існують кубічні графи зі шляховою шириною 0,082n, але невідомо, як скоротити цей розрив між нижньою межею і верхньою межею n/6[42].
Обчислення шляхових декомпозицій
Визначення, чи не перевищує шляхова ширина заданого значення k для заданого графу, є NP-повною задачею, якщо k є вхідним параметром[6]. Найвідоміші часові межі обчислення шляхової ширини довільного графу з n вершинами мають вигляд O(2n nc) за деякої константи c[43]. Проте відомі деякі алгоритми обчислення шляхової декомпозиції з більшою ефективністю, якщо шляхова ширина мала, якщо клас вхідних графів обмежений, або потрібно обчислити шляхову ширину приблизно.
Фіксовано-параметрично розв'язність
Шляхова ширина фіксовано-параметрично розв'язна — для будь-якого сталого k можна перевірити, чи не перевершує шляхова ширина величини k, і, якщо не перевершує, знайти шляхову декомпозицію ширини k за лінійний час. У цілому, ці алгоритми працюють у два етапи. На першому етапі використовується припущення, що граф має шляхову ширину k, для пошуку шляхової декомпозиції або деревної декомпозиції. Ця декомпозиція не оптимальна, але її ширина може бути обмежена функцією від k. На другому етапі застосовується алгоритм динамічного програмування для пошуку оптимальної декомпозиції. Однак часові межі для відомих алгоритмів цього типу експоненціальні від k2 і не становлять практичного інтересу, хіба що для малих значень k[44]. Для випадку k = 2 Фляйтер дав алгоритм з лінійним часом роботи, заснований на структурній декомпозиції графів зі шляховою шириною 2[45].
Особливі класи графів
Бодлендер [8] дав огляд складності задач обчислення шляхової ширини на різних особливих класах графів. Визначення, чи перевищує шляхова ширина графу G величину k, залишається NP-повною задачею, якщо G береться із графів обмеженого степеня[46], планарних графів[46], планарних графів обмеженого степеня[46], хордальних графів[47], хордальних доміно[48], доповнень графів порівнянності[40], і дводольних дистанційно-успадковуваних графів[49]. Звідси негайно випливає, що задача також NP-повна для сімейств графів, що містять дводольні дистанційно-успадковувані графи, включно з дводольними графами, хордальними дводольними графами, дистанційно-успадковуваними графами та круговими графами[49].
Однак шляхову ширину можна обчислити за лінійний час для дерев і лісів[9]. Можна обчислити цю величину за поліноміальний час для графів обмеженої деревної ширини, до яких належать паралельно-послідовні графи, зовніпланарні графи і графи Халіна[50], а також розщеплювані графи[51][47], доповнення хордальних графів[52], графи перестановок[39], кографи[38], графи дуг кола[53], графи порівнянності інтервальних порядків[41] і, звичайно, самі інтервальні графи, оскільки для них шляхова ширина просто на одиницю менша від максимального числа інтервального покриття будь-якої точки в інтервальному поданні графу.
Апроксимаційні алгоритми
NP-складною задачею є апроксимація шляхової ширини графу адитивною константою[7]. Найкращий відомий апроксимаційний коефіцієнт апроксимаційних алгоритмів поліноміального часу для шляхової ширини дорівнює O((log n)3/2)[54]. Ранні апроксимаційні алгоритми для шляхової ширини можна знайти у Бодлендера, Гілберта, Хафштейнссона, Клокса[7] і Гуха[55]. Для апроксимації обмежених класів графів див. книгу Клокса і Бодлендера[51].
Мінори графу
Мінор графу G — це інший граф, створений з G стягуванням ребер, видаленням ребер і вершин. Мінор графу має глибоку теорію, в якій деякі важливі результати використовують шляхову ширину.
Виключення лісу
Якщо сімейство F графів замкнуте відносно операції взяття мінорів (будь-який мінор члена сімейства F також міститься в F), тоді за теоремою Робертсона — Сеймура сімейство F можна схарактеризувати як графи, що не містять мінорів з X, де X — скінченна множина заборонених мінорів[56]. Наприклад, теорема Вагнера стверджує, що планарні графи — це графи, які не містять ні повного графу K5, ні повного дводольного графу K3,3 як мінорів. У багатьох випадках властивості F і властивості X тісно пов'язані, і перший результат такого типу отримали Робертсон і Сеймур[2] і він пов'язує існування обмеженої шляхової ширини з наявністю лісу в сім'ї заборонених мінорів. Детальніше, визначимо сімейство F графів як таке, що має обмежену шляхову ширину, якщо існує константа p, така, що будь-який граф з F має шляхову ширину, яка не перевищує p. Тоді мінорно-замкнуте сімейство F має обмежену шляхову ширину тоді й лише тоді, коли множина X заборонених мінорів для F включає хоча б один ліс.
З одного боку, цей результат можна довести прямо — а саме, що якщо X не містить хоча б одного лісу, то вільні від X-мінорів графи не мають обмеженої шляхової ширини. В цьому випадку вільні від X-мінорів графи включають усі ліси, і зокрема досконалі бінарні дерева. Але досконалі бінарні дерева з 2k + 1 рівнями мають шляхову ширину k, так що в цьому випадку вільні від X-мінорів графи мають необмежену шляхову ширину. З іншого боку, якщо X містить ліс з n вершинами, то вільні від X-мінорів графи мають шляхову ширину, яка не перевищує n − 2[57][58][59].
Оцінки шляхової ширини

Властивість мати шляхову ширину не більше ніж p є, сама по собі, замкнутою за взяттям мінорів властивістю — якщо G має шляхову декомпозицію з шириною, що не перевищує p, то та ж сама шляхова декомпозиція залишається правильною, якщо видалити будь-яке ребро з G, а також будь-яку вершину можна видалити з графу G і його шляхової декомпозиції без збільшення ширини. Стягування ребра також можна завершити без збільшення ширини декомпозиції злиттям підшляхів, що являють собою два кінці стягуваного ребра. Таким чином, графи зі шляховою шириною, що не перевищує p, можна схарактеризувати множиною Xp заборонених мінорів[56][15][60][61].
Хоча Xp обов'язково включає щонайменше один ліс, невірно, що всі графи в Xp є лісами. Наприклад, X1 складається з двох графів, дерева з сімома вершинами і трикутника K3. Однак множину дерев у Xp можна точно описати — це точно ті дерева, які можна утворити з трьох дерев із Xp − 1 утворенням нового кореня і з'єднанням його ребрами з довільно вибраними вершинами менших дерев. Наприклад, дерево із сімома вершинами в X1 утворене з дерев з двома вершинами (одне ребро) з X0. Ґрунтуючись на цій побудові, можна показати, що число заборонених мінорів у Xp не менше від (p!)2[15][60][61]. Повну множину X2 заборонених мінорів для графів зі шляховою шириною 2 обчислено. Ця множина містить 110 різних графів[62].
Структурна теорія
Структурна теорема графів сімейств замкнутих за мінорами графів стверджує, що для будь-якого такого сімейства F, його графи можна розкласти на суму за клікою графів, які можна вкласти в поверхні обмеженого роду разом з обмеженим числом верхівок і вихорів для кожної компоненти суми за клікою. Верхівка — це вершина, яка суміжна з усіма вершинами компоненти, а вихор — це граф обмеженої шляхової ширини, що приклеюється до грані компоненти з укладенням обмеженого роду. Циклічний порядок вершин навколо грані, в яку вихор укладено, повинен бути сумісний з деревною декомпозицією вихору в тому сенсі, що розрив циклу для утворення лінійного впорядкування повинен привести до впорядкування з обмеженою величиною вершинного поділу[5]. Ця теорія, в якій шляхова ширина тісно пов'язана з довільними сімействами графів, замкнутих щодо мінорів, має важливе алгоритмічне застосування[63].
Застосування
НВІС
Під час розробки НВІС задача розділення вершин спочатку вивчалася як шлях поділу ланцюгів на менші підсистеми з малим числом компонент на межі між системами[46].
Отцукі, Морі, Кух і Кашівабара[64] використовували інтервальну товщину для моделювання числа провідників, необхідних в одновимірному розташуванні ланцюгів НВІС, утворених множиною модулів, які необхідно з'єднати системою мереж. У їхній моделі можна утворити граф, у якому вершини представляють ланцюги і в якому дві вершини з'єднано ребром, якщо їхні ланцюги приєднано до одного у того ж модуля. Тобто якщо модулі й ланцюги розуміються як вершини і гіперребра гіперграфу, то граф, утворений з них, є реберним графом гіперграфу. Інтервальне подання суперграфу цього реберного графу разом з розфарбуванням суперграфу описує розташування ланцюгів уздовж горизонтальних доріжок (одна доріжка на кожен колір), так що модулі можна розташувати вздовж доріжок у лінійному порядку і з'єднати з потрібними ланцюгами. З факту, що інтервальні графи є досконалими[65], випливає, що число кольорів, необхідних для оптимальної розкладки такого типу, дорівнює кліковому числу інтервального доповнення графу ланцюгів.
Матрична укладання перемикачів[66] є специфічним видом КМОН НВІС укладання для ланцюгів алгебри логіки. В матричних укладаннях перемикачів сигнал поширюється вздовж «ліній» (вертикальних відрізків), тоді як кожен перемикач утворюється послідовністю елементів, розташованих на горизонтальному відрізку. Таким чином, горизонтальні відрізки для кожного перемикача повинні перетинати вертикальні відрізки для кожної лінії, яка служить входом або виходом перемикача. Як і в укладаннях Отцукі, Морі, Куха і Кашівабара[64] укладання такого типу, що мінімізує число вертикальних прямих, можна знайти, обчисливши шляхову ширину графу, що має прямі як вершини, а пари прямих, що належать перемикачу, як ребра[67]. Той самий алгоритмічний підхід можна також використати для моделювання задач укладання в програмованих логічних інтегральних схемах[68][69].
Візуалізація графів
Шляхова ширина має кілька застосувань для візуалізації графів:
- Мінімальні графи, що мають задане число перетинів, мають шляхову ширину, обмежену функцією від числа перетинів[70].
- Число паралельних прямих, на яких можна розташувати вершини дерева без перетину ребер (за різних природних обмежень на способи, якими суміжні вершини можна помістити на прямих з урахуванням послідовності прямих) пропорційне шляховій ширині дерева[71].
- k-перетинний h-рівневий малюнок графу G — це розташування вершин графу G на h різних горизонтальних прямих з ребрами у вигляді монотонних (представлених ламаними) шляхів між прямими, в якому є не більше ніж k перетинів. Графи з таким поданням мають шляхову ширину, обмежену функцією від h і k. Таким чином, якщо величини h і k сталі, можна за лінійний час визначити, чи має графу k-перетинний h-рівневий малюнок[72].
- Граф з n вершинами і шляховою шириною p можна вкласти в тривимірну ґратку розміру p × p × n таким чином, що ніякі два ребра (представлені прямолінійними відрізками між точками ґратки) не перетинаються. Таким чином, графи обмеженої шляхової ширини мають вкладення цього типу з лінійним об'ємом[73].
Проєктування компіляторів
Під час трансляції високорівневих мов програмування шляхова ширина виникає в задачі переупорядкування лінійного коду (тобто без коду керувальної логіки — переходів і циклів) таким чином, що всі значення, обчислені в коді, можуть бути поміщені в машинні регістри, а не витіснені в основну пам'ять. У цьому застосуванні відтрансльований код подається у вигляді спрямованого ациклічного графу (САГ), у якому вершини представляють вхідні значення коду і значення, обчислені внаслідок операцій усередині коду. Ребро з вершини x у вершину y в цьому САГ представляє факт, що значення x є одним зі вхідних параметрів для операції y. Топологічне сортування вершин у цьому САГ представляє правильне сортування коду, а число регістрів, потрібних для виконання коду в цьому порядку задається величиною вершинного розділення впорядкування[74].
Для будь-якого фіксованого числа w регістрів у машині можна визначити за лінійний час, чи можна фрагмент лінійного коду переупорядкувати так, що для коду буде потрібно максимум w регістрів. Якщо величина вершинного топологічного розділення впорядкування не перевершує w, мінімальне вершинне розділення серед усіх впорядкувань не може бути більшим, так що неорієнтовані графи, утворені нехтууванням орієнтації САГ, описаного вище, повинні мати шляхову ширину, що не перевершує w. Можна перевірити, чи правильно це за допомогою відомих фіксовано-параметрично розв'язних алгоритмів для шляхової ширини, і, якщо правильно, знайти шляхову декомпозицію для неорієнтованих графів за лінійний час у припущенні, що w є константою. Як тільки деревну декомпозицію знайдено, топологічне сортування з шириною w (якщо таке існує) можна знайти з використанням динамічного програмування, знову ж таки за лінійний час[74].
Лінгвістика
Карнаї і Туца[75] описали застосування шляхової ширини для обробки природної мови. В цьому застосуванні речення моделюються у вигляді графів, у яких вершини представляють слова, а ребра представляють зв'язки між словами. Наприклад, якщо прикметник модифікує іменник, то граф має ребро між цими двома словами. Через обмежений обсяг короткочасної людської пам'яті Міллер[76], Корнаї і Туца стверджують, що цей граф повинен мати обмежену шляхову ширину (конкретніше, вони стверджують, що ця шляхова ширина не перевищує шести), в іншому випадку люди не могли б розпізнавати мову правильно.
Експоненційні алгоритми
Багато задачі теорії графів можна ефективно розв'язати на графах з малою шляховою шириною за допомогою динамічного програмування, спираючись на шляхову декомпозицію графу[10]. Наприклад, якщо лінійне упорядкування вершин графу G з n вершинами задано і величина вершинного розділення дорівнює w, то можна знайти найбільшу незалежну множину графу G за час O(2w n)[42]. На графі з обмеженою шляховою шириною цей підхід веде до фіксовано-параметрично розв'язних алгоритмів, параметризованих за шляховою шириною[67]. Такі результати не часто зустрічаються в літературі, оскільки вони належать до групи схожих алгоритмів, параметризованих за деревною шириною. Однак шляхова ширина з'являється навіть в алгоритмах динамічного програмування, заснованих на деревній ширині, при вимірюванні просторової складності цих алгоритмів[11].
Той самий метод динамічного програмування можна застосувати до графів з необмеженою шляховою шириною, що приводить до алгоритмів, які розв'язують непараметризовані задачі на графах за експоненційний час. Наприклад, комбінація підходу динамічного програмування з фактом, що кубічні графи мають шляхову ширину n/6 + o(n), показує, що для кубічних графів максимальну незалежну множину можна побудувати за час O(2n/6 + o(n)), що швидше від відомих до цього методів[42]. Схожий підхід веде до поліпшених алгоритмів експоненційного часу для задач максимального розрізу і мінімальної домінівної множини для кубічних графів[42] і для деяких інших NP-складних оптимізаційних задач[77][78].
Див. також
- Інтервальна розмірність графу, інший шлях вимірювання складності довільних графів у термінах інтервальних графів
- Деревна глибина — число, яке обмежене для мінорно-замкнутих сімейств графів тоді й лише тоді, коли сімейство не містить шляху
- Виродження, міра розрідженості графу, що не більша від шляхової ширини графу
- Стрічкова ширина графу, інша NP-повна задача оптимізації, яка використовує лінійні укладення графів
- Число Стралера, міра щільності кореневих дерев, що визначається подібно до шляхової ширини неорієнтованих дерев
- Деревна ширина
- Клікова ширина
,
Примітки
- Diestel, Kühn, 2005.
- Robertson, Seymour, 1983.
- Bodlaender, 1998.
- Багато використаних у статті терминів можна знайти у вступі до дисертації Ф. В. Фоміна ((Фомин, 1996))
- Robertson, Seymour, 2003.
- Kashiwabara, Fujisawa, 1979; Ohtsuki, Mori, Kuh, Kashiwabara, Fujisawa, 1979; Lengauer, 1981; Arnborg, Corneil, Proskurowski, 1987.
- Bodlaender, Gilbert, Hafsteinsson, Kloks, 1992.
- Bodlaender, 1994.
- Möhring, 1990; Scheffler, 1990; Ellis, Sudborough, Turner, 1994; Coudert, Huc, Mazauric, 1998; Peng, Ho, Hsu, Ko, Tang, 1998; Skodinis, 2000; Skodinis, (2003).
- Arnborg, 1985.
- Aspvall, Proskurowski, Telle, 2000.
- Bodlaender, 1994, с. 1–2.
- Bodlaender, 1998, с. 13, Theorem 29.
- Ellis, Sudborough, Turner, 1983.
- Kinnersley, 1992.
- Bodlaender, 1998, с. Theorem 51.
- Kirousis, Papadimitriou, 1985.
- Proskurowski, Telle, 1999.
- Korach, Solel, 1993, с. 99, Lemma 3.
- Bodlaender, 1998, с. 24, Theorem 47.
- Korach, Solel, 1993, с. 99, Lemma 1.
- Bodlaender, 1998, с. 24, Theorem 49.
- Korach, Solel, 1993, с. 99, Theorem 5.
- Bodlaender, 1998, с. 30, Theorem 66.
- Шеффлер (Scheffler, (1992)) дає сильнішу межу log3(2n + 1) шляхової ширини лісу з n вершинами.
- Korach, Solel, 1993, с. 100, Theorem 6.
- Bodlaender, 1998, с. 10, Corollary 24.
- Gurski, Wanke, 2007.
- Golovach, 1993.
- Bodlaender, 1998, с. 10, Corollary 23.
- Bodlaender, 1998, с. 9, Theorem 20.
- Alon, Seymour, Thomas, 1990.
- Bodlaender, Fomin, 2002.
- Coudert, Huc, Sereni, 2007.
- Fomin, Thilikos, 2007.
- Amini, Huc, Pérennes, 2009.
- Fomin, 2003.
- Bodlaender, Möhring, 1990.
- Bodlaender, Kloks, Kratsch, 1993.
- Habib, Möhring, 1994.
- Garbe, 1995.
- Fomin, Høie, 2006.
- Fomin, Kratsch, Todinca, Villanger, 2008.
- Downey, Fellows, 1999, с. 12.
- de Fluiter, 1997.
- Monien, Sudborough, 1988.
- Gusted, 1993.
- Kloks, Kratsch, Müller, 1995. Хордальне доміно — це хордальний граф, у якому будь-яка вершина належить максимум двом максимальним клікам
- Kloks, Bodlaender, Müller, Kratsch, 1993.
- Bodlaender, (1996); Bodlaender, Kloks, (1996)
- Kloks, Bodlaender, 1992.
- Гарбе (Garbe, (1995)) приписує цей результат тезам дисертації Тона Клокса 1993 року. Алгоритм поліноміального часу Гарбе для графів порівнянності інтервальных упорядкувань узагальнює цей результат, оскільки будь-який хордальний граф має бути графом порівнянності такого типу.
- Suchan, Todinca, 2007.
- Feige, Hajiaghayi, Lee, 2005.
- Guha, 2000.
- Robertson, Seymour, 2004.
- Bienstock, Robertson, Seymour, Thomas, 1991.
- Diestel, 1995.
- Cattell, Dinneen, Fellows, 1996.
- Takahashi, Ueno, Kajitani, 1994.
- Bodlaender, 1998, с. 8.
- Kinnersley, Langston, 1994.
- Demaine, Hajiaghayi, Kawarabayashi, 2005.
- Ohtsuki, Mori, Kuh, Kashiwabara, Fujisawa, 1979.
- Berge, 1967.
- Lopez, Law, 1980.
- Fellows, Langston, 1989.
- Möhring, 1990.
- Ferreira, Song, 1992.
- Hliněny, 2003.
- Suderman, 2004.
- Dujmović, Fellows, Kitching и др., 2008.
- Dujmović, Morin, Wood, 2003.
- Bodlaender, Gustedt, Telle, 1998.
- Kornai, Tuza, 1992.
- Miller, 1956.
- Kneis, Mölle, Richter, Rossmanith, 2005.
- Björklund, Husfeldt, 2008.
Література
- Noga Alon, Paul Seymour, Robin Thomas. Proc. 22nd ACM Symp. on Theory of Computing (STOC 1990). — 1990. — С. 293—299. — ISBN 0897913612. — DOI:10.1145/100216.100254..
- Omid Amini, Florian Huc, Stéphane Pérennes. On the path-width of planar graphs // SIAM Journal on Discrete Mathematics. — 2009. — Т. 23, вип. 3. — С. 1311—1316. — DOI:10.1137/060670146..
- Stefan Arnborg. Efficient algorithms for combinatorial problems on graphs with bounded decomposability – A survey // BIT. — 1985. — Т. 25, вип. 1. — С. 2—23. — DOI:10.1007/BF01934985..
- Stefan Arnborg, Derek G. Corneil, Andrzej Proskurowski. Complexity of finding embeddings in a $k$-tree // SIAM Journal on Algebraic and Discrete Methods. — 1987. — Т. 8, вип. 2. — С. 277—284. — DOI:10.1137/0608024..
- Bengt Aspvall, Andrzej Proskurowski, Jan Arne Telle. Memory requirements for table computations in partial k-tree algorithms // Algorithmica. — 2000. — Т. 27, вип. 3. — С. 382—394. — DOI:10.1007/s004530010025..
- Claude Berge. {{{Заголовок}}}..
- Dan Bienstock, Neil Robertson, Paul Seymour, Robin Thomas. Quickly excluding a forest // Journal of Combinatorial Theory, Series B. — 1991. — Т. 52, вип. 2. — С. 274—283. — DOI:10.1016/0095-8956(91)90068-U..
- Andreas Björklund, Thore Husfeldt. Exact algorithms for exact satisfiability and number of perfect matchings // Algorithmica. — 2008. — Т. 52, вип. 2. — С. 226—249. — DOI:10.1007/s00453-007-9149-8..
- Hans L. Bodlaender. A tourist guide through treewidth // Acta Cybernetica. — 1994. — Т. 11.
- Hans L. Bodlaender. Developments in Theoretical Computer Science (Proc. 7th International Meeting of Young Computer Scientists, Smolenice, 16–20 November 1992) / Jürgen Dassow, Alisa Kelemenová. — Gordon and Breach, 1994. — Т. 6. — С. 1—20. — (Topics in Computer Mathematics)..
- Hans L. Bodlaender. A linear-time algorithm for finding tree-decompositions of small treewidth // SIAM Journal on Computing. — 1996. — Т. 25, вип. 6. — С. 1305—1317. — DOI:10.1137/S0097539793251219..
- Hans L. Bodlaender. A partial k-arboretum of graphs with bounded treewidth // Theoretical Computer Science. — 1998. — Vol. 209, no. 1—2. — С. 1—45. — DOI:10.1016/S0304-3975(97)00228-4..
- Hans L. Bodlaender, Fedor V. Fomin. Approximation of pathwidth of outerplanar graphs // Journal of Algorithms. — 2002. — Т. 43, вип. 2. — С. 190—200. — DOI:10.1016/S0196-6774(02)00001-9..
- Hans L. Bodlaender, John R. Gilbert, Hjálmtýr Hafsteinsson, Ton Kloks. Graph-Theoretic Concepts in Computer Science. — 1992. — Т. 570. — С. 1—12. — (Lecture Notes in Computer Science). — ISBN 978-3-540-55121-8. — DOI:10.1007/3-540-55121-2_1..
- Hans L. Bodlaender, Jens Gustedt, Jan Arne Telle. Proc. 9th ACM–SIAM Symposium on Discrete Algorithms (SODA '98). — 1998. — С. 574—583..
- Hans L. Bodlaender, Ton Kloks. Efficient and constructive algorithms for the pathwidth and treewidth of graphs // Journal of Algorithms. — 1996. — Т. 21, вип. 2. — С. 358—402. — DOI:10.1006/jagm.1996.0049..
- Hans L. Bodlaender, Ton Kloks, Dieter Kratsch. Proc. 20th International Colloquium on Automata, Languages and Programming (ICALP 1993). — Springer-Verlag, 1993. — Т. 700. — С. 114—125. — (Lecture Notes in Computer Science). — ISBN 978-3-540-56939-8. — DOI:10.1007/3-540-56939-1_66..
- Hans L. Bodlaender, Rolf H. Möhring. Proc. 2nd Scandinavian Workshop on Algorithm Theory. — Springer-Verlag, 1990. — Т. 447. — С. 301—309. — (Lecture Notes in Computer Science). — ISBN 978-3-540-52846-3. — DOI:10.1007/3-540-52846-6_99..
- Kevin Cattell, Michael J. Dinneen, Michael R. Fellows. A simple linear-time algorithm for finding path-decompositions of small width // Information Processing Letters. — 1996. — Т. 57, вип. 4. — С. 197—203. — DOI:10.1016/0020-0190(95)00190-5..
- David Coudert, Florian Huc, Dorian Mazauric. Proc. 22nd Int. Symp. Distributed Computing. — Springer-Verlag, 1998. — Т. 5218. — С. 500—501. — (Lecture Notes in Computer Science). — ISBN 978-3-540-87778-3. — DOI:10.1007/978-3-540-87779-0_36..
- David Coudert, Florian Huc, Jean-Sébastien Sereni. Pathwidth of outerplanar graphs // Journal of Graph Theory. — 2007. — Т. 55, вип. 1. — С. 27—41. — DOI:10.1002/jgt.20218..
- Reinhard Diestel. Graph Minors I: a short proof of the path-width theorem // Combinatorics, Probability and Computing. — 1995. — Т. 4, вип. 1. — С. 27—30. — DOI:10.1017/S0963548300001450..
- Reinhard Diestel, Daniela Kühn. Graph minor hierarchies // Discrete Applied Mathematics. — 2005. — Т. 145, вип. 2. — С. 167—182. — DOI:10.1016/j.dam.2004.01.010..
- Erik D. Demaine, MohammadTaghi Hajiaghayi, Ken-ichi Kawarabayashi. Proc. 46th IEEE Symposium on Foundations of Computer Science (FOCS 2005). — 2005. — С. 637—646. — ISBN 0-7695-2468-0. — DOI:10.1109/SFCS.2005.14..
- Rod G. Downey, Michael R. Fellows. Parameterized Complexity. — Springer-Verlag, 1999. — ISBN 0-387-94883-X..
- V. Dujmović, M.R. Fellows, M. Kitching, G. Liotta, C. McCartin, N. Nishimura, P. Ragde, F. Rosamond, S. Whitesides, David R. Wood. On the parameterized complexity of layered graph drawing // Algorithmica. — 2008. — Т. 52, вип. 2. — С. 267—292. — DOI:10.1007/s00453-007-9151-1..
- Vida Dujmović, Pat Morin, David R. Wood. Proc. 10th International Symposium on Graph Drawing (GD 2002). — Springer-Verlag, 2003. — Т. 2528. — С. 42—53. — (Lecture Notes in Computer Science)..
- J. A. Ellis, I. H. Sudborough, J. S. Turner. Proc. 1983 Allerton Conf. on Communication, Control, and Computing. — 1983.. As cited by Monien та Sudborough, (1988).
- J. A. Ellis, I. H. Sudborough, J. S. Turner. The vertex separation and search number of a tree // Information and Computation. — 1994. — Т. 113, вип. 1. — С. 50—79. — DOI:10.1006/inco.1994.1064..
- Uriel Feige, Mohammadtaghi Hajiaghayi, James R. Lee. Proc. 37th ACM Symposium on Theory of Computing (STOC 2005). — 2005. — С. 563—572. — ISBN 1581139608. — DOI:10.1145/1060590.1060674..
- Michael R. Fellows, Michael A. Langston. Proc. 21st ACM Symposium on Theory of Computing. — 1989. — С. 501—512. — ISBN 0897913078. — DOI:10.1145/73007.73055..
- Afonso G. Ferreira, Siang W. Song. Proc. 1st Latin American Symposium on Theoretical Informatics (LATIN '92). — Springer-Verlag, 1992. — Т. 583. — С. 139—153. — (Lecture Notes in Computer Science). — ISBN 3-540-55284-7. — DOI:10.1007/BFb0023825..
- Babette de Fluiter. Algorithms for Graphs of Small Treewidth. — Utrecht University, 1997. — (Ph.D. thesis). — ISBN 90-393-1528-0..
- Fedor V. Fomin. Pathwidth of planar and line graphs // Graphs and Combinatorics. — 2003. — Т. 19, вип. 1. — С. 91—99. — DOI:10.1007/s00373-002-0490-z..
- Fedor V. Fomin, Kjartan Høie. Pathwidth of cubic graphs and exact algorithms // Information Processing Letters. — 2006. — Т. 97, вип. 5. — С. 191—196. — DOI:10.1016/j.ipl.2005.10.012..
- Fedor V. Fomin, Dieter Kratsch, Ioan Todinca, Yngve Villanger. Exact algorithms for treewidth and minimum fill-in // SIAM Journal on Computing. — 2008. — Т. 38, вип. 3. — С. 1058—1079. — DOI:10.1137/050643350..
- Fedor V. Fomin, Dimitrios M. Thilikos. On self duality of pathwidth in polyhedral graph embeddings // Journal of Graph Theory. — 2007. — Т. 55, вип. 1. — С. 42—54. — DOI:10.1002/jgt.20219..
- Renate Garbe. Proc. 20th International Workshop Graph-Theoretic Concepts in Computer Science (WG'94). — Springer-Verlag, 1995. — Т. 903. — С. 26—37. — (Lecture Notes in Computer Science). — ISBN 978-3-540-59071-2. — DOI:10.1007/3-540-59071-4_35..
- P. A. Golovach. The cutwidth of a graph and the vertex separation number of the line graph // Discrete Mathematics and Applications. — 1993. — Т. 3, вип. 5. — С. 517—522. — DOI:10.1515/dma.1993.3.5.517..
- Sudipto Guha. Proc. 41st IEEE Symposium on Foundations of Computer Science (FOCS 2000). — 2000. — С. 126. — ISBN 0-7695-0850-2. — DOI:10.1109/SFCS.2000.892072..
- Frank Gurski, Egon Wanke. Line graphs of bounded clique-width // Discrete Mathematics. — 2007. — Т. 307, вип. 22. — С. 2734—2754. — DOI:10.1016/j.disc.2007.01.020..
- Jens Gusted. On the pathwidth of chordal graphs // Discrete Applied Mathematics. — 1993. — Т. 45, вип. 3. — С. 233—248. — DOI:10.1016/0166-218X(93)90012-D..
- Michel Habib, Rolf H. Möhring. Treewidth of cocomparability graphs and a new order-theoretic parameter // Order. — 1994. — Т. 11, вип. 1. — С. 47—60. — DOI:10.1007/BF01462229..
- Petr Hliněny. Crossing-number critical graphs have bounded path-width // Journal of Combinatorial Theory, Series B. — 2003. — Т. 88, вип. 2. — С. 347—367. — DOI:10.1016/S0095-8956(03)00037-6..
- T. Kashiwabara, T. Fujisawa. Proc. International Symposium on Circuits and Systems. — 1979. — С. 657—660..
- Nancy G. Kinnersley. The vertex separation number of a graph equals its path-width // Information Processing Letters. — 1992. — Т. 42, вип. 6. — С. 345—350. — DOI:10.1016/0020-0190(92)90234-M..
- Nancy G. Kinnersley, Michael A. Langston. Obstruction set isolation for the gate matrix layout problem // Discrete Applied Mathematics. — 1994. — Т. 54, вип. 2—3. — С. 169—213. — DOI:10.1016/0166-218X(94)90021-3..
- Lefteris M. Kirousis, Christos H. Papadimitriou. Interval graphs and searching // Discrete Mathematics. — 1985. — Т. 55, вип. 2. — С. 181—184. — DOI:10.1016/0012-365X(85)90046-9.[недоступне посилання з Ноябрь 2017].
- Ton Kloks, Hans L. Bodlaender. Proc. 3rd International Symposium on Algorithms and Computation (ISAAC'92). — Springer-Verlag, 1992. — Т. 650. — С. 116—125. — (Lecture Notes in Computer Science). — ISBN 978-3-540-56279-5. — DOI:10.1007/3-540-56279-6_64..
- T. Kloks, H. Bodlaender, H. Müller, D. Kratsch. Proc. 1st European Symposium on Algorithms (ESA'93). — Springer-Verlag, 1993. — Т. 726. — С. 260—271. — (Lecture Notes in Computer Science). — DOI:10.1007/3-540-57273-2_61..
- Ton Kloks, Dieter Kratsch, H. Müller. Proc. 20th International Workshop Graph-Theoretic Concepts in Computer Science (WG'94). — Springer-Verlag, 1995. — Т. 903. — С. 106—120. — (Lecture Notes in Computer Science). — ISBN 978-3-540-59071-2. — DOI:10.1007/3-540-59071-4_41..
- Joachim Kneis, Daniel Mölle, Stefan Richter, Peter Rossmanith. Proc. 31st International Workshop on Graph-Theoretic Concepts in Computer Science (WG 2005). — Springer-Verlag, 2005. — Т. 3787. — С. 385—396. — (Lecture Notes in Computer Science). — ISBN 978-3-540-31000-6. — DOI:10.1007/11604686_34..
- Ephraim Korach, Nir Solel. Tree-width, path-width, and cutwidth // Discrete Applied Mathematics. — 1993. — Т. 43, вип. 1. — С. 97—101. — DOI:10.1016/0166-218X(93)90171-J..
- András Kornai, Zsolt Tuza. Narrowness, path-width, and their application in natural language processing // Discrete Applied Mathematics. — 1992. — Т. 36, вип. 1. — С. 87—92. — DOI:10.1016/0166-218X(92)90208-R..
- Thomas Lengauer. Black-white pebbles and graph separation // Acta Informatica. — 1981. — Т. 16, вип. 4. — С. 465—475. — DOI:10.1007/BF00264496..
- Alexander D. Lopez, Hung-Fai S. Law. A dense gate matrix layout method for MOS VLSI // IEEE Transactions on Electron Devices. — 1980. — Т. ED—27, вип. 8. — С. 1671—1675. — DOI:10.1109/T-ED.1980.20086..
- George A. Miller. The Magical Number Seven, Plus or Minus Two // Psychological Review. — 1956. — Т. 63, вип. 2. — С. 81—97. — DOI:10.1037/h0043158. — PubMed..
- Rolf H. Möhring. Computational Graph Theory / G. Tinhofer, E. Mayr, H. Noltemeier, M. Sysło. — Springer-Verlag, 1990. — Т. 7. — С. 17—51. — (Computing Supplementum). — ISBN 3-211-82177-5..
- B. Monien, I. H. Sudborough. Min cut is NP-complete for edge weighted trees // Theoretical Computer Science. — 1988. — Vol. 58, no. 1—3. — С. 209—229. — DOI:10.1016/0304-3975(88)90028-X..
- Tatsuo Ohtsuki, Hajimu Mori, Ernest S. Kuh, Toshinobu Kashiwabara, Toshio Fujisawa. One-dimensional logic gate assignment and interval graphs // IEEE Transactions on Circuits and Systems. — 1979. — Т. 26, вип. 9. — С. 675—684. — DOI:10.1109/TCS.1979.1084695..
- Sheng-Lung Peng, Chin-Wen Ho, Tsan-sheng Hsu, Ming-Tat Ko, Chuan Yi Tang. Proc. 4th Int. Conf. Computing and Combinatorics (COCOON'98). — Springer-Verlag, 1998. — Т. 1449. — С. 197—205. — (Lecture Notes in Computer Science)..
- Andrzej Proskurowski, Jan Arne Telle. Classes of graphs with restricted interval models // Theoretical Computer Science. — 1999. — Vol. 3. — С. 167—176..
- Neil Robertson, Paul Seymour. Graph minors. I. Excluding a forest // Journal of Combinatorial Theory, Series B. — 1983. — Т. 35, вип. 1. — С. 39—61. — DOI:10.1016/0095-8956(83)90079-5..
- Neil Robertson, Paul Seymour. Graph minors. XVI. Excluding a non-planar graph // Journal of Combinatorial Theory, Series B. — 2003. — Т. 89, вип. 1. — С. 43—76. — DOI:10.1016/S0095-8956(03)00042-X..
- Neil Robertson, Paul D. Seymour. Graph Minors. XX. Wagner's conjecture // Journal of Combinatorial Theory, Series B. — 2004. — Т. 92, вип. 2. — С. 325—357. — DOI:10.1016/j.jctb.2004.08.001..
- Petra Scheffler. Topics in Combinatorics and Graph Theory / R. Bodendiek, R. Henn. — Physica-Verlag, 1990. — С. 613—620..
- Petra Scheffler. Fourth Czechoslovakian Symposium on Combinatorics, Graphs and Complexity / Jaroslav Nešetřil, Miroslav Fiedler. — Elsevier, 1992..
- Konstantin Skodinis. Proc. 8th European Symposium on Algorithms (ESA 2000). — Springer-Verlag, 2000. — Т. 1879. — С. 403—414. — (Lecture Notes in Computer Science). — ISBN 978-3-540-41004-1. — DOI:10.1007/3-540-45253-2_37..
- Konstantin Skodinis. Construction of linear tree-layouts which are optimal with respect to vertex separation in linear time // Journal of Algorithms. — 2003. — Т. 47, вип. 1. — С. 40—59. — DOI:10.1016/S0196-6774(02)00225-0..
- Karol Suchan, Ioan Todinca. Proc. 33rd International Workshop on Graph-Theoretic Concepts in Computer Science (WG 2007). — Springer-Verlag, 2007. — Т. 4769. — С. 258—269. — (Lecture Notes in Computer Science). — DOI:10.1007/978-3-540-74839-7_25..
- Matthew Suderman. Pathwidth and layered drawings of trees // International Journal of Computational Geometry and Applications. — 2004. — Т. 14, вип. 3. — С. 203—225. — DOI:10.1142/S0218195904001433..
- Atsushi Takahashi, Shuichi Ueno, Yoji Kajitani. Minimal acyclic forbidden minors for the family of graphs with bounded path-width // Discrete Mathematics. — 1994. — Т. 127, вип. 1—3. — С. 293—304. — DOI:10.1016/0012-365X(94)90092-2..
- Ф.В. Фомин. Задачи преследования и поиска на графах // Электронная библиотека диссертаций. — 1996.