Паралельно-послідовний граф

В теорії графів паралельно-послідовні графи — це графи з двома різними вершинами, які називаються термінальними, утворені рекурсивно за допомогою двох простих операцій[1]. Ці графи можна використати для моделювання послідовного і паралельного з'єднання ділянок електричних кіл.

Операції послідовного і паралельного з'єднання в послідовно-паралельних графах.

Визначення та термінологія

В даному контексті поняття граф передбачає мультиграф.

Існує декілька способів визначення паралельно-послідовних графів. Таке визначення, переважно, базується на визначенні Девіда Еппштейна[2].

Графом з однією термінальною парою (ОТП) називається граф, у якого позначено дві різні вершини s і t, звані джерелом і стоком відповідно.

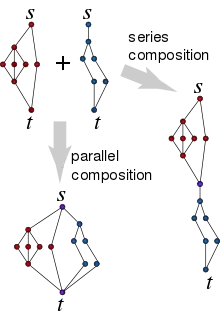
Паралельне з'єднання Pc = Pc(X, Y) двох ОТП графів X і Y, що не перетинаються — це граф з однією термінальною парою, створений об'єднанням графів X і Y за допомогою злиття джерел X і Y з утворенням джерела Pc і злиттям стоків X і Y з утворенням стоку графу Pc.

Послідовне з'єднання Sc = Sc(X, Y) двох ОТП графів X і Y, що не перетинаються — це ОТП-граф, створений об'єднанням графів X і Y шляхом злиття стоку X з джерелом Y. Джерело графу X стає джерелом Sc, а стік графу Y стає стоком Sc.

Паралельно-послідовний граф з однією термінальною парою (ППОТП граф) — це граф, який можна отримати послідовно і паралельно з'єднуючи множину копій однореберних графів K2 з призначеними термінальними вершинами.

Визначення 1. Граф називається послідовно-паралельним, якщо він ППОТП і дві його вершини позначено як джерело і стік.

Так само можна визначити послідовно-паралельні орграфи, які будуються з копій орієнтованих графів з однією дугою, і в цьому випадку дуга спрямована із джерела в стік.

Альтернативне визначення

Таке визначення дає той самий клас графів[3].

Визначення 2. Граф є послідовно-паралельним, якщо його можна перетворити на граф K2 послідовністю таких операцій:

  • Замінюємо пару паралельних ребер одним ребром, зберігаючи спільні кінцеві вершини
  • Замінюємо пару ребер, інцидентних ребру степеня 2 одним ребром.

Властивості

Будь-який паралельно-послідовний граф має деревну ширину і ширину галуження, які не перевищують 2[4]. Насправді граф має деревну ширину не більше 2 тоді й лише тоді, коли він має ширину галуження максимум 2, а також тоді й лише тоді, коли будь-яка двозв'язна компонента є паралельно-послідовним графом[5][6]. Максимальні паралельно-послідовні графи, графи, до яких можна додати додаткові ребра без руйнування послідовно-паралельної структури, — це точно 2-дерева.

Паралельно-послідовні графи характеризуються відсутністю підграфу, гомеоморфного графу K4[4].

Паралельно-послідовні графи можна схарактеризувати їхнім вушним розкладом[2].

Дослідження, з застосуванням паралельно-послідовних графів

Паралельно-послідовні графи можна розпізнати за лінійний час[7] та їх паралельно-послідовні розклади можна побудувати також за лінійний час.

Крім моделювання деяких типів електричних кіл, ці графи становлять інтерес у теорії обчислювальної складності, оскільки багато стандартних задач на графах розв'язуються за лінійний час на ОТП-графах[8], зокрема пошук найбільшого парування, найбільшої незалежної множини, найменшої домінівної множини і гамільтонового доповнення. Деякі з цих задач для графів загального вигляду NP-повні. Причиною цього є факт, що якщо відповіді для цих задач відомі для двох паралельно-послідовних графів, то можна швидко знайти відповідь для їх послідовних і паралельних з'єднань.

Задача про послідовно-паралельні графи стосується питання перерахування графів і запитує про число паралельно-послідовних графів, які можна утворити із заданого числа ребер.

Узагальнення

Узагальнені паралельно-послідовні графи (УПП-графи) — це узагальнення паралельно-послідовних графів[9], за якого графи мають таку ж алгоритмічну ефективність для згаданих задач. Клас УПП-графів включає паралельно-послідовні графи і зовніпланарні графи .

УПП-графи можна визначити доданням у Визначення 2 третьої операції видалення висячих вершин (вершин степеня 1). Таким само до Визначення 1 можна додати таку операцію.

  • Злиття джерел S = M (X, Y) двох ОТП-графів X і Y — це ОТП-граф, створений з графів X і Y, що не перетинаються, злиттям джерела X із джерелом Y. Джерело і стік графу X стає джерелом і стоком P відповідно.

SPQR-дерево — це структура, яку можна визначити для довільного 2-вершинно-зв'язного графу. Структура має S-вузли, аналогічні послідовному з'єднанню в паралельно-послідовних графах, P-вузли, аналогічні паралельному з'єднанню паралельно-послідовних графів і R-вузли, які не відповідають операціям паралельно-послідовних графів. 2-зв'язний граф є паралельно-послідовним тоді й лише тоді, коли в дереві SPQR немає R-вузлів.

Див. також

Примітки
  1. Свами, Тхуласираман, 1984, с. 150, Упражнение 7.10.
  2. Eppstein, 1992, с. 41–55.
  3. Duffin, 1965, с. 303–313.
  4. Brandstädt, Le, Spinrad, 1999, с. 172-174.
  5. Bodlaender, 1998, с. 1–45.
  6. Hall, Oxley, Semple, Whittle, 2002, с. 148–171.
  7. Valdes, Tarjan, Lawler, 1982, с. 289–313.
  8. Takamizawa, Nishizeki, Saito, 1982, с. 623–641.
  9. Корниенко, 1984, с. 109-111.

Література
  • М. Свами, К. Тхуласираман. Графы, сети и алгоритмы. — М. : «Мир», 1984.
  • Jacobo Valdes, Robert E. Tarjan, Eugene L. Lawler. The recognition of series parallel digraphs // SIAM Journal on Computing. — 1982. — Т. 11, вип. 2 (3 листопада). — DOI:10.1137/0211023.
  • Н.М. Корниенко. Комбинаторные алгоритмы на классе графов // Известия Национальной академии наук Беларуси СЕРИЯ ФИЗИКО-ТЕХНИЧЕСКИХ НАУК. — 1984. — Вип. 3 (3 листопада). — С. 109-111.
  • David Eppstein. Parallel recognition of series-parallel graphs // Information and Computation. — 1992. — Т. 98, вип. 1 (3 листопада). — С. 41–55. — DOI:10.1016/0890-5401(92)90041-D.
  • R. J. Duffin. Topology of Series-Parallel Networks // Journal of Mathematical Analysis and Applications. — 1965. — Т. 10, вип. 2 (3 листопада). — С. 303–313. — DOI:10.1016/0022-247X(65)90125-3.
  • Andreas Brandstädt, Van Bang Le, Jeremy P. Spinrad. Graph classes: a survey. — Philadelphia, PA : Society for Industrial and Applied Mathematics, 1999. — Т. 3. — С. 172-174. — (SIAM Monographs on Discrete Mathematics. and Applications) — ISBN 978-0-898714-32-6.
  • H. Bodlaender. A partial k-arboretum of graphs with bounded treewidth // Theoretical Computer Science. — 1998. — Т. 209, вип. 1–2 (3 листопада). — С. 1–45. — DOI:10.1016/S0304-3975(97)00228-4.
  • Rhiannon Hall, James Oxley, Charles Semple, Geoff Whittle. On matroids of branch-width three // Journal of Combinatorial Theory, Series B. — 2002. — Т. 86, вип. 1 (3 листопада). — С. 148–171. — DOI:10.1006/jctb.2002.2120.
  • K. Takamizawa, T. Nishizeki, N. Saito. Linear-time computability of combinatorial problems on series-parallel graphs // Journal of the ACM. — 1982. — Т. 29, вип. 3 (3 листопада). — С. 623–641. — DOI:10.1145/322326.322328.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.