Тривіально досконалий граф

Тривіально досконалі графи мають кілька інших еквівалентних описів:

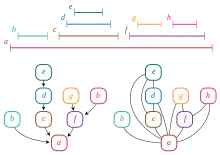
• Вони є графами порівнянності дерев з теорії порядків. Тобто, нехай T — частковий порядок, такий, що для будь-якого t ∈ 'T' множина {s ∈ T : S < t} є цілком упорядкованою з відношенням < і T має найменший елемент r. Тоді граф порівнянності порядку T тривіально досконалий і будь-який тривіально досконалий граф можна сформувати таким способом[7][8].
• Вони є графами, що не містять шляху P₄ або циклу C₄ як породжених підграфів[7][9][10]
• Вони є графами, в яких кожен зв'язний породжений підграф містить універсальну вершину[3].
• Вони є графами, які можна подати як інтервальні графи множини вкладених проміжків. Множина проміжків має властивість вкладеності, якщо для будь-яких двох проміжків із множини вони або не перетинаються, або один з них міститься в іншому[11].
• Вони є графами, які одночасно є хордальними графами і кографами[12][13]. Це випливає з опису хордальних графів як графів без породжених циклів довжини чотири і більше і кографів як графів без породжених шляхів з чотирма вершинами (P₄).
• Це графи, які водночас є кографами й інтервальними графами[12][13].
• Вони є графами, які можна утворити, починаючи з графів з однією вершиною, за допомогою двох операцій — незв'язного об'єднання двох менших тривіально досконалих графів і додання нової вершини, суміжної всім вершинам меншого тривіально досконалого графу[6][14]. Ці операції відповідають утворенню нового лісу незв'язним об'єднанням двох менших лісів і утворенню дерева з'єднанням нового кореня з коренями всіх дерев лісу.
• Вони є графами, в яких для будь-якого ребра uv околи вершин u і v (включно з самими u і v) вкладені — один окіл має бути околом іншого[13].
• Вони є графами перестановки, визначеними зі сортованих у стеку перестановок[15].
• Вони є графами з властивістю, що в кожному його породженому підграфі число клікового покриття дорівнює числу максимальних клік[16].
• Вони є графами з властивістю, що в кожному його породженому підграфі клікове число дорівнює псевдочислу Ґранді[16].
• Вони є графами з властивістю, що хроматичне число кожного його породженого підграфу дорівнює псевдочислу Ґранді[16].

З еквівалентних описів тривіально досконалих графів випливає, що будь-який тривіально досконалий граф є також кографом, хордальним, птолемеєвим, інтервальним і досконалим графом.

Порогові графи — це точно ті графи, які є одночасно тривіально досконалими і є доповненням тривіально досконалих графів (тривіально досконалих кографів)[17][18].

Вітряки є тривіально досконалими.

Чу[19] описує простий алгоритм лінійного часу для розпізнавання тривіально досконалих графів, заснований на лексикографічному пошуку в ширину. Коли алгоритм LexBFS видаляє вершину v з першої множини в черзі, алгоритм перевіряє, що всі сусіди вершини v, що залишилися, належать тій самій множині. Якщо ні, один із заборонених породжених підграфів можна побудувати з v. Якщо перевірка успішна для всіх v, то граф тривіально досконалий. Алгоритм можна модифікувати для перевірки за лінійний час, чи є граф доповненням тривіально досконалого графу.

Визначення, чи стає граф загального вигляду після видалення k ребер тривіально досконалим графом, є NP-повною задачею[20], фіксовано-параметрично розв'язною[21], і її можна розв'язати за час O(2,45^k(m+n))[22].

• Trivially perfect graphs. Information System on Graph Classes and their Inclusions.