Десятковий логарифм

У нижченаведеній таблиці передбачається, що всі значення позитивні [1]:

	Формула	Приклад
Добуток	${\displaystyle \lg(xy)=\lg(x)+\lg(y)\,}$	${\displaystyle \lg(10000)=\lg(100\cdot 100)=\lg(100)+\lg(100)=2+2=4\,}$
Частка від ділення	${\displaystyle \lg \!\left({\frac {x}{y}}\right)=\lg(x)-\lg(y)\,}$	${\displaystyle \lg \left({\frac {1}{1000}}\right)=\lg(1)-\lg(1000)=0-3=-3}$
Степінь	${\displaystyle \lg(x^{p})=p\lg(x)\,}$	${\displaystyle \lg(10000000)=\lg(10^{7})=7\lg(10)=7\,}$
Корінь	${\displaystyle \lg {\sqrt[{p}]{x}}={\frac {\lg(x)}{p}}\,}$	${\displaystyle \lg {\sqrt {1000}}={\frac {1}{2}}\lg 1000={\frac {3}{2}}=1{,}5}$

Існує очевидне узагальнення наведених формул на випадок, коли допускаються негативні змінні, наприклад:

${\displaystyle \lg |xy|=\lg(|x|)+\lg(|y|),}$

${\displaystyle \lg \!\left|{\frac {x}{y}}\right|=\lg(|x|)-\lg(|y|),}$

Формула для логарифма добутку легко узагальнюється на довільну кількість співмножників:

${\displaystyle \lg(x_{1}x_{2}\dots x_{n})=\lg(x_{1})+\lg(x_{2})+\dots +\lg(x_{n})}$

Вищеописані властивості пояснюють, чому застосування логарифмів (до винаходу калькуляторів) істотно полегшувало обчислення. Наприклад, множення багатозначних чисел ${\displaystyle x,y}$ за допомогою логарифмічних таблиць ^[⇨] вироблялося за наступним алгоритмом:

1. Знайти в таблицях логарифми чисел ${\displaystyle x,y}$.
2. Скласти ці логарифми, отримуючи (відповідно до першої властивості) логарифм добутку ${\displaystyle x\cdot y}$.
3. За логарифмом добутку знайти в таблицях сам добуток.

Ділення, яке без допомоги логарифмів набагато трудомісткіше, ніж множення, виконувалося за тим же алгоритмом, лише із заміною складання логарифмів — відніманням. Аналогічно здійснювалися піднесення до степеня і знаходження кореня.

Зв'язок десяткового і натурального логарифмів [2]:

${\displaystyle \ln x\approx 2{,}30259\ \lg x;\quad \lg x\approx 0{,}43429\ \ln x}$

Знак логарифма залежить від логарифмуємого числа: якщо воно більше 1, логарифм позитивний, якщо воно між 0 і 1, то від'ємний. Приклад:

${\displaystyle \lg \,0{,}012=\lg \,(10^{-2}\times 1{,}2)=-2+\lg \,1{,}2\approx -2+0{,}079181=-1{,}920819}$

Щоб уніфікувати дії з позитивними і негативними логарифмами, в останніх ціла частина (характеристика) надкреслюється зверху:

${\displaystyle \lg \,0{,}012\approx -2+0{,}079181={\bar {2}}{,}079181}$

Мантиса логарифма, обрана з таблиць, при такому підході завжди позитивна.

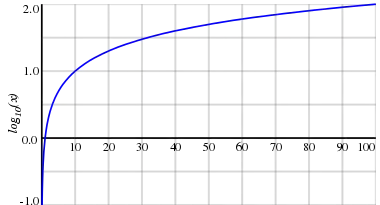
Якщо розглядати логарифмуєме число як змінну, ми отримаємо функцію десяткового логарифма: ${\displaystyle ~y=\lg \,x.}$. Вона визначена при всіх ${\displaystyle ~x>0.}$ Область значень: ${\displaystyle E(y)=(-\infty$ ;+\infty )} . Графік цієї кривої часто називається логарифмікою[3].

Функція монотонно зростає, неперервна і диференційована усюди, де вона визначена. Похідна для неї знаходиться за формулою:

${\displaystyle {\frac {d}{dx}}\lg \,x={\frac {\lg \,e}{x}}}$

Вісь ординат ${\displaystyle (x=0)}$ є лівою вертикальною асимптотою, оскільки:

${\displaystyle \lim _{x\to 0+0}\lg \,x=-\infty }$

Логарифми за основою 10 до винаходу в 1970-і роки компактних електронних калькуляторів широко застосовувалися для обчислень. Як і будь-які інші логарифми, вони дозволяли багаторазово спростити і полегшити трудомісткі розрахунки, замінюючи множення на додавання, а ділення на віднімання; аналогічно спрощувались піднесення до степеня і знаходження кореня. Але десяткові логарифми мали перевагу перед логарифмами за іншою основою: цілу частину ${\displaystyle L}$ логарифма числа ${\displaystyle x}$ (характеристику логарифма) легко визначити.

• Якщо ${\displaystyle x>1,}$ то ${\displaystyle L}$ на 1 менше числа цифр в цілій частині числа ${\displaystyle x}$. Наприклад, відразу очевидно, що lg 345 знаходиться в проміжку (2, 3).
• Якщо ${\displaystyle x<1,}$ то найближче до ${\displaystyle L}$ ціле (в меншу сторону) дорівнює загальній кількості нулів в ${\displaystyle x}$ перед першою ненульовий цифрою, взятому зі знаком мінус. Наприклад, lg 0,0014 знаходиться в інтервалі (-3, -2).

Крім того, при перенесенні десяткової коми в числі на ${\displaystyle n}$ розрядів значення десяткового логарифма цього числа змінюється на ${\displaystyle n.}$ Наприклад:

${\displaystyle \lg 8314{,}63=\lg 8{,}31463+3}$

Звідси випливає, що досить скласти таблицю мантис (дробових частин) десяткових логарифмів для чисел в діапазоні від 1 до 10. Такі таблиці, починаючи з XVII століття, випускалися великим тиражем і служили незамінним розрахунковим інструментом вчених та інженерів.

Оскільки застосування логарифмів для розрахунків з появою обчислювальної техніки майже припинилося, в наші дні десятковий логарифм в значній мірі витіснений натуральним [4]. Він зберігається в основному в тих математичних моделях, де історично вкоренився — наприклад, при побудові логарифмічних шкал.

Зверніть увагу, що у всіх наведених у таблиці чисел одна і та ж мантиса.

Десяткова логарифмічна шкала на логарифмічній лінійці

Перші таблиці десяткових логарифмів опублікував в 1617 році оксфордський професор математики Генрі Брігс для чисел від 1 до 1000, з вісьмома (пізніше — з чотирнадцятьма) знаками. Тому за кордоном десяткові логарифми часто називають брігсовимі. Але в цих і в наступних виданнях таблиць виявилися помилки. Перше безпомилкове видання на основі таблиць Георга Веги (1783) з'явилося тільки в 1857 в Берліні (таблиці Бремікера, Carl Bremiker) [5].

У Росії перші таблиці логарифмів були видані в 1703 році за участю Л. П. Магницького[6]. У СРСР випускалися кілька збірок таблиць логарифмів[7]:

1. Брадис В. М. Чотиризначні математичні таблиці. М.: Дрофа, 2010, ISBN 978-5-358-07433-0. Таблиці Брадиса, що видаються з 1921 року, використовувалися в навчальних закладах та в інженерних розрахунках, що не вимагають великої точності. Вони містили мантиси десяткових логарифмів чисел і тригонометричних функцій, натуральні логарифми і деякі інші корисні розрахункові інструменти.
2. Вега Г. Таблиці семизначних логарифмів, 4-е видання, М.: Надра, 1971. Професійний збірник для точних обчислень.

• Выгодский М. Я. Справочник по элементарной математике. — изд. 25-е. — М.: Наука, 1978. — ISBN 5-17-009554-6.
• Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с.