Джино Фано

Джино Фано[4] (5 січня 1871 – 8 листопада 1952) — італійський математик, найбільш відомий як засновник скінченної геометрії. Народився в заможній єврейській[5] сім'я в Мантуї, в Італії і помер у Вероні, в Італії.

Джино Фано
Народився 5 січня 1871(1871-01-05)[1][2][…]
Мантуя, Ломбардія, Королівство Італія[3]
Помер 8 листопада 1952(1952-11-08)[1][2][…] (81 рік)
Верона, Венето, Італія[1][3]
Країна  Італія
 Королівство Італія
Діяльність математик
Alma mater Туринський університет
Галузь математика
Заклад Туринський університет, Римський університет ла Сапієнца[2] і Університет Мессіниd
Науковий керівник Корадо Сегреd
Членство Туринська академія наук[3] і National Virgilian Academyd
Діти Уго Фано і Роберт Фано
 Джино Фано у Вікісховищі

У 1888 році вступив в Туринський університет, де був учнем Сегре Коррадо і Гвідо Кастельнуово. У 1893—1894 роках відвідував лекції Фелікса Кляйна в Геттінгені (ще до цього Фано перевів знамениту Ерлангенську програму Клейна на італійську мову). До 1899 року Фано був асистентом Кастельнуово в Римі, після чого отримав посаду професора в університеті Мессіни, а потім в Туринському університеті. У 1938 році він був змушений покинути цей пост через переслідування фашистського режиму і переїхав до Швейцарії. Після закінчення війни продовжував читати лекції в Італії, а також в Сполучених Штатах. Був обраний членом Національної академії деї Лінчеї.

Фано зробив значний внесок в проєктивну[6] і алгебраїчну геометрію. Його робота з основ геометрії передує аналогічній, але більш популярній, роботі Давида Гільберта приблизно на десять років.

Джино Фано був батьком фізика Уго Фано і електротехніка Роберта Фано та дядьком фізика і математика Джуліо Рака.

Математичні роботи

Фано був раннім автором в області кінцевих проективних просторів. У своїй статті[7] про доказ незалежності свого набору аксіом для проективного n-простору,[8] він розглядав, крім іншого, наслідки наявності четвертої четвертої гармонічної точки рівної її сполученому. Це призводить до конфігурації семи точок і семи ліній, що містяться в кінцевому тривимірному просторі з 15 точками, 35 лініями і 15 площинами, з яких кожна лінія містила тільки три точки.[7]:114

Всі площини в цьому просторі складаються з семи точок і семи ліній і тепер відомі як площина Фано:

Fano Plane (7 points and 7 lines)

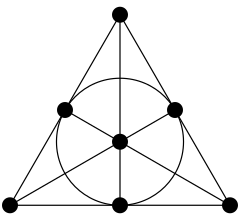
Фано продовжив опис кінцевих проективних просторів довільних розмірів і первинних порядків.

У 1907 році Джино Фано написав дві статті до третьої частини енциклопедії Кляйна. Першою статтею (с. 221—288) було порівняння аналітичної геометрії та синтетичної геометрії на основі їх історичного розвитку в 19 столітті. Другою (с. 282—388) була стаття про топологічні групи і теорію груп в геометрії, як об'єднувальний принцип у галузі геометрії.

Примітки
  1. Німецька національна бібліотека, Державна бібліотека в Берліні, Баварська державна бібліотека та ін. Record #116407913 // Німецька нормативна база даних — 2012—2016.
  2. Архів історії математики Мактьютор
  3. Туринська академія наук — 1757.
  4. Фано Джино. persons-info.com. Процитовано 4 березня 2019.
  5. Carroll, Maureen T.; Rykken, Elyn (2018). Geometry: The Line and the Circle. American Mathematical Society. с. 336. «Gino Fano came from a wealthy Jewish family in Mantua, Italy.»
  6. Ellenberg, Jordan (25 жовтня 2017). Як ніколи не помилятися: Сила математичного мислення (англ.). Nash Format. ISBN 9786177513413.
  7. Fano, G. (1892). Sui postulati fondamentali della geometria proiettiva. Giornale di Matematiche 30: 106–132.
  8. Collino, Conte & Verra, 2013

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.