Аналітична геометрія

Ілюстрація декартової системи координат. Чотири відмічені точки позначені їх координатами: (2,3) зеленим, (−3,1) червоним, (−1.5,−2.5) синім, і початок координат (0,0) пурпуровим.

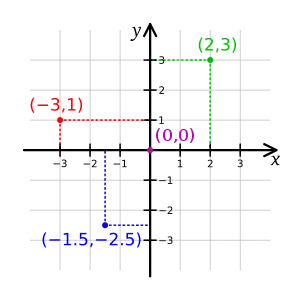
В аналітичній геометрії, двовимірний простір задається системою координат, в якій кожна точка маж пару координат у формі дійсних чисел. Аналогічним чином, Евклідів простір представлено координатами, де кожна точка має три координати. Значення координат залежить від вибору точки початкового відліку. Існує велика кількість різних систем координат, але найбільш загальними є наступні:[4]

Характерною особливістю аналітичної геометрії є визначення геометричних фігур рівняннями. Нехай на площині з осями координат OX і OY (прямокутна декартова система координат) маємо лінію l. Якщо вздовж l пересувати точку M, то координати x, y цієї точки будуть змінюватись, але між ними існуватиме певна залежність, яку можна записати у вигляді рівняння:

${\displaystyle f(x,y)=0\,}$,

де ${\displaystyle f(x,y)}$ є математичний вираз, що містить змінні x і y або одну з них.

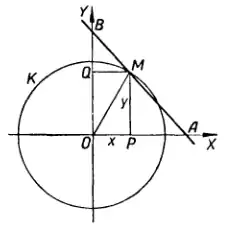
Наприклад, з прямокутного трикутника OMP виводимо, що рівняння кола K радіуса г з центром в початку координат 0 є

${\displaystyle x^{2}+y^{2}-r^{2}=0}$.

Розглянемо ще пряму АВ. Якщо М є довільна її точка і OA = a, OB = b, то PA = a — x. З подібності прямокутних трикутників MPA і BOA маємо:

${\displaystyle {\frac {y}{a-x}}={\frac {b}{a}}}$.

Звідси дістаємо рівняння прямої АВ:

${\displaystyle bx+ay-ab=0\,}$.

В аналітичній геометрії приймають, що рівняння визначає геометричну фігуру як множину точок, координати х та у яких справджують це рівняння. Інакше кажучи, рівняння розглядають як засіб для поділу точок площини на 2 класи: до 1-го належать точки, координати яких справджують дане рівняння (ці точки утворюють визначену рівнянням фігуру), до 2-го — всі інші точки площини. Якщо рівняння алгебраїчне, то воно визначає лінію — дійсну чи уявну (див. нижче), яку називають алгебраїчною, а степінь рівняння — порядком цієї лінії. Порядок алгебраїчної лінії не залежить від того, як розміщені відносно неї осі координат. Прямі і тільки прямі є лініями 1-го порядку; конічні перерізи (тобто лінії, що утворюються при перетині конуса площиною) і тільки вони є лініями 2-го порядку. Аналогічно рівняння ${\displaystyle f(x,y,z)=0}$, де ${\displaystyle x,y,z}$ — декартові координати точки у просторі, визначає просторову фігуру, зокрема алгебраїчну поверхню n-го порядку, якщо воно є алгебраїчним рівнянням n-го степеня. В сучасних курсах аналітичної геометрії вивчаються тільки лінії і поверхні 1-го та 2-го порядків.

Застосування в аналітичній геометрії алгебраїчних методів привело до поняття уявної фігури. Сукупність двох чисел ${\displaystyle x,y,}$ з яких принаймні одне уявне, можна розглядати як уявну точку. Якщо рівняння (наприклад , ${\displaystyle x^{2}+y^{2}+1=0}$) справджують лише координати уявних точок, то вважають, що воно визначає уявну фігуру. Хоч поняттям нескінченно віддалених і уявних точок не відповідають жодні реальні образи, проте запровадження їх дозволило глибше досліджувати властивості фігур.

В сучасних курсах аналітичної геометрії широко використовується апарат векторного числення.

Формула відстані на площині слідує із теореми Піфагора.

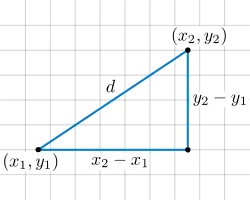
В аналітичній геометрії, геометричні поняття такі як міри відстані і кута визначають за допомогою формул. Ці визначення узгоджені із Евклідовою геометрією, яка є в основі них. Наприклад, при використанні Декартових координат на площині, відстань між двома точками (x₁, y₁) і (x₂, y₂) визначається формулою

${\displaystyle d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}},}$

яку можна розглядати як ще одну версію теореми Піфагора. Аналогічно, кут, який пряма утворює із горизонталлю можна визначити за допомогою формули

${\displaystyle \theta =\mathrm {arctg} (m),}$

де m це нахил (кутовий коефіцієнт) прямої.

В трьох вимірах, відстань визначається за допомогою узагальненої теореми Піфагора:

${\displaystyle d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}},}$

а кут між двома векторами задається скалярним добутком. Скалярний добуток двох Евклідових векторів A і B визначається як[5]

${\displaystyle \mathbf {A} \cdot \mathbf {B} {\stackrel {\mathrm {def} }{=}}\|\mathbf {A} \|\,\|\mathbf {B} \|\cos \theta ,}$

де θ це кут між A і B.

a) y = f(x) = |x|       b) y = f(x+3)       c) y = f(x)-3       d) y = 1/2 f(x)

Перетворення застосовуються до початкової функції з метою перетворити її на нову функцію із подібними характеристиками.

Графік функції ${\displaystyle R(x,y)}$ змінюється за допомогою стандартних перетворень наступним чином:

• Зміна ${\displaystyle x}$ на ${\displaystyle x-h}$ переміщає графік праворуч на ${\displaystyle h}$ одиниць.
• Зміна ${\displaystyle y}$ на ${\displaystyle y-k}$ переміщає графік вгору на ${\displaystyle k}$ одиниць.
• Зміна ${\displaystyle x}$ на ${\displaystyle x/b}$ розтягує графік функції по горизонталі на величину коефіцієнта ${\displaystyle b}$. (вважаємо що ${\displaystyle x}$ було розширено)
• Зміна ${\displaystyle y}$ на ${\displaystyle y/a}$ розтягує графік вертикально.
• Зміна ${\displaystyle x}$ на ${\displaystyle x\cos A+y\sin A}$ і зміна ${\displaystyle y}$ на ${\displaystyle -x\sin A+y\cos A}$ обертає графік на кут ${\displaystyle A}$.

Існують і інші стандартні перетворення, які як правило не вивчаються в рамках елементарної аналітичної геометрії, оскільки перетворення змінюють форму об'єктів у такий спосіб, який не розглядається часто. Наприклад, таким перетворенням є перетворення скосу.

Наприклад, початкова функція ${\displaystyle y=1/x}$ має горизонтальну і вертикальну асимптоту, і займає перший і другий квадрант, і всі форми її перетворення мають горизонтальну і вертикальну асимптоту, і займають або 1-й і 3-й або 2-й і 4-й квадрант. В загальному випадку, якщо дана функція ${\displaystyle y=f(x)}$, то її можна трансформувати у вигляд ${\displaystyle y=af(b(x-k))+h}$. В новій перетвореній функції, ${\displaystyle a}$ це коефіцієнт вертикального розтягування функції, якщо він більший за 1, або вертикального стискання, якщо він менший за 1, а для від'ємних значень ${\displaystyle a}$, функція буде відображена по осі ${\displaystyle x}$. Коефіцієнт ${\displaystyle b}$ стискає графік функції по горизонталі, якщо він більший за 1 і розтягує функцію горизонтально, якщо він менший за 1, і так само як ${\displaystyle a}$, відображає функцію по осі ${\displaystyle y}$, коли він від'ємний. Значення ${\displaystyle k}$ і ${\displaystyle h}$ задають переміщення, ${\displaystyle h}$ — вертикальне, і ${\displaystyle k}$ — горизонтальне. Додатні значення ${\displaystyle h}$ і ${\displaystyle k}$ означають, що функція переміщується в додатному напрямку відповідної осі, а від'ємне значення, що вона переміщується в сторону від'ємного напрямку.

Перетворення можна застосувати до будь-якого геометричного рівняння, не залежно від того чи задає це рівняння функцію, чи ні.

Для двох геометричних об'єкта P і Q, які представлені рівняннями ${\displaystyle P(x,y)}$ і ${\displaystyle Q(x,y)}$ перетином є набір всіх таких точок ${\displaystyle (x,y)}$, які відповідають двом рівнянням одночасно.

Наприклад, ${\displaystyle P}$ може бути колом із радіусом 1 і з центром в координатах ${\displaystyle (0,0)}$: ${\displaystyle P=\{(x,y)|x^{2}+y^{2}=1\}}$, а ${\displaystyle Q}$ може бути колом із радіусом 1 і центром в ${\displaystyle (1,0):Q=\{(x,y)|(x-1)^{2}+y^{2}=1\}}$. Перетином цих кіл є множина точок, при якій обидва рівняння виконуються. Чи точка з координатами ${\displaystyle (0,0)}$ робить обидва ці рівняння вірними? Підставивши ${\displaystyle (0,0)}$ для ${\displaystyle (x,y)}$, рівняння для ${\displaystyle Q}$ буде наступним ${\displaystyle (0-1)^{2}+0^{2}=1}$ або ${\displaystyle (-1)^{2}=1}$, що є вірним, тож ${\displaystyle (0,0)}$ відповідає рівнянню ${\displaystyle Q}$. З іншого боку, використавши ${\displaystyle (0,0)}$ для ${\displaystyle (x,y)}$ в рівнянні ${\displaystyle P}$ отримаємо ${\displaystyle 0^{2}+0^{2}=1}$ або ${\displaystyle 0=1}$, що є хибним. ${\displaystyle (0,0)}$ не належить ${\displaystyle P}$, то ж ця точка не є перетином.

Перетин фігур ${\displaystyle P}$ і ${\displaystyle Q}$ можна знайти розв'язавши одночасні рівняння:

${\displaystyle x^{2}+y^{2}=1}$

${\displaystyle (x-1)^{2}+y^{2}=1.}$

Традиційними методами пошуку перетинів за допомогою таких рівнянь є заміна і скорочення.

Метод заміни: (метод підстановки) Необхідно розв'язати рівняння відносно ${\displaystyle y}$, спочатку виразимо його через ${\displaystyle x}$, а потім підставляємо отриманий вираз для ${\displaystyle y}$ в друге рівняння:

${\displaystyle x^{2}+y^{2}=1}$

${\displaystyle y^{2}=1-x^{2}}$.

Потім, після підстановки отриманого значення для ${\displaystyle y^{2}}$ в інше рівняння, маємо розв'язок для ${\displaystyle x}$:

${\displaystyle (x-1)^{2}+(1-x^{2})=1}$

${\displaystyle x^{2}-2x+1+1-x^{2}=1}$

${\displaystyle -2x=-1}$

${\displaystyle x=1/2.}$

Потім, підставимо це значення для ${\displaystyle x}$ в одне із початкових рівнянь, і отримаємо розв'язок для ${\displaystyle y}$:

${\displaystyle (1/2)^{2}+y^{2}=1}$

${\displaystyle y^{2}=3/4}$

${\displaystyle y={\frac {\pm {\sqrt {3}}}{2}}.}$

Тож, наш перетин містить дві точки:

${\displaystyle \left(1/2,{\frac {+{\sqrt {3}}}{2}}\right)\;\;{\text{i}}\;\;\left(1/2,{\frac {-{\sqrt {3}}}{2}}\right).}$

Метод скорочення: Необхідно додати (або відняти) одне рівняння (із кратним множником) до іншого таким чином, що одна із змінних буде скорочена. Для нашого прикладу, якщо відняти перше рівняння із другого отримаємо ${\displaystyle (x-1)^{2}-x^{2}=0}$. Входження ${\displaystyle y^{2}}$ в першому рівнянні віднімається від ${\displaystyle y^{2}}$ в другому рівнянні, після чого входження змінної ${\displaystyle y}$ в рівнянні не залишається. Змінна ${\displaystyle y}$ була скорочена. Розв'язуємо отримане рівняння відносно ${\displaystyle x}$, так само як у попередньому методі із заміною:

${\displaystyle x^{2}-2x+1+1-x^{2}=1}$

${\displaystyle -2x=-1}$

${\displaystyle x=1/2.}$

Потім підставляємо отримане значення для ${\displaystyle x}$ в одне із початкових рівнянь і розв'язуємо його відносно ${\displaystyle y}$:

${\displaystyle (1/2)^{2}+y^{2}=1}$

${\displaystyle y^{2}=3/4}$

${\displaystyle y={\frac {\pm {\sqrt {3}}}{2}}.}$

Тож наш перетин містить дві точки:

${\displaystyle \left(1/2,{\frac {+{\sqrt {3}}}{2}}\right)\;\;{\text{і}}\;\;\left(1/2,{\frac {-{\sqrt {3}}}{2}}\right).}$

У випадку із конічними перерізами, перетин може містити до 4 точок.

• Обчислювальна геометрія

• Аналітична геометрія // УРЕ
• Аналітична геометрія: підруч. для студ. вищ. техн. навч. закл. / Б. В. Гриньов, І. К. Кириченко. — Х. : Гімназія, 2008. — 340 с.
• Білоусова В. П. та ін. Аналітична геометрія. К., 1957.
• Б. М. Бокало. Навчально-методичний посібник з аналітичної геометрії. — Львів : Видавничий центр ЛНУ ім. І. Франка, 2008. — 262 с. (укр.)
• Лінійна алгебра та аналітична геометрія: навч. посіб. / О. М. Рибицька, Д. М. Білонога, П. І. Каленюк ; М-во освіти і науки, молоді та спорту України, Нац. ун-т «Львів. політехніка». — Л. : Вид-во Львів. політехніки, 2011. — 124 с. : іл. — Бібліогр.: с. 116 (10 назв). — ISBN 978-617-607-142-6 : 1
• Основи аналітичної геометрії та лінійної алгебри: Навч. посіб. для студ. вищ. навч. закл. / Б. В. Ковальчук, Б. М. Тріщ; Львів. нац. ун-т ім. І.Франка. — Л., 2002. — 279 c. — Бібліогр.: 7 назв.
• Привалов И. И. Аналитическая геометрия. Изд. 22. М., 1957. (рос.)
• Делоне Б. Н., Райков Д. А. Аналитическая геометрия, т. 1—2. М.—Л., 1948—49. (рос.)

• АНАЛІТИ́ЧНА ГЕОМЕ́ТРІЯ //ЕСУ