Дужка Кауфмана

Дужка Кауфмана — поліноміальний інваріант обрамленого зачеплення. Хоча він і не є інваріантом вузла або зачеплення (без обрамлення він не є інваріантним відносно руху Рейдемейстера I типу), відповідна «нормалізація» дозволяє перетворити його на варіант знаменитого інваріанта — многочлена Джонса.

Дужку Кауфмана розглянув Луїс Кауфман 1987 року[1].

Визначення

Дужка Кауфмана <L> визначається за довільною (неорієнтованою) діаграмою вузла L за такими правилами:

$\langle O\rangle =1$ , де $O$ — стандартна діаграма тривіального вузла
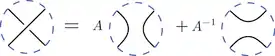
$\langle O\cup L\rangle =(-A^{2}-A^{-2})\langle L\rangle$

Діаграми зачеплень у другому правилі збігаються скрізь, крім невеликого диска — околу перехрестя — де вони влаштовані так, як показано. Третє правило стверджує, що, додаючи до діаграми коло, що не перетинає решти діаграми, ми множимо дужку на $-A^{2}-A^{-2}$ .

Див. також

Многочлен Кауфмана

Примітки

Louis H. Kauffman, State models and the Jones polynomial. Topology 26 (1987), no. 3, 395—407.

Література

В. В. Прасолов, А. Б. Сосинский. Узлы, зацепления, косы и трехмерные многообразия. — М.: МЦНМО, 1997. (рос.)

Посилання

Weisstein, Eric W. Дужка Кауфмана(англ.) на сайті Wolfram MathWorld.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Louis H. Kauffman, State models and the Jones polynomial. Topology 26 (1987), no. 3, 395—407.