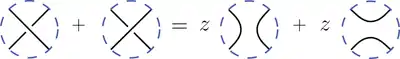Многочлен Кауфмана

Многочлен Кауфмана — многочлен вузла від двох змінних, запропонований Луїсом Кауфманом. Спочатку був визначений на діаграмі зачеплень як:

${\displaystyle F(K)(a,z)=a^{-w(K)}L(K)}$ ,

де ${\displaystyle w(K)}$ — закрученість діаграми зачеплення і ${\displaystyle L(K)}$ — многочлен, визнаячений на діаграмі зачеплення з такими властивостями:

• ${\displaystyle L(O)=1}$ (${\displaystyle O}$ — тривіальний вузол);
• ${\displaystyle L(s_{r})=aL(s),\qquad L(s_{\ell })=a^{-1}L(s)}$ ;
• ${\displaystyle L}$ не змінюється при застосуванні рухів Рейдемейстера типу II і III.

тут ${\displaystyle s}$ — нитка, а ${\displaystyle s_{r}}$ (відповідно, ${\displaystyle s_{\ell }}$) — та ж нитка з додаванням правого (відповідно, лівого) витка (використовуючи рух Рейдемейстера типу I).

Крім того, ${\displaystyle L}$ має задовольняти скейн-співвідношенню Кауфмана:

Малюнки представляють многочлен ${\displaystyle L}$ діаграм, які різні в колі, як показано, але ідентичні зовні^{[уточнити]}

Кауфман показав, що ${\displaystyle L}$ існує і є регулярним ізотопним інваріантом неорієнтованих зачеплень. Звідки випливає, що ${\displaystyle F}$ є обхопним ізотопним інваріантом орієнтованих зачеплень.

Многочлен Джонса — особливий вид многочлена Кауфмана, коли ${\displaystyle L}$ звужується до дужки Кауфмана. Многочлен Кауфмана пов'язаний з калібрувальною теорією Черна — Саймонса для ${\displaystyle \mathrm {SO} (N)}$ так само, як многочлен HOMFLY пов'язаний з калібрувальною теорією Черна — Саймонса для ${\displaystyle \mathrm {SU} (N)}$[1] .