Еквант
Еквант (лат. punctum aequans, від лат.aequo — зрівнюю) — поняття, яке використовували в стародавні та середньовічні вчені в своїх теоріях руху планет, зокрема, Птолемей в геоцентричній системі світу . Згідно з цими теоріями, точка, з якої рух планети виглядає рівномірним, не збігається з геометричним центром траєкторії планети. Ця точка й називається еквантом.
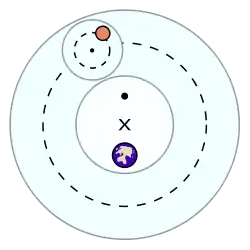
Зодіакальна нерівність у русі Сонця, Місяця та планет

Спостережувальною підставою для введення екванта у стародавні планетні теорії була зодіакальна нерівність в русі небесних тіл. У Сонця та Місяця вона проявляється в нерівномірності їх руху по екліптиці (у випадку Сонця наслідком цього є нерівність пір року). У планет зодіакальна нерівність виявляється в тому, що довжини дуг зворотного руху планети й кутова відстань між ними залежать від того, на який знак зодіаку вони припадають. Ця нерівність найбільш помітна для Марса: в тих знаках зодіаку, коли тривалість зворотних рухів є найменшою, точки на небі, що відповідають середині зворотним рухів (наближено збігаються з протистояннями планет), є рознесеними на найбільшу відстань одна від одної[1].
Відповідно до сучасної теорії руху планет, зодіакальна нерівність викликана тим, що рух планет (в тому числі Землі) є нерівномірним та відбувається не по колу, а по еліпсу (II та I закони Кеплера, відповідно). Однак якщо ексцентриситет орбіти планети дуже малий, то форму її орбіти неможливо відрізнити від окружності, а швидкість руху планети по орбіті практично не відрізняється від розрахованої за допомогою теорії екванту[2].
Птолемеєва теорія бісекції ексцентриситету
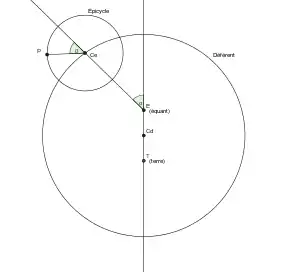
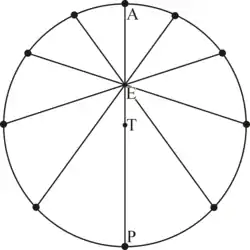
Астрономи давнини та середньовіччя виходили з принципу, що траєкторії планет повинні бути суперпозицією рівномірних кругових рухів. Для пояснення зворотних рухів планет вони припускали, що кожна планета рухається по малому колу (епіциклу), центр якого (середня планета), у свою чергу, переміщується навколо Землі по великому колу (деферента). Необхідність пояснення зодіакальної нерівності змусила Клавдія Птолемея (II століття н. е.) припустити, що рух середньої планети виглядає рівномірним при спостереженні не з центру деферента, а з певної точки, яка і називається еквантом, або зрівнювальною точкою. При цьому Земля також перебуває не в центрі деферента, а зміщена в бік симетрично до точки екванта відносно центру деферента (див. малюнок). Ця модель називається теорією бісекції ексцентриситету, оскільки в ній відрізок, що з'єднує Землю та еквант, ділиться центром деферента на дві рівні частини. У теорії Птолемея кутова швидкість центру епіциклу щодо екванта незмінна, а при спостереженні з центру деферента кутова швидкість центру епіциклу при русі планети змінюється. Не залишається незмінною й лінійна швидкість середньої планети: чим ближче до Землі, тим вона більша. Відстань і лінійна швидкість середньої планети в апогеї та перигеї пов'язані між собою як , де індекси та належать до апогею та перигею, відповідно.
Птолемей визначив параметри теорії екванта для кожної з планет виходячи з астрономічних спостережень. Вмілий підбір положення екванта дозволив Птолемею достатньо точно змоделювати видимий нерівномірний рух планет.
Більшість істориків астрономії приписують авторство теорії бісекції ексцентриситету і саме введення поняття екванта саме Птолемею[3]. Останнім часом, однак з'явилися підстави вважати, що основи цієї теорії були закладені давньогрецькими астрономами попереднього періоду (див. нижче).
Теорія екванта у середньовічних мусульманських астрономів
Концепція екванта була вдалим, хоча й штучним, математичним засобом, однак вона різко дисонувала із загальною ідеологією античної астрономії, згідно з якою всі рухи по небесній сфері є рівномірними та круговими. У середні віки відмічали ще одну складність, чисто фізичного характеру: рух середньої планети по деференту уявлявся як обертання деякої матеріальної сфери (в яку була вбудована ще одна, мала сфера, обертання якої було рухом планети по епіциклу). Однак, як відзначали багато середньовічних ісламських астрономів (починаючи з ібн ал-Хайсама, XI століття), абсолютно неможливо уявити собі обертання твердого тіла навколо осі, що проходить через її центр, щоб швидкість обертання була незмінною відносно деякої точки за межами осі обертання.
З метою подолання цього утруднення астрономи країн ісламу розробили низку моделей руху планет, альтернативних птолемеївській (хоча вони також були геоцентричними). Перші з них були розроблені в другій половині XIII століття астрономами знаменитої Марагінської обсерваторії, завдяки чому і всі спроби побудувати нептолемеївські планетні теорії іноді називають Марагінською революцією. Серед цих астрономів були організатор та перший директор цієї обсерваторії Насир ад-Дін ат-Тусі, його учень Кутб ад-Дін аш-Ширазі, головний конструктор приладів для цієї обсерваторії Муаййад ад-Дін аль-Урді та інші. Цю діяльність продовжили східні астрономи пізнішого часу: Мухаммад ібн аш-Шатир (Сирія, XIV ст.), Мухаммад ал-Хафра (Іран, XVI ст.) та ін.
Згідно з цими теоріями, рух відносно точки, відповідній до птолемеївського екванта, виглядав рівномірним, але замість нерівномірного руху по одному колу (як це відбувалось у Птолемея) середня планета рухалася по комбінації рівномірних рухів по декількох колах.[4] Оскільки вся ці рухи були рівномірними, вони моделювались обертанням твердих сфер, що усувало розбіжність математичної теорії планет з її фізичним фундаментом. З іншого боку, ці теорії зберігали точність теорії Птолемея, оскільки при спостереженні з екванта рух, як і раніше, виглядав рівномірним, а результуюча просторова траєкторія середньої планети практично не відрізнялася від кола.
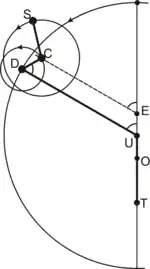
Наприклад, в теорії ал-Урді (яку визнав також аш-Ширазі) центром деферента планети є точка U, розташована посередині між птолемеївським центром деферента O і еквантом E. По деференту рівномірно рухається точка D, що є центром допоміжного епіциклу, по якому рівномірно рухається точка C, що є центром основного епіциклу планети, тобто середньою планетою. Сама планета S рухається по другому, основному епіциклу. Швидкості руху по деференту та малому епіциклу підібрані таким чином, щоб чотирикутник UECD залишався рівнобедреною трапецією. Оскільки центр малого епіциклу D рухається по деференту рівномірно, то кут між відрізком CE (з'єднує середню планету та еквант) і лінією апсид ТО також змінюється рівномірно, тобто рух середньої планети з точки екванта виглядає рівномірним. Траєкторія середньої планети C злегка відрізняється від кола, але ця відмінність настільки мала, що відмінність положення планети в теорії ал-Урді від теорії Птолемея жодним чином не можна виявити неозброєним оком.
Теорія екванта в астрономів Нового часу
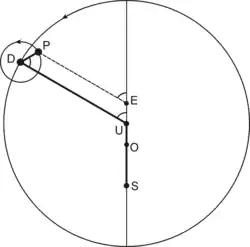
Як вважають деякі історики науки, саме бажання уникнути нерівномірності в русі планет, пов'язаної з еквантом, спонукало Миколу Коперника приступити до розробки геліоцентричної системи світу[5]. Для того, щоб пояснити зодіакальну нерівність він застосовував ті самі геометричні побудови, що й середньовічні ісламські астрономи[6]. Так, його теорія руху зовнішніх планет (викладена в книзі Про обертання небесних сфер) ідентична теорії руху середньої планети в моделі ал-Урді, з тією відмінністю, що рух відбувається навколо Сонця, а не Землі. Не виключено, що Коперник знав про ці моделі, хоча можливі шляхи проникнення цієї інформації в Європу поки невідомі[7].
Вчені XVI століття вважали головним досягненням Коперника не геліоцентричну систему світу, а суворе дотримання принципу рівномірних кругових рухів[8]. Тим не менш, були й інші спроби пояснення зодіакального нерівності. Так, астрономи, які працювали в обсерваторії Тихо Браге (особливо Лонгомонтан) відзначили, що високої точності при визначенні довготи планети можна досягти, якщо припустити, що відстані від землі і від екванта до центру деферанта не рівні одна одній[9], а відносяться як 5 до 3.
Подальший розвиток планетної теорії пов'язаний з ім'ям Йоганна Кеплера. На ранніх стадіях роботи над обробкою спостережень Тихо Браге він розглядав різні варіанти теорії екванта (бисекцію ексцентриситету, теорію Браге-Лонгомонтана), але не для руху центрів планетних епіциклів навколо Землі, а для руху планет та Землі навколо Сонця. Однак у кінцевому підсумку він прийшов до своїх знаменитих законів руху планет, тим самим остаточно вирішивши проблему зодіакальної нерівності. Втім, не всі астрономи одразу дізнались про досягнення Кеплера, і багато з них як і раніше розглядали теорію екванта. Це стосується, наприклад, Ісаака Ньютона на ранніх стадіях його роботи над планетною теорією[10].
Теорія руху планет у середньовічних індійських астрономів і генезис теорії екванта
Основна лінія розвитку астрономії проходить від стародавніх греків через середньовічних астрономів ісламу до європейських астрономів Нового часу. Паралельно до неї відбувався розвиток теорії руху планет в середньовічній Індії. Найвизначнішим з індійських астрономів був Аріабхата (V століття н. е.). Для того, щоб вичислити розташування планет на небі він використовував своєрідну модифікацію теорії епіциклів. Як уперше показав Бартель ван дер Варден, ця теорія математично еквівалентна до птолемеївської теорії бісекції ексцентриситету. Ця точка зору отримала підтримку в працях низки сучасних істориків науки.[11] З іншого боку, щоб змоделювати рухи Сонця та Місяця індійські астрономи використовували теорію, еквівалентну до теорії концентричного екванта, в якій Земля розташована в геометричному центрі орбіти світила, але швидкість руху світила змінюється таким чином, що його рух виглядає рівномірним при спостереженні з точки, зміщеної відносно його центру, тобто екванта[12]. Як вважають більшість сучасних дослідників, індійська астрономія безпосередньо базується на грецькій астрономії доптолемеївського (і навіть догіппархівського) періоду[13], тому виглядає обґрунтованим припущення, що ці теорії в кінцевому підсумку базуються на теоріях грецьких астрономів, які не дійшли до нас[14]. Якщо це так, то видається цілком природною точка зору ван дер Вардена, що поняття про еквант та теорія бісекції ексцентриситету є здобутком не Птолемея, а його попередників[15].
Примітки
- Evans 1984, 1998.
- Brenke 1936, Evans 1988, Ньютон 1985.
- Різні припущення щодо того, як міг прийти Птолемей до цієї теорії, викладені в працях Evans (1984, 1998), Swerdlow (2004), Джонс (2004), Duke (2005b).
- Рожанская 1976 (с. 268 — 286); Kennedy 1966; Saliba 1991, 1996.
- Swerdlow 1973.
- Hartner 1973, Swerdlow 1973, Guessoum 2008.
- Можливо, проміжною ланкою були вчені Візантії, серед яких були ті, що вивчали астрономію в ісламських країнах. Див. Ragep 2007, а також G. Saliba, Arabic/Islamic Science And Renaissance Science in Italy.
- Westman 1975.
- Evans 1998, pp. 431 — 433.
- Whiteside 1964.
- Thurston 1992, Duke 2005a.
- Pingree 1974, Duke 2008.
- Нейгебауер 1968, с. 165 — 174; Pingree 1971, 1976; van der Waerden 1987; Duke 2005a.
- Duke 2008.
- У своїй роботі Rawlins (1987) припускає, що справжніми авторами теорії экванта були давньогрецькі прихильники геліоцентричної системи світу.
Див. також
Література
- Еремеева А. И., Цицин Ф. А. История астрономии. — М. : Изд-во МГУ, 1989.
- Ідельсон Н. І. Етюди з історії небесної механіки. — М. : Наука, 1975. (рос.)
- Нейгебауер O. Точні науки в давнину. — М. : Наука, 1968. (рос.)
- Ньютон Р. Злочин Клавдія Птолемея. — М. : Наука, 1985. (рос.)
- Паннекук А. Історія астрономії. — М. : Наука, 1966. (рос.)
- Рожанская М. М. Механика на средневековом Востоке. — Москва : Наука, 1976.
- Рожанский И. Д. История естествознания в эпоху эллинизма и Римской империи. — М. : Наука, 1988.
- W. C. Brenke, «An angle connected with the mean place in the ellipse», Popular Astronomy, 44, p.76-77, 1936. Online
- Dreyer J. L. E. History of the planetary systems from Thales to Kepler. — Cambridge University Press, 1906.
- D. Duke, «The Equant in India: The Mathematical Basis of Ancient Indian Planetary Models», Archive for History of Exact Sciences, V. 59, No 6, 2005a.
- D. Duke, «Comment on the Origin of the Equant papers by Evans, Swerdlow, and Джонс», Journal for the History of Astronomy", V. 36, Part 1, No. 12, p. 1-6, 2005b. Online
- D. Duke, «An Interesting Property of the Equant», DIO, V. 15, pp. 24-37, 2008.
- J. Evans, «On the function and the probable origin of Ptolemy's equant», American Journal of Physics, V. 52, Issue 12, pp. 1080 — 1089, 1984.
- J. Evans, «The division of the Martian eccentricity from Hipparchos to Kepler: A history of the approximations to Kepler motion», American Journal of Physics, V. 56, Issue 11, pp. 1009 — 1024, 1988.
- Evans J. The History and Practice of Ancient Astronomy. — New York : Oxford University Press, 1998.
- Guessoum N. Copernicus and Ibn Al-Shatir: does the Copernican revolution have Islamic roots? // The Observatory. — 2008. — Т. 128. — С. 231 — 239.
- Hartner W. Copernicus, the Man, the Work, and its History // Proceedings of the American Philosophical Society. — 1973. — Т. 117. — С. 413 — 422.
- A. Джонс, «A Route to the ancient discovery of nonumiform planetary motion», Journal for the history of astronomy, V. 35, p. 375 — 386, 2004. Online
- Kennedy E. S. Late Medieval Planetary Theory // Isis. — 1966. — Т. 57. — С. 365 — 378.
- Koyre A. The Astronomical Revolution. — New York : Dover, 1973.
- Linton C. M. From Eudoxus to Einstein. — Cambridge University Press, 2004.
- Pingree D. On the Greek Origin of the Indian Planetary Model Employing a Double Epicycle // Journal of the History of Astronomy. — 1971. — Т. 2. — С. 80 — 85.
- Pingree D. Concentric with Equant // Archives Internationales d'Histoire des Sciences. — 1974. — Т. 24. — С. 26 — 28.
- Pingree D. The Recovery of Early Greek Astronomy from India // Journal of the History of Astronomy. — 1976. — Т. 7. — С. 109 — 123.
- Ragep F. J. The Two Versions of the Tusi Couple // in: From Deferent to Equant. A Volume of Studies on the History of Science in the Ancient and Medieval Near East in Honor of E.S. Kennedy (Annals of the New York Academy of Sciences). — New York, 1987. — Т. 500. — С. 329 — 356.
- Ragep F. J. Copernicus and his Islamic Predecessors: Some historical Remarks // History of Science. — 2007. — Т. 45. — С. 65 — 81.
- Rawlins D. Ancient Heliocentrists, Ptolemy, and the equant // American Journal of Physics. — 1987. — Т. 55. — С. 235-9.
- Saliba G. The Astronomical Tradition of Maragha: A Historical Survey and Prospects for Future Research // Arabic Sciences and Philosophy. — 1991. — Т. 1. — С. 67 — 99.
- Saliba G. Arabic Planetary Theories after the Eleventh Century AD // in: Encyclopedia of the History of Arabic Science. — London : Routledge, 1996. — С. 58 — 127.
- N. M. Swerdlow, «The Derivation and First Draft of Copernicus's Planetary Theory: A Translation of the Commentariolus with Commentary», Proceedings of the American Philosophical Society, V. 117, pp. 423 — 512, 1973.
- N. M. Swerdlow, «The empirical foundations of Ptolemy's planetary theory», Journal for the History of Astronomy, V. 35, Part 3, No. 120, p. 249 — 271, 2004. Online
- H. Thurston, «Greek and Indian planetary longitudes», Archive for History of Exact Sciences, V. 44, No 3, p. 191 — 195, 1992.
- Thurston H. Early astronomy. — New York : Springer-Verlag, 1994.
- Van der Waerden B. L. The heliocentric system in Greek, Persian and Hindu astronomy // In: From deferent to equant: A Volume of Studies in the History of Science in the Ancient and Medieval Near East in Honor of E.S. Kennedy. — Annals of the New York Academy of Sciences, 1987, June. — Т. 500. — С. 525 — 545.
- Westman R. S. The Melanchthon Circle, Rheticus, and the Wittenberg Interpretation of the Copernican Theory // Isis. — 1975. — Т. 66, No. 2. — С. 164 — 193.
- D. T. Whiteside, «Newton's Early Thoughts on Planetary Motion: A Fresh Look», The British Journal for the History of Science, Vol. 2, No. 2, pp. 117 — 137, 1964.