Функція розподілу ймовірностей

Зверху вниз:
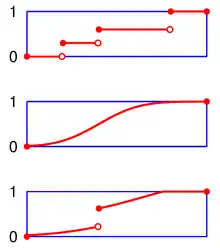
функція розподілу для дискретного розподілу ймовірностей, для неперервного розподілу та для розподілу, що містить дискретну та неперервну частини.

Якщо ${\displaystyle \xi }$ є дискретною випадковою величиною, що набуває значень ${\displaystyle x_{1},x_{2},...}$ із ймовірністю ${\displaystyle p_{i}=P(x_{i})}$, то функція розподілу для ${\displaystyle \xi }$ буде розривною в точках ${\displaystyle x_{i}}$ і неперервною поміж ними:

${\displaystyle F(x)=\operatorname {P} (\xi \leq x)=\sum _{x_{i}\leq x}\operatorname {P} (\xi =x_{i})=\sum _{x_{i}\leq x}p(x_{i})}$

Легко бачити, що:

• ${\displaystyle F_{\xi }(x)\,}$ не спадає на всій числовій прямій.
• ${\displaystyle F_{\xi }(x)\,}$ неперервна справа.
• ${\displaystyle \lim \limits _{x\to -\infty }F_{\xi }(x)=0\,}$.
• ${\displaystyle \lim \limits _{x\to \infty }F_{\xi }(x)=1\,}$.

З властивостей ймовірності випливає, що для всіх ${\displaystyle x\in \mathbb {R} }$ і для всіх ${\displaystyle a,b\in \mathbb {R} }$, таких що ${\displaystyle a<b}$ матимуть місце співвідношення:

• ${\displaystyle P(\xi >x)=1-F_{\xi }(x)\,}$;
• ${\displaystyle P(\xi <x)=F_{\xi }(x-)\,}$;
• ${\displaystyle P(\xi \geq x)=1-F_{\xi }(x-)\,}$;
• ${\displaystyle P(\xi =x)=F_{\xi }(x)-F_{\xi }(x-)\,}$;
• ${\displaystyle P(a<\xi \leq b)=F_{\xi }(b)-F_{\xi }(a)\,}$;
• ${\displaystyle P(a\leq \xi \leq b)=F_{\xi }(b)-F_{\xi }(a-)\,}$;
• ${\displaystyle P(a<\xi <b)=F_{\xi }(b-)-F_{\xi }(a)\,}$;
• ${\displaystyle P(a\leq \xi <b)=F_{\xi }(b-)-F_{\xi }(a-)\,}$.

• Скороход А.В. (1990). Лекції з теорії випадкових процесів (українська). Київ: Либідь. ISBN 5-11-001701-8.

• Функція щільності
• Нерівність Чебишева
• Емпірична функція розподілу
• Статистика Петуніна
• Функція Салема