Завісні втрати
Завісні втрати (англ. hinge loss) у машинному навчанні — це функція втрат, яка використовується для навчання класифікаторів.[1] Завісні втрати використовують для максимальної розділової класифікації, здебільшого для опорних векторних машин (ОВМ). Для поміченого виходу t = ±1 та оцінки класифікатора y, завісна втрата передбачення y визначається як
Варто зауважити, що тут y є «сирим» значенням функції прийняття рішення у класифікаторі, а не міткою класу. Наприклад, в лінійних ОВМ , де є параметрами гіперплощини та — точка, яку потрібно класифікувати.
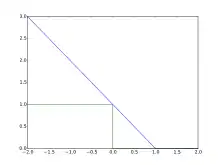
Зрозуміло, що коли t та y мають однаковий знак (що означає, що y вказує на правильний клас) та , тоді завісні втрати , а коли вони мають різні знаки, то зростає лінійно від y (одностороння помилка). На рисунку пояснюється, чому завісні втрати дають кращу оцінку втрат ніж функція нуль-один.
Узагальнення
Хоч є поширеною практикою узагальнення бінарних ОВМ на багатокласову ОВМ у режимі один з усіх або один в один,[2] також можливе узагальнення з використанням завісної функції. Було запропоновано декілька різних багатокласових завісних втрат.[3] Наприклад, Крамер та Сінгер[4] дали таке визначення у випадку лінійного класифікатора:[5]
Тут — мітка цілі, та — параметри моделі.
Вестон і Воткінс дали подібне визначення, але з сумою замість максимуму:[6][3]
При структуровому передбачуванні завісні втрати можуть бути поширені на структуровані вихідні простори. Структурова опорно-векторна машина з масштабуванням розділення використовує наступний варіант, де w позначає параметри ОВМ, y — передбачення ОВМ, φ додає функцію ознак та Δ є відстанню Геммінга:
Оптимізація
Завісні втрати є опуклою функцією, отже, опуклі оптимізатори, що використовуються у машинному навчанні, можуть працювати з ними. Це не диференційовна функція, проте вона має субградієнт відносно параметрів моделі w лінійної ОВМ з функцією оцінки , який буде
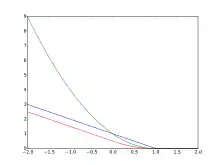
Однак, оскільки похідна завісних втрат при невизначена, то гладкий варіант, запропонований Ренні та Сребро, є більш бажаним для оптимізації[7]
або квадратично гладкий
запропонований Чангом.[8] Модифікований варіант втрат Губера є спеціальним випадком цієї функції втрат з , зокрема, .
Примітки
- Rosasco, L.; De Vito, E. D.; Caponnetto, A.; Piana, M.; Verri, A. (2004). Are Loss Functions All the Same?. Neural Computation 16 (5): 1063–1076. PMID 15070510. doi:10.1162/089976604773135104.
- Duan, K. B.; Keerthi, S. S. (2005). Which Is the Best Multiclass SVM Method? An Empirical Study. Multiple Classifier Systems. LNCS 3541. с. 278–285. ISBN 978-3-540-26306-7. doi:10.1007/11494683_28.
- Doğan, Ürün; Glasmachers, Tobias; Igel, Christian (2016). A Unified View on Multi-class Support Vector Classification. J. Machine Learning Research 17: 1–32.
- Crammer, Koby; Singer, Yoram (2001). On the algorithmic implementation of multiclass kernel-based vector machines. J. Machine Learning Research 2: 265–292.
- Moore, Robert C.; DeNero, John (2011). L1 and L2 regularization for multiclass hinge loss models. Proc. Symp. on Machine Learning in Speech and Language Processing.
- Weston, Jason; Watkins, Chris (1999). Support Vector Machines for Multi-Class Pattern Recognition. European Symposium on Artificial Neural Networks.
- Rennie, Jason D. M.; Srebro, Nathan (2005). Loss Functions for Preference Levels: Regression with Discrete Ordered Labels Proc. IJCAI Multidisciplinary Workshop on Advances in Preference Handling.
- Zhang, Tong (2004). Solving large scale linear prediction problems using stochastic gradient descent algorithms ICML.