Задача Штейнера
Задача Штейнера (Задача дерева Штейнера) полягає у пошуку мінімального дерева Штейнера — найкоротшої мережі, що з'єднує заданий скінченний набір точок площини. Свою назву отримала на честь Якоба Штейнера (1796–1863).
Історія
Історія цієї задачі сягає часу П'єра Ферма (1601–1665), який, після викладу свого методу дослідження мінімумів та максимумів, написав [1]:
Qui hanc methodum non probaverit, ei proponitur: Datis tribus punctis, quartum reperire, a quo si ducantur tres rectae ad data puncta, summa trium harum rectarum sit minima quantitas.
Той же, хто цей метод не оцінив, нехай він вирішить [наступну задачу]: для заданих трьох точок знайти таку четверту, що якщо з неї провести три відрізки в дані точки, то сума цих трьох відрізків дасть найменшу величину.
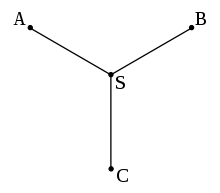
Ця задача була частково розв'язана Еванджелістою Торрічеллі[2][3] (1608–1647) і Бонавентурою Кавальєрі[4] (1598–1647), учнями Бенедетто Кастеллі (1577–1644), потім знайдена ними конструкція була модифікована Томасом Сімпсоном[5] (1710–1761) і остаточно уточнена Ф. Гайненом[6] і Жозефом Бертраном (1822–1900). У результаті було отримано геометричну побудову точки S, що називається точкою Ферма (іноді точкою Торрічеллі), яка для трьох заданих точок A, B і C дає мінімально можливу суму довжин відрізків AS, BS, CS.
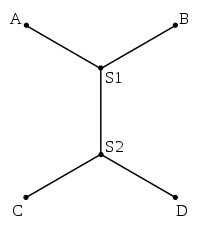
1934 року В. Ярнік і O. Кесслер[7] сформулювали узагальнення задачі Ферма, замінивши три точки на довільне скінченне число. Їх задача полягає в описі зв'язаних плоских графів найменшої довжини, що проходять через дану скінченну множину точок площини.
1941 року вийшла монографія Ріхарда Куранта і Герберта Роббінса «Що таке математика?»[8], в якій автори написали наступне:
| Дуже проста та разом з тим повчальна проблема була вивчена на початку минулого століття знаменитим берлінським геометром Якобом Штейнером. Потрібно з'єднати три села , , системою доріг таким чином, щоб їх загальна довжина була мінімальною.Було б природно узагальнити цю проблему на випадок заданих точок таким чином: потрібно знайти в площині таку точку , щоб сума відстаней (де позначає відстань ) ставала мінімальною... . Ця узагальнена проблема, також вивчена Штейнером, не веде до цікавих результатів. У цьому випадку ми маємо справу з поверхневим узагальненням, подібних якому чимало зустрічається в математичній літературі. Щоб отримати дійсно гідне уваги узагальнення проблеми Штейнера, доводиться відмовитися від пошуків однієї-єдиної точки . Замість того поставимо завданням побудувати «вуличну мережу» або «мережу доріг між даними селами», що має мінімальну загальну довжину[8]. |
Ця книга завоювала заслужену популярність, внаслідок чого і задачу Ферма, і задачу Ярніка-Кесслера зараз прийнято називати проблемою Штейнера.
Алгоритм розв'язування
Ефективного (складність виражається функцією, обмеженою зверху деяким поліномом від параметра завдання, в даному випадку число вершин графу) алгоритму, що дає точне рішення проблеми Штейнера, не існує. Наближене рішення дає ефективний алгоритм Крускала[9].
Основні визначення
Наведемо кілька сучасних формулювань проблеми Штейнера. Як осяжний простір замість евклідової площини розглянемо довільний метричний простір.
Мінімальні дерева Штейнера
Нехай — метричний простір і — граф на X, тобто, . Для кожного такого графу визначені довжини його ребер , як відстані між їх вершинами, а також довжина самого графу , як сума довжин всіх його ребер.
Якщо — скінченна підмножина , а — зв'язний граф на , для якого , то називається графом, що з'єднує . При цьому граф , що з'єднує , мінімально можливої довжини є деревом, яке називається мінімальним деревом Штейнера на . Саме вивченню таких дерев і присвячена одна з версій проблеми Штейнера.
Зазначимо, що мінімальні дерева Штейнера існують не завжди. Проте, точна нижня грань величин по всім зв'язним графам, що з'єднує , завжди існує, називається довжиною мінімального дерева Штейнера на та позначається через .
Приклади
Якщо — стандартна евклідова площина, тобто відстань породжується нормою , то отримуємо класичну проблему Штейнера, сформульовану Ярніком та Кесслером (див. вище).
Якщо — Манхеттенська відстань, тобто відстань породжується нормою , то отримуємо прямокутну проблему Штейнера, одним з додатків якої є проектування розводок мікросхем. Більш сучасні розводки моделюються метрикою, породженою λ-нормою (одиничне коло — правильний 2λ-кутник; в цих термінах манхеттенська норма є 2-нормою).
Якщо як береться сфера (яка приблизно моделює поверхню Землі), а за — довжина найкоротшої з двох дуг великого кола, яка висікається з сфери площиною, що проходить через , та центр сфери, то виходить різновид транспортної задачі: потрібно з'єднати заданий набір пунктів (міст, підприємств, абонентів і т. д.) найкоротшою комунікаційною мережею (доріг, трубопроводів, телефонних ліній і т. д.), мінімізувавши витрати на будівництво (передбачається, що витрати пропорційні довжині мережі).
Якщо як береться множина всіх слів над деяким алфавітом, а як — відстань Левенштейна, то виходить варіант проблеми Штейнера, який широко використовується в біоінформатиці, зокрема, для побудови еволюційного дерева.
Якщо як береться множина вершин зв'язного графу , а як — функція відстані, породжена деякою ваговою функцією , то виходить проблема Штейнера у графах.
Мінімальні параметричні мережі
Нехай — деяка підмножина множини вершин графу , що містить всі вершини ступеня 1 і 2. Пара називається графом з кордоном . Якщо — зв'язний граф, і — деяке відображення в метричний простір , то кожне відображення , обмеження якого на збігається з , називається мережею типу з кордоном в метричному просторі . Обмеження мережі на вершини та ребра графу називаються відповідно вершинами і ребрами цієї мережі. Довжиною ребра мережі називається величина , а довжиною мережі — сума довжин всіх її ребер.
Позначимо через безліч всіх мереж типу з кордоном . Мережа з , що має найменшу можливу довжину, називається мінімальною параметричною мережею типу з кордоном .
Зазначимо, що, як і у випадку мінімальних дерев Штейнера, мінімальна параметрична мережа існує не завжди. Проте, точна нижня грань величин по всіх мережах з , завжди існує, називається довжиною мінімальної параметричної мережі і позначається через .
Якщо — скінченна підмножина , а відображає на всі , тобто , то говорять, що мережа з'єднує . Легко побачити, що по всім , для яких . Таким чином, загальна задача Штейнера зводиться до вивчення мінімальних параметричних мереж та вибору з них найкоротших.
Одновимірні мінімальні заповнення в сенсі Громова
Це природне узагальнення проблеми Штейнера було запропоновано А. О. Івановим і А. А. Тужиліним.[10] Нехай — довільна скінченна множина і — деякий зв'язний граф. Будемо говорити, що з'єднує , якщо . Нехай тепер — скінченний псевдометричний простір (де, на відміну від метричного простору, відстані між різними точками можуть бути рівні нулю), — зв'язний граф, що з'єднує , і — деяке відображення в невід'ємні дійсні числа, як правило зване ваговою функцією і породжує зважений граф . Функція задає на псевдометріку , а саме, відстанню між вершинами графу назвемо найменшу з ваг шляхів, що з'єднують ці вершини. Якщо для будь-яких точок та з виконується , то зважений граф називається заповненням простору , а граф — типом цього заповнення . Число , рівне по всіх заповненнях простору , назвемо вагою мінімального заповнення , а заповнення , для якого , — мінімальним заповненням . Основне завдання — навчитися обчислювати і описувати мінімальні заповнення.
Примітки
- Fermat P. de (1643). У Ed. H.Tannery. "Oeuvres" 1. Paris 1891, Supplement: Paris 1922. с. 153.
- G. Loria, G. Vassura (1919). Opere de Evangelista Torriceli 1. с. 79–97.
- J. Krarup, S. Vajda (1997). On Torricelli's geometrical solution to a problem of Fermat. IMA J. Math. Appl. Bus. Indust. 8 (3): 215–224. doi:10.1093/imaman/8.3.215.
- B. Cavalieri (1647). Excercitationes Geometricae.
- T. Simpson (1750). "The Doctrine and Application of Fluxions".
- F. Heinen (1834). Über Systeme von Kräften. Gymnasium zu Cleve (Essen).
- V. Jarník, O. Kössler (1934). O minimálních grafech obsahujících n daných bodu. Ĉas, Pêstování Mat. (Essen) 63: 223–235.[недоступне посилання з липня 2019]
- R. Courant, H. Robbins (1941). What Is Mathematics?. Oxford University Press.
- Белоусов А. И., Ткачев С. Б. {{{Заголовок}}}. — ISBN 5-7038-2886-4.
- A. O. Ivanov, A. A. Tuzhilin. One-dimensional Gromov minimal filling.
Література
- А. О. Іванов, А. А. Тужилін. Теорія екстремальних мереж. — Москва-Іжевськ : Інститут комп'ютерних досліджень, 2003. — ISBN 5-93972-292-X.
- А. О. Іванов, А. А. Тужилін. Задача Штейнера на площині або плоскі мінімальні мережі // матем. сб.. — 1991. — Т. 182, № 12. — С. 1813-1844.
- Weisstein, Eric W. Steiner Tree(англ.) на сайті Wolfram MathWorld.
