Задача про кліку
Задача про кліку відноситься до класу NP-повних задач в області теорії графів. Вперше вона була сформульована у 1972 році Річардом Карпом.[1]
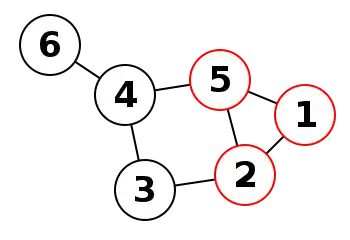
Клікою в неорієнтованому графі називається підмножина вершин, кожні дві з яких з'єднані ребром графу. Іншими словами, це повний підграф первісного графу. Розмір кліки визначається як число вершин в ній. Задача про кліку існує у двох варіантах: у задачі розпізнавання потрібно визначити, чи існує в заданому графі G кліка розміру k, тоді як в обчислювальному варіанті потрібно знайти в заданому графі G кліку максимального розміру або всі максимальні кліки (такі, що не можна збільшити).
Історія
Хоча повні підграфи довгий час вивчалися в математиці[2], термін «кліка» і задача алгоритмічно оголошеного кліка обидва походять із соціальних наук, де повні підграфи використовувались як модель соціальних кліків, груп людей, які всі знають один одного. Термінологія «кліка» походить від Люса та Перрі (1949), та перший алгоритм рішення задачі про кліку винайшли Харарі та Росс (1957), для соціологічних досліджень.
Після роботи Харарі і Росса, багато інших авторів розробили алгоритми для розв'язання різних версій задачі про кліку. У 1970-х, дослідники почали вивчати ці алгоритми з точки зору найгіршого аналізу; див., наприклад, Тарьян та Трояновськи (1977), перші роботи про вирішення найгіршого максимального кліку. Крім того, у 1970-х роках, починаючи з роботи Кука (1971) і Карпа (1972), дослідники почали знаходити математичне обґрунтування для сприйманої складності кліку проблеми в теорії NP-повноти і пов'язаних незговірливих результатів. У 1990-ті роки, був написаний цикл робіт, починаючи з Фейга і співавт. (1991) і повідомив у той час пресі[3] про те, що неможливо вирішити цю задачу максимально точно та ефективно.
NP-Повнота
NP-повнота задачі про кліку випливає з NP-повноти задача про незалежну множину (вершин). Легко показати, що необхідною і достатньою умовою для існування кліки розміру k є наявність незалежної множини розміру не менше k в доповненні графу. Це очевидно, оскільки повнота підграфу означає, що його доповнення не містить жодного ребра.
Інший доказ NP-повноти можна знайти в книзі «Алгоритми: побудова й аналіз».[4]
Алгоритми
Як і для інших NP-повних задач, ефективного алгоритму для пошуку кліки заданого розміру на даний момент не знайдено. Повний перебір всіх можливих підграфів розміру k з перевіркою того, чи є хоча б один з них повним, — неефективний, оскільки повне число таких підграфів в графі з v вершинами збігається біноміальним коефіцієнтом
Інший алгоритм працює так: дві кліки розміру n і m «склеюються» у велику кліку розміру (n + m), причому клікою розміру 1 покладається окрема вершина графу. Алгоритм завершується, як тільки жодного злиття більше здійснити не можна. Час роботи даного алгоритму є лінійним, проте він є евристичним, оскільки не завжди призводить до знаходження кліки максимального розміру. Як приклад невдалого завершення можна навести випадок, коли вершини, що належать максимальній кліці, виявляються розділені й перебувають у кліках меншого розміру, причому останні вже не можуть бути «склеєними» між собою.
Див. також
- Алгоритм Брона-Кербоша — швидкий пошук клік
- Соціальний граф
- Словник термінів теорії графів
Примітки
- Karp, Richard (1972). Reducibility Among Combinatorial Problems. Proceedings of a Symposium on the Complexity of Computer Computations. Plenum Press.
- Complete subgraphs make an early appearance in the mathematical literature in the graph-theoretic reformulation of Ramsey theory by Erdős та Szekeres, (1935).
- Kolata, Gina (26 червня 1990). In a Frenzy, Math Enters Age of Electronic Mail. New York Times..
- Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4
Література
- Cook, Stephen A. (1971). The Complexity of Theorem-Proving Procedures. Proceedings of the Third Annual ACM Symposium on Theory of Computing. Shaker Heights, Ohio. с. 151–158. Архів оригіналу за 3 травня 2006. Процитовано 11 червня 2007.
- Garey, Michael R.; Johnson, David S. (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman. ISBN 0-7167-1045-5. A1.2: GT19, pg.194.
- Cook, S. A. (1971). The complexity of theorem-proving procedures. Proc. 3rd ACM Symposium on Theory of Computing. с. 151–158. doi:10.1145/800157.805047..
- Downey, R. G.; Fellows, M. R. (1995). Fixed-parameter tractability and completeness. II. On completeness for W[1]. Theoretical Computer Science 141 (1–2): 109–131. doi:10.1016/0304-3975(94)00097-3.
- Downey, R. G.; Fellows, M. R. (1999). Parameterized complexity. Springer-Verlag. ISBN 0-387-94883-X..
- Eisenbrand, F.; Grandoni, F. (2004). On the complexity of fixed parameter clique and dominating set. Theoretical Computer Science 326 (1–3): 57–67. doi:10.1016/j.tcs.2004.05.009.
- Eppstein, David; Löffler, Maarten; Strash, Darren (2010). Listing All Maximal Cliques in Sparse Graphs in Near-Optimal Time. У Cheong, Otfried; Chwa, Kyung-Yong; Park, Kunsoo. 21st International Symposium on Algorithms and Computation (ISAAC 2010), Jeju, Korea. Lecture Notes in Computer Science 6506. Springer-Verlag. с. 403–414. ISBN 978-3-642-17516-9. arXiv:1006.5440. doi:10.1007/978-3-642-17517-6_36.
- Eppstein, David; Strash, Darren (2011). Listing all maximal cliques in large sparse real-world graphs. 10th International Symposium on Experimental Algorithms. arXiv:1103.0318..
- Erdős, Paul; Szekeres, George (1935). A combinatorial problem in geometry. Compositio Mathematica 2: 463–470..