Соціальний граф
Соціальний граф (англ. Social graph) — це граф, вузли якого представлені соціальними об'єктами, такими як профілі користувача з різними атрибутами (наприклад: ім'я, день народження, рідне місто, тощо), співтовариства, медіа-контент[1], тощо, а ребра — соціальними зв'язками між ними[2][3].
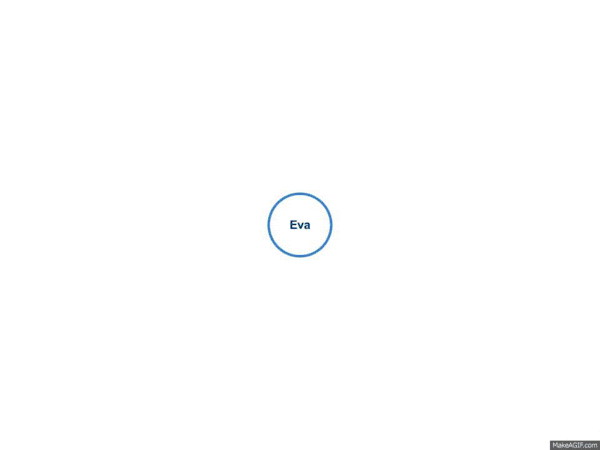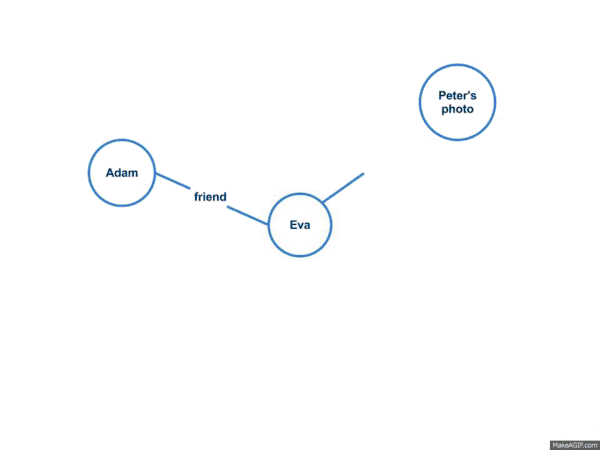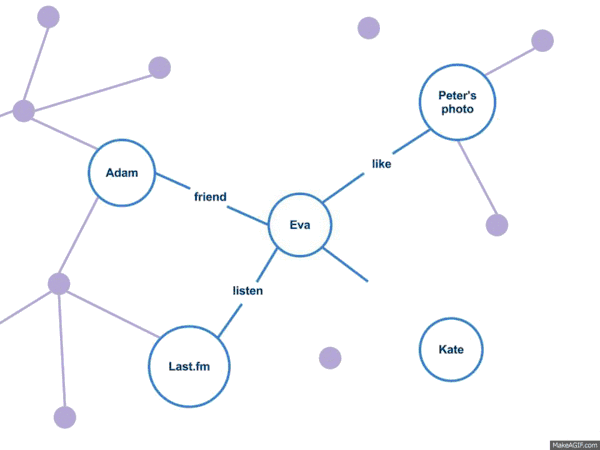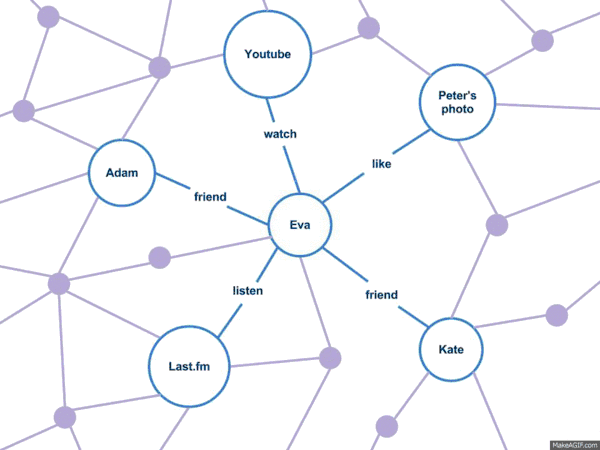
Неявний соціальний граф (англ. Implicit social graph) — це такий граф, який можна сформувати (вивести, обчислити) на основі взаємодій користувача зі своїми «друзями» та групами «друзів» в соціальній мережі. У цьому графі на відміну від звичайного соціального графа немає явної вказівки «друзів», тобто немає явних соціальних зв'язків[4].
Особливості соціального графа характеризується такими метриками, як: метрики взаємин, метрики зв'язків та сегментації. Для вирішення завдань на соціальному графі використовуються спеціальні моделі, за допомогою яких можна замінити «реальні» графи. За допомогою соціальних графів вирішують такі завдання, як: ідентифікація користувачів; соціальний пошук; генерація рекомендацій з вибору «друзів», медіа-контенту, новин, тощо; виявлення «реальних» зв'язків або збір відкритої інформації для моделювання графа. Обробка даних соціальних графів пов'язана з низкою проблем, як наприклад відмінності соціальних мереж, закритість соціальних даних.
Метрики
Говорячи про завдання на соціальному графі, вживають термін метрики, які в числовій формі відображають характеристики соціальних об'єктів, сегментів/груп об'єктів та їх зв'язків. Ці метрики використовують при проведенні аналізу соціальних мереж.
Взаємовідносини
Дані метрики подають характер взаємовідносин одного соціального об'єкта з іншими соціальними об'єктами.
- Гомофілія [5] (англ. Homophily) — ступінь, в якій користувач утворює зв'язки з подібними. Подібність може бути визначене за ст́аттю, віком, соціальним станом, освітнім рівнем тощо[6].
- Множинність (англ. Multiplexity) — число «множинних» зв'язків, в яких знаходяться користувачі[7]. Наприклад, два користувача, які товаришують та працюють разом, будуть мати «множинність», рівну 2[8]. «Множинність» пов'язують з «силою зв'язку».
- Взаємність (англ. Mutuality/Reciprocity) — ступінь, в якій користувачі взаємодіють між собою, відповідають взаємністю на дії один одного[9].
- Мережева закритість (англ. Network Closure) — ступінь, в якій друзі користувача є друзями один одному. Також її називають «мірою повноти реляційних тріад». Припущення того, що користувач знаходиться в мережевій закритості, називається Транзитивність. [10]
Зв'язки
Дані метрики відображають особливості зв'язків, як для окремих соціальних об'єктів, так і для графа в цілому.
- Міст (англ. Bridge) — користувач, чиї слабкі зв'язки заповнюють «структурні діри», що забезпечує єдиний зв'язок між іншими користувачами або кластерами (групами користувачів). Також через нього проходитиме найкоротший маршрут[11].
- Центральність — показник «важливості» або «впливу» певного користувача (кластера користувачів) всередині графа[12][13].
- Стандартні методи вимірювання «центральності» включають в себе центральність за посередництвом[14], центральність за близькістю[14], центральність за впливовістю, альфа-центральність та центральність за степенем[14][15].
- Густина (англ. Density) — частка прямих зв'язків у мережі по відношенню до загального числа можливих[16][17].
- Відстань (англ. Distance) — мінімальну кількість зв'язків, необхідних для встановлення наявності взаємозв'язку між двома окремими користувачами.
- Структурні діри (англ. Structural holes) — відсутність зв'язків між двома частинами мережі.
Сегментація
Дані метрики відображають характеристики соціального графа, поділеного на сегменти, які мають відмінні риси.
- Кліка (англ. Cliques) — група, в якій всі користувачі мають «прямі» зв'язки (вершини пов'язані (з'єднані) ребром) один до одного[18].
- Соціальне коло (англ. Social circles) — група, в якій не обов'язкові «прямі» зв'язки між користувачами[19].
- Коефіцієнт кластеризації (англ. Clustering coefficient) — ступінь ймовірності того, що два різних користувача, пов'язані з конкретним індивідуумом. Високий коефіцієнт кластеризації вказує на високу замкнутість групи, іншими словами, група може бути «клікою».
- Згуртованість (англ. Cohesion) — ступінь, в якій користувачі пов'язані між собою одним, загально-з'єднаним зв'язком, утворюючи соціальну згуртованість. Структурна згуртованість — вказує на таку єдину структуру групи, що видалення невеликої кількості користувачів веде до розриву групи[18].
Моделі
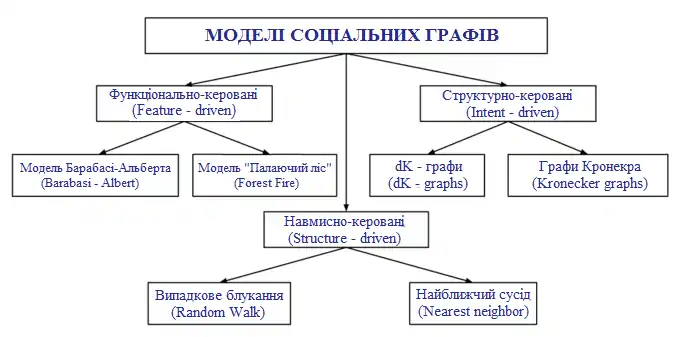
У цьому розділі наведені загальновідомі моделі графів, які потенційно можуть замінити «реальні» соціальний графи[20].
Функціонально-керовані моделі (англ. Feature-driven Models) націлені на відтворення статистичних характеристик графа, таких як ступовий розподіл та динамічні зміни щільності графа.
- Модель Барабаш — Альберт
- Модель «Палаючий ліс» (Forest Fire)
Навмисно-керовані моделі (англ. Intent-driven Models) сфокусовані на емуляцію процесу створення оригінального графа.
- Випадковий обхід/випадкові блукання (Random Walk)
- Найближчий сусід (Nearest Neighbor)
Структурно-керовані моделі (англ. Structure-driven Models) охоплюють статистичні дані зі структури графа, дозволяючи відповідному генератору відтворювати випадкові графи з тими ж структурними обмеженнями.
- Графи Кронекера (Kronecker graphs)
- dK-графи (dK-graphs)
Завдання
Ідентифікація користувачів
Виявлення профілів, що належать одній людині, в декількох соціальних мережах[21]. Вирішення цієї задачі дозволяє отримати більш повний соціальний граф, що може бути корисно в багатьох задачах, таких як:
- Соціальний пошук
- Генерація рекомендацій
Соціальний пошук
Пошук соціальних об'єктів (користувачів, їх даних, їх записів, тощо.), заснований на аналізі набору зв'язків, в яких знаходяться об'єкти котрі треба знайти[22].
Генерація рекомендацій
Важливим завданням є пошук точних алгоритмів генерації рекомендацій та пропозицій користувачам, які так само використовуються при створенні графа інтересів на основі соціального графа.
- Рекомендація друзів — користувачі рідко ділять свої контакти на соціальні групи, але, тим не менш, вони неявно ділять ці контакти на кластери, через їх взаємодії в рамках соціальної мережі[23].
- Рекомендації контенту — рекомендації медіа-контенту, спільнот, новин тощо[24].
Підхід до рекомендацій
Існує традиційний підхід в області рекомендаційних систем[25]:
- Колаборативна фільтрація[26] — полягає у формуванні списку рекомендованих об'єктів на основі думок користувачів, провідних себе схожим чином.
- Фільтрація вмісту — ґрунтується на характеристиках предмета та відомої про нього інформації.
- Соціальний підхід — відштовхуються від соціальних зв'язків користувачів.
Виявлення «справжніх» зв'язків
Застосування підходу «розвідки на основі відкритих джерел» (англ. Open source intelligence, OSINT) для виявлення істинних зв'язків між користувачами, тобто справжніх друзів, родичів тощо[27].
Збір інформації
Побудова соціального графа на основі даних, отриманих внаслідок парсинга веб-сервісів провайдерів соціальних мереж.
Для оцінювання завдання відносяться такі критерії[28]:
- Ефективність: наскільки швидко виявляють вузли/зв'язку внаслідок сканування,
- Чутливість: як різні соціальні мережі та кількість захищених/закритих користувачів («чорної діри») впливають на обхід,
- Відхилення: наскільки сильно відрізняються статистичні властивості підграфів, отриманих при обході, від властивостей вихідного графа.
При обході оцінюють такі фактори:
- Вибір вузлів: вузли є відправною точкою обходу. Важливо вибрати правильні вузли та порядок обходу черг, щоб уникнути низької якості сторінки,
- Алгоритми вибору вузлів: алгоритми вирішують, який вузол вибрати наступним. Часто використовувані алгоритми:
- Захищені користувачі: через закритість соціальних даних, можна пропустити велику частину соціального графа. Різні алгоритми обходів впливають на таких користувачів по-різному,
- Різні соціальні мережі: вони мають свої унікальні властивості, навіть якщо вони надають аналогічні послуги.
Проблеми
Відмінності соціальних мереж
Для задачі ідентифікації користувачів головною проблемою є відмінності соціальних мереж. Переважно грають роль семантика зв'язків між соціальними об'єктами та соціальні графи різних топологій[29].
Генерація рекомендацій
Основною проблемою генерації рекомендацій є проблема холодного старту — розрахунок рекомендації для нових соціальних об'єктів (користувачів, постів, медіа-контенту, тощо)[30].
Закритість соціальних даних
Головна проблема збору даних для соціального графа полягає в закритості соціальних мереж[31].
- По-перше, важко отримати соціальний граф від «провайдерів»[32] через цінність та захист законом соціальних даних.
- По-друге, великою проблемою є збір мільйонів списків контактів, профілів, фотографій, відео, тощо парсер. Багато «провайдерів» соціальних мереж використовують Single Page Application або безліч динамічних сторінок, що містять Ajax та DHTML, що створює дуже багато проблем для створення гнучкого парсера.
Див. також
Примітки
- Слово «медиа-контент» в словаре Академик
- Завдання ідентифікації користувачів в соціальних мережах, 2012, с. 3.
- Соціальний пошук, 2010, с. 199.
- Suggesting Friends, 2010, с. 2.
- Поняття гомофілія, 2012, с. 168-169.
- гомофілія, 2001, с. 415-444.
- Множинність, 1997, с. 673-693.
- Приклад множинності, 2003.
- Розуміння соціальних графів, 2012.
- Транзитивність, 2010, с. 855-869.
- Сила зв'язків, 1973, с. 1360-1380.
- Центральність, 2010, с. 32.
- Метрики для базового мережевого аналізу, 2011, с. 364-367.
- Є.В. Мелешко, В.С. Гермак, С.М. Охотний (2 жовтня 2016). Дослідження методів визначення центральності акторів у соціальних мережах для задач інформаційної безпеки. http://irbis-nbuv.gov.ua (укр.). Процитовано 17 січня 2021.
- Центральність вершин, 2010, с. 245.
- Аналіз соціальних мереж, 2006, с. B-11 — B-12.
- Соціальні мережі: техніки та додатки, 2010, с. 25.
- Кліка в аналізі соціальних мереж, 2011, с. 149.
- Метрики для базового мережевого аналізу, 2011, с. 346-347.
- Social Graph Models, 2010, с. 3-4.
- завдання ідентифікації користувачів в соціальних мережах, 2012, с. 2-4.
- Соціальний пошук, 2010, с. 431.
- Suggesting Friends, 2010, с. 2-7.
- Рекомендації треків у соціальних мережах, 2012, с. 34.
- підходи до рекомендацій, 2012, с. 8-13.
- Рекомендаційні системи на основі колаборативної фільтрації, 2002, с. 187.
- OSINT, 2012, с. 21-39.
- Crawling OSN, 2010, с. 1-7.
- Проблеми задачі ідентифікації користувачів, 2012, с. 13-17.
- Проблема холодного старту, 2012, с. 5-11.
- Crawling OSN, 2010, с. 1.
- Crawling OSN, 2010, с. 3.
Література
- M. Granovetter. The strength of weak ties. — American Journal of Sociology, 1973.
- Melville P.,Mooney R., Nagarajan R. Content-Boosted Collaborative Filtering for Improved Recommendations // University of Texas, USA : матеріали конф./AAAI-02, Austin, TX, USA, 2002. — 2002. — P. 187-192.
- J.M. Podolny, J.N. Baron. Resources and relationships: Social networks and mobility in the workplace. — American Sociological Review, 1997.
- N. McPherson, L. Smith-Lovin, J.M. Cook. Birds of a feather: Homophily in social networks. — Annual Reviews, Annual Review of Sociology, 2001.
- M. Kilduff, W. Tsai. Social networks and organisations. — Sage Publications, 2003. — P. 172.
- C. Kadushin. Social Network Analysis. — Headquarters, Department of the Army, Washington, DC, 2006. — ISBN 978-1-84787-395-8.
- A.-K. Pietiläinen, E. Oliver, J. LeBrun. ~redis/intranet/bibliography/middleware/pietilainen-mobiclique-2009.pdf MobiClique: Middleware for Mobile Social Networking. — WOSN'09, August 17, 2009, Barcelona, Spain, 2009.
- Xu, Guandong et al. Web Mining and Social Networking: Techniques and Applications. — Springer, 2010. — ISBN 978-1-4419-7734-2.
- D. Hansen, B. Shneiderman, M. A. Smith. Analyzing Social Media Networks with NodeXL. — Morgan Kaufmann, 2010. — С. 283. — ISBN 978-0-12-382229-1.
- Shaozhi Ye, Juan Lang, Felix Wu. Crawling Online Social Graphs. — APWEB'12, April 6-8, 2010, Busan, Korea, 2010.
- C. McCarthy. Facebook: One Social Graph to Rule Them All?. — CBS Interactive Inc., 2010.
- T. Opsahl, F. Agneessens, J. Skvoretz. Node centrality in weighted networks: Generalizing degree and shortest paths. — Social Networks, 2010.
- M. Roth, A. Ben-David, D. Deutscher. Suggesting Friends Using the Implicit Social Graph. — KDD'10, July 25-28, 2010, Washington, DC, USA., 2010.
- A. Sala, L. Cao, C. Wilson, R. Zablit, H. Zheng, B. Y. Zhao. Measurement-calibrated Graph Models for Social Network Experiments. — WWW 2010, April 26-30, 2010, Raleigh, North Carolina, USA, 2010.
- D. Horowitz, Sepandar D. Kamvar. The Anatomy of a Large-ScaleSocialSearch Engine. — WWW 2010, April 26-30, 2010, Raleigh, North Carolina, USA., 2010.
- F.J. Flynn, R.E. Reagans, L. Guillory. Do you two know each other? Transitivity, homophily, and the need for (network) closure.. — Journal of Personality and Social Psychology, 2010.
- J. Ugander, B. Karrer, L. Backstrom, C. Marlow. The Anatomy of the Facebook Social Graph. — Cornell University Library, 2011.
- My T. Thai, Panos M. Pardalos. Handbook of Optimization in Complex Networks: Communication and Social Networks. — Springer, 2011. — С. 541. — ISBN 978-1-4614-0856-7.
- P. J. Carrington, J. Scott. The Sage Handbook of Social Network Analysis. — SAGE, 2011. — С. 640. — ISBN 978-1-84787-395-8.
- D. Schioberg, F. Schneider, H. Schioberg, S. Schmid, S. Uhlig, Anja Feldmann. Tracing the Birth of an OSN: Graph and Profile Analysis in Google+. — WebSci 2012, June 22-24, 2012, Evanston, Illinois, USA, 2012.
- M. P. Zillman. Online Social Networks. — Virtual Private Library, 2012.
- B. R. Holland. Enabling Open Source Intelligence (OSINT) in private social networks. — Iowa State University, Ames, Iowa, 2012.
- C. Kadushin. Understanding social networks: Theories, concepts, and findings. — Oxford : Oxford University Press, 2012. — С. 288.
- В.М. Сазанів. Соціальні мережі як нова суспільна сфера. Системний аналіз та прогноз. — М. : Лабораторія СВМ, 2010. — С. 180.
- С. Бартуков, А. Коршунов. Ідентифікація користувачів соціальних мереж в Інтернет на основі соціальних зв'язків. — Інститут системного програмування Російської академії наук, 2012.
- А.А. Дзюба. Рекомендації треків у соціальних мережах. — Санкт-Петербурзький Державний Університет, 2012.
- Н. В. Богатир. Вкоріненість і за її межами: вплив мереж. — Міжнародна конференція «Вкоріненість і за її межами: пояснюють чи соціологічні теорії економічну реальність ?»Жовтень 25-28, 2012, Москва, Росія, 2012. — С. 168-169.
