Біноміальний коефіцієнт

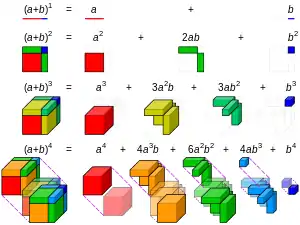
Біноміальні коефіцієнти — коефіцієнти в розкладі $\ (1+x)^{n}$ по степенях $\ x$ (так званий біном Ньютона):

(1+x)^{n}={n \choose 0}+{n \choose 1}x+{n \choose 2}x^{2}+\cdots +{n \choose n}x^{n}=\sum _{k=0}^{n}{n \choose k}x^{k}.

Біноміальні коефіцієнти розташовані у вигляді трикутника Паскаля.

Візуалізація біноміальних коефіцієнтів до 4 степеня

Біноміальний коефіцієнт є узагальненням кількості невпорядкованих виборів $C_{n}^{k}$ , що визначена тільки для невід'ємних цілих чисел $n$ , $k$ , тобто $\ n+1\in \mathbb {N}$ та $\ k+1\in \mathbb {N} .$ У явному вигляді для $0\leq k\leq n$ :

{n \choose k}=C_{n}^{k}={\frac {n!}{k!\;(n-k)!}}

,

де $n!$ та $k!$ — факторіали чисел $n$ і $k$ .

Явні формули

Обчислюючи коефіцієнти в розкладі $(1+x)^{n}$ у степеневий ряд, можна отримати явні формули для біноміальних коефіцієнтів $\textstyle {\binom {n}{k}}$ .

Для всіх дійсних чисел n і цілих чисел k:

{\binom {n}{k}}={\begin{cases}{\frac {n(n-1)(n-2)\cdot \ldots \cdot (n-k+1)}{k!}},&k\geqslant 0,\\0,&k<0,\end{cases}}

де $k!$ позначає факторіал числа k.

Для невід'ємних цілих n і k також справедливі формули:

{\binom {n}{k}}={\begin{cases}{\frac {n!}{k!(n-k)!}},&0\leqslant k\leqslant n,\\0,&k>n.\end{cases}}

Для цілих від'ємних показників коефіцієнти розкладу бінома $(1+x)^{-n}$ рівні

{\binom {-n}{k}}={\begin{cases}(-1)^{k}\cdot {\frac {(n+k-1)!}{k!(n-1)!}},&k\geqslant 0,\\0,&k<0.\end{cases}}

Трикутник Паскаля

Тотожність ${n \choose k}={n-1 \choose k-1}+{n-1 \choose k}$ дозволяє розташувати біноміальні коефіцієнти для невід'ємних $n$ , $k$ у вигляді трикутника Паскаля, в якому кожне число рівне сумі двох, що стоять на рядок вище:

{\begin{matrix}n=0:&&&&&1&&&&\\n=1:&&&&1&&1&&&\\n=2:&&&1&&2&&1&&\\n=3:&&1&&3&&3&&1&\\n=4:&1&&4&&6&&4&&1\\\vdots &&\vdots &&\vdots &&\vdots &&\vdots &\end{matrix}}

Трикутна таблиця, запропонована Паскалем в «Трактаті про арифметичний трикутник» (1654), відрізняється від описаної тут поворотом на 45°. Таблиці для зображення біноміальних коефіцієнтів були відомі й раніше.

Властивості

Твірні функції

Для фіксованого значення n твірною функцією послідовності біноміальних коефіцієнтів ${\tbinom {n}{0}},\;{\tbinom {n}{1}},\;{\tbinom {n}{2}},$ … є

\sum _{k=0}^{\infty }{\binom {n}{k}}x^{k}=(1+x)^{n}.

Для фіксованого значення k твірною функцією послідовності коефіцієнтів ${\tbinom {0}{k}},\;{\tbinom {1}{k}},\;{\tbinom {2}{k}},$ … є

Двовимірною твірною функцією біноміальних коефіцієнтів ${\tbinom {n}{k}}$ для цілих $n,k$ є

\sum _{n,k}{\binom {n}{k}}x^{k}y^{n}={\frac {1}{1-y-xy}},

або

\sum _{n=0}^{\infty }\sum _{k=0}^{n}{\binom {n}{k}}x^{k}y^{n}={\frac {1}{1-y-xy}}.

Подільність

Із теореми Люка випливає, що:

коефіцієнт $\textstyle {\binom {n}{k}}$ непарний $\iff$ в двійкового запису числа k одиниці не стоять у тих розрядах, де в числі n стоять нулі;
коефіцієнт $\textstyle {\binom {n}{k}}$ не кратний простому число p $\iff$ в p-ковому записі числа k всі розряди не перевищують відповідних розрядів числа n;
у послідовності біноміальних коефіцієнтів $\textstyle {\binom {n}{0}},\;{\binom {n}{1}},\;\ldots ,\;{\binom {n}{n}}$ $\text{[math]}$ :
- всі числа не кратні заданому простому p $\iff$ число $n$ можна подати у вигляді $mp^{k}-1$ , де натуральне число m < p;
- всі числа, крім першого й останнього, кратні даному простому p $\iff$ $n=p^{k}$ ;
- кількість непарних чисел дорівнює степеню двійки, показник якої дорівнює кількості одиниць у двійковому записі числа n;
- парних і непарних чисел не може бути порівну;
- кількість чисел, не кратних простому p, дорівнює $(a_{1}+1)\cdots (a_{m}+1)$ , де числа $a_{1},\;\ldots ,a_{m}$ — розряди p-кового запису числа n; а число $\textstyle m=\lfloor \log _{p}{n}\rfloor +1,$ де $\lfloor \cdot \rfloor$ — функція «підлога» — це довжина даного запису.

Тотожності

${n \choose k}={n-1 \choose k-1}+{n-1 \choose k}$
${n \choose k}={\frac {n}{n-k}}{n-1 \choose k}$
${n \choose 0}+{n \choose 1}+\cdots +{n \choose n}=2^{n}$
${n \choose 0}+{n \choose 2}+\cdots +{n \choose 2\lfloor n/2\rfloor }=2^{n-1}$
${n \choose 0}^{2}+{n \choose 1}^{2}+\cdots +{n \choose n}^{2}={2n \choose n}$
$\sum _{k=0}^{n}{r \choose m+k}{s \choose n-k}={r+s \choose m+n}$ (згортка Вандермонда)

Біном Ньютона і наслідки

${n \choose 0}+{n \choose 1}+\ldots +{n \choose n}=2^{n},$ де $n\in \mathbb {N} .$
$\sum _{i+j=m}{\binom {n}{j}}{\binom {n}{i}}(-1)^{j}={\begin{cases}{\binom {n}{m/2}},&{\text{якщо}}\ m\equiv 0{\pmod {2}},\\0,&{\text{якщо}}\ m\equiv 1{\pmod {2}}.\end{cases}}$
$\sum _{j=k}^{n}{\binom {n}{j}}(-1)^{j}=(-1)^{k}{\binom {n-1}{k-1}}.$
${n \choose 0}-{n \choose 1}+\ldots +(-1)^{n}{n \choose n}=0,$ де $n\in \mathbb {N} .$
Сильніша тотожність: ${n \choose 0}+{n \choose 2}+\ldots +{n \choose 2\lfloor n/2\rfloor }=2^{n-1},$ де $n\in \mathbb {N} .$
$\sum _{k=-a}^{a}(-1)^{k}{2a \choose k+a}^{3}={\frac {(3a)!}{(a!)^{3}}},$

а в загальнішому вигляді

\sum _{k=-a}^{a}(-1)^{k}{a+b \choose a+k}{b+c \choose b+k}{c+a \choose c+k}={\frac {(a+b+c)!}{a!\,b!\,c!}}.

Згортка Вандермонда і наслідки

$\sum _{k}{r \choose m+k}{s \choose n-k}={r+s \choose m+n}$ (згортка Вандермонда), де $m,n\in \mathbb {Z} ,$ а $r,s\in \mathbb {R} .$

Це тотожність виходить обчисленням коефіцієнта при $x^{m+n}$ у розкладі $(1+x)^{r}(1+x)^{s}$ з урахуванням тотожності $(1+x)^{r+s}=(1+x)^{r}(1+x)^{s}.$ Сума береться за всіма цілими $k$ , для яких $\textstyle {r \choose m+k}{s \choose n-k}\neq 0.$ Для довільних дійсних $r$ , $s$ число ненульових доданків у сумі буде скінченним.

${n \choose 0}{a \choose a}-{n \choose 1}{a+1 \choose a}+\ldots +(-1)^{n}{n \choose n}{a+n \choose a}=(-1)^{n}{a \choose n}$ .
загальніша тотожність: $\sum _{i=0}^{p}(-1)^{i}{p \choose i}\prod _{m=1}^{n}{i+s_{m} \choose s_{m}}=0$ , якщо $\sum _{m=1}^{n}{s_{m}}<p$ .
${n \choose 0}^{2}+{n \choose 1}^{2}+\ldots +{n \choose n}^{2}={2n \choose n}.$

Інші тотожності

$\sum _{k=1}^{n}{\frac {(-1)^{k-1}}{k}}{n \choose k}=\sum _{k=1}^{n}{\frac {1}{k}}=H_{n}$ — n- е гармонічне число.
Мультисекція ряду $(1+x)^{n}$ дає тотожність, що виражає суму біноміальних коефіцієнтів із довільним кроком s і зміщенням t $(0\leqslant t<s)$ у вигляді скінченної суми з s доданків:

{\binom {n}{t}}+{\binom {n}{t+s}}+{\binom {n}{t+2s}}+\ldots ={\frac {1}{s}}\sum _{j=0}^{s-1}\left(2\cos {\frac {\pi j}{s}}\right)^{n}\cos {\frac {\pi (n-2t)j}{s}}.

Виконуються рівності[1]:

{\begin{alignedat}{2}{\binom {n}{3}}&={\frac {n(n-1)(n-2)}{\color {Green}2}}-\sum _{i=2}^{n-1}{(n-i)(n-i+1)}=\\&=n(n-1)(n-2)-\sum _{i=2}^{n-1}{(n-i)({\color {Green}2}n-i+1)}=\\&=3{\binom {n}{3}}-2{\binom {n}{3}};\\\end{alignedat}}

{\begin{alignedat}{2}{\binom {n}{4}}&={\frac {n(n-1)(n-2)(n-3)}{\color {Green}2}}-\sum _{i=3}^{n-1}{(n-i)\left(n(n-1)-\sum _{i_{0}=1}^{i-2}i_{0}\right)}=\\&=n(n-1)(n-2)(n-3)-\sum _{i=3}^{n-1}{(n-i)\left({\color {Green}2}n(n-1)-\sum _{i_{0}=1}^{i-2}i_{0}\right)}=\\&=24{\binom {n}{4}}-23{\binom {n}{4}};\\\end{alignedat}}

{\begin{alignedat}{2}{\binom {n}{5}}&={\frac {n(n-1)(n-2)(n-3)(n-4)}{\color {Green}2}}-\\&-\sum _{i=4}^{n-1}{(n-i)\left(n(n-1)(n-2)-\sum _{i_{0}=1}^{i-3}\sum _{i_{1}=1}^{i_{0}}i_{1}\right)}=\\&=n(n-1)(n-2)(n-3)(n-4)-\\&-\sum _{i=4}^{n-1}{(n-i)\left({\color {Green}2}n(n-1)(n-2)-\sum _{i_{0}=1}^{i-3}\sum _{i_{1}=1}^{i_{0}}i_{1}\right)}=\\&=120{\binom {n}{5}}-119{\binom {n}{5}}.\end{alignedat}}

Звідки випливає:

{\binom {n}{3}}={\frac {\sum \limits _{i=2}^{n-1}{(n-i)(2n-i+1)}}{2}}={\frac {\sum \limits _{i=2}^{n-1}{(n-i)\left(2A_{n}^{1}-{\binom {i-1}{1}}\right)}}{2}};

{\binom {n}{4}}={\frac {\sum \limits _{i=3}^{n-1}{(n-i)\left(2n(n-1)-\sum \limits _{i_{0}=1}^{i-2}i_{0}\right)}}{23}}={\frac {\sum \limits _{i=3}^{n-1}{(n-i)\left(2A_{n}^{2}-{\binom {i-1}{2}}\right)}}{23}};

{\begin{alignedat}{2}&{\binom {n}{5}}={\frac {\sum \limits _{i=4}^{n-1}{(n-i)\left(2n(n-1)(n-2)-\sum \limits _{i_{0}=1}^{i-3}\sum \limits _{i_{1}=1}^{i_{0}}i_{1}\right)}}{119}}=\\&={\frac {\sum \limits _{i=4}^{n-1}{(n-i)\left(2A_{n}^{3}-{\binom {i-1}{3}}\right)}}{119}};\\\end{alignedat}}

{\binom {n}{k}}={\frac {\sum \limits _{i=k-1}^{n-1}{(n-i)\left(2A_{n}^{k-2}-{\binom {i-1}{k-2}}\right)}}{k!-1}},

де $A_{n}^{k}$ — кількість розміщень із n по k.

Матричні співвідношення

Якщо взяти квадратну матрицю, відрахувавши N елементів по катетах трикутника Паскаля і повернувши матрицю на будь-який з чотирьох кутів, то детермінант цих чотирьох матриць дорівнює ±1 за будь-якого N, причому детермінант матриці з вершиною трикутника у верхньому лівому куті дорівнює 1.

У матриці ${\begin{bmatrix}{\tbinom {i+j}{i}}\end{bmatrix}}$ числа на діагоналі $i+j=const$ повторюють числа рядків трикутника Паскаля $(i,j=0,1,\ldots )$ . Її можна розкласти в добуток двох строго діагональних матриць: нижньотрикутної та одержуваної з неї транспонуванням. А саме:

{\begin{bmatrix}{\binom {i+j}{i}}\end{bmatrix}}=UU^{T},

де $U={\begin{bmatrix}{\tbinom {i}{j}}\end{bmatrix}}$ . Обернена матриця до $U$ має вигляд:

U^{-1}={\begin{bmatrix}(-1)^{i+j}{\binom {i}{j}}\end{bmatrix}}.

Таким чином, матрицю, обернену до ${\begin{bmatrix}{\tbinom {i+j}{i}}\end{bmatrix}}$ , можна розкласти в добуток двох строго діагональних матриць: перша матриця — верхньотрикутна, а друга виходить з першої транспонуванням, що дозволяє дати явний вираз для обернених елементів:

{\begin{bmatrix}{\binom {i+j}{i}}\end{bmatrix}}_{m,n}^{-1}=\sum _{k=0}^{p}(-1)^{m+n}{\binom {k}{m}}{\binom {k}{n}}

, де i, j, m, n = 0..p.

Елементи оберненої матриці змінюються за зміни її розміру і, на відміну від матриці ${\begin{bmatrix}{\tbinom {i+j}{i}}\end{bmatrix}}$ , недостатньо приписати новий рядок і стовпець. Стовпець j матриці ${\begin{bmatrix}{\tbinom {i+j}{i}}\end{bmatrix}}$ є многочленом степеня j за аргументом i, отже, перші p стовпців утворюють повний базис у просторі векторів довжини p+1, чиї координати можна інтерполювати многочленом степеня рівного або меншого ніж p-1. Нижній рядок матриці ${\begin{bmatrix}{\binom {i+j}{i}}\end{bmatrix}}_{m,n}^{-1}$ ортогональний до будь-якого такого вектора.

{\begin{bmatrix}{\binom {i+j}{i}}\end{bmatrix}}_{p,n}^{-1}=\sum _{k=0}^{p}(-1)^{p+n}{\binom {k}{p}}{\binom {k}{n}}=(-1)^{p+n}{\binom {p}{n}}

\sum _{n=0}^{p}(-1)^{p+n}{\binom {p}{n}}{P}_{a}(n)=0

при

a<p

, де

{P}_{a}(n)

многочлен степеня

a

.

Якщо довільний вектор довжини $p+1$ можна інтерполювати многочленом степеня $i<p$ , то скалярний добуток з рядками $i+1,i+2,\dots ,p$ (нумерація з 0) матриці ${\begin{bmatrix}{\binom {i+j}{i}}\end{bmatrix}}_{m,n}^{-1}$ дорівнює нулю. Використовуючи тотожність вище і рівність одиниці скалярного добутку нижнього рядка матриці ${\begin{bmatrix}{\binom {i+j}{i}}\end{bmatrix}}_{m,n}^{-1}$ на останній стовпець матриці ${\begin{bmatrix}{\tbinom {i+j}{i}}\end{bmatrix}}$ , маємо:

\sum _{n=0}^{p}(-1)^{p+n}{\binom {p}{n}}{n}^{p}=p!.

Для показника, більшого від p, можна задати рекурентну формулу:

\sum _{n=0}^{p}(-1)^{p+n}{\binom {p}{n}}{n}^{p+a}=p!{P}_{2a}(p)={f}_{a}(p),

де многочлен

{P}_{2a+2}(p)=\sum _{x=1}^{p}x{P}_{2a}(x);\quad a\geqslant 0;\quad {P}_{0}(p)=1.

Для доведення спершу доводиться тотожність:

{f}_{a}(p+1)=\sum _{x=0}^{a}{(p+1)}^{x+1}{f}_{a-x}(p).

Якщо потрібно знайти формулу не для всіх показників степеня, то

{P}_{2a}(p)={\frac {p}{{2}^{a}}}{\binom {p+a}{a}}{Q}_{a-1}(p);\quad a>0.

Старший коефіцієнт ${Q}_{a-1}(p)$ дорівнює 1, щоб знайти інші коефіцієнти, знадобиться $a-1$ значень:

{Q}_{a-1}(p)=p(p+1){T}_{a-3}(p)

для

a\equiv 1{\pmod {2}};a\geqslant 3.

Цілозначні многочлени

Біноміальні коефіцієнти ${\tbinom {x}{0}}=1,{\tbinom {x}{1}}=x,{\tbinom {x}{2}}={\tfrac {x^{2}}{2}}-{\tfrac {x}{2}},$ … є цілозначними многочленами від $x$ , тобто, набувають цілих значень за цілих значень $x,$ — це неважко зрозуміти, наприклад, за трикутником Паскаля. Більш того, вони утворюють базис цілозначних многочленів, у якому всі цілозначні многочлени виражаються як лінійні комбінації з цілими коефіцієнтами[2].

Разом з тим, стандартний базис $1,x,x^{2},$ … не дозволяє виразити всіх цілочисельних многочленів, якщо використовувати тільки цілі коефіцієнти, оскільки вже ${\tbinom {x}{2}}={\tfrac {x^{2}}{2}}-{\tfrac {x}{2}}$ має дробові коефіцієнти при степенях $x$ .

Цей результат узагальнюється на многочлени багатьох змінних. А саме, якщо многочлен $R(x_{1},\dots ,x_{m})$ степеня $k$ має дійсні коефіцієнти і набуває цілих значень за цілих значень змінних, то

R(x_{1},\dots ,x_{m})=P\left({\binom {x_{1}}{1}},\dots ,{\binom {x_{1}}{k}},\dots ,{\binom {x_{m}}{1}},\dots ,{\binom {x_{m}}{k}}\right),

де $P$ — многочлен із цілими коефіцієнтами.[3]

Асимптотика і оцінки

${2n \choose n}\sim {\frac {2^{2n}}{\sqrt {\pi n}}}$
$\sum _{k=0}^{m}{n \choose k}\leq {\frac {n}{(n/2-m)^{2}}}2^{n-3}$ при $m\leq n/2$ (нерівність Чебишева)
$\sum _{k=0}^{m}{n \choose k}\leq 2^{nH(m/n)}$ (ентропійна оцінка), де $H(x)=-x\log _{2}x-(1-x)\log _{2}(1-x)$ — ентропія.
$\sum _{k=0}^{n/2-\lambda }{n \choose k}\leq 2^{n}e^{-2\lambda ^{2}/n}$ (нерівність Чернова)

Алгоритми обчислення

Біноміальні коефіцієнти можуть бути обчислені за допомогою тотожності ${n \choose k}={n-1 \choose k}+{n-1 \choose k-1}$ , якщо на кожному кроці зберігати значення ${n \choose k}$ для $k=0,1,\dots ,n$ . Цей алгоритм особливо ефективний, якщо необхідно отримати всі значення ${n \choose k}$ при фіксованому $n$ . Алгоритм потребує $\ O(n)$ пам'яті ( $\ O(n^{2})$ для обчислення всієї таблиці) і $\ O(n^{2})$ часу.

Інший спосіб ґрунтується на тотожності ${n \choose k}={\frac {n}{n-k}}{n-1 \choose k}$ . Він дозволяє обчислити значення ${n \choose k}$ при фіксованому $k$ . Алгоритм потребує $\ O(1)$ пам'яті і $\ O(k)$ часу.

Узагальнення

Оскільки для $\ n+1\in \mathbb {N$ , то значення біноміального коефіцієнта можна визначити для усіх комплексних чисел $\ n\in \mathbb {C}$ та $\ k\in \mathbb {C}$ :

{n \choose k}={\frac {\Gamma (n+1)}{\Gamma (k+1)\Gamma (n-k+1)}}

Явні формули для обчислення біноміальних коефіцієнтів для цілих чисел $\ n$ та $\ k$ :

{n \choose k}={\frac {n!}{k!\;(n-k)!}}

для

0\leq k\leq n

;

{n \choose k}=0

для

\ k<0

або

0\leq n<k

;

{n \choose k}=(-1)^{k}{-n+k-1 \choose k}

для

n<0\leq k

.

Біноміальні коефіцієнти часто зустрічаються в комбінаторних задачах і теорії імовірностей.

Узагальненням біноміального коефіцієнта є поліноміальний коефіцієнт.

Генерація на C++

#include <iostream>
#include <string>

using namespace std;

void C(int n, int m, int startAt = 1, string s = "") {
	for (int i = startAt; i <= n - m + 1; i++) {
		if (1 == m)
			cout << s + (char)(i+'0') << endl;
		else
			C(n, m - 1, i + 1, s + (char)(i+'0'));
	}	
}

int main() {
	C(7, 3);
	
	return 0;
}

Див. також

Примітки

Четырёхмерные таблицы в комбинаторике — два странных способа посчитать сочетания. habr.com. 30 листопада 2020. Процитовано 27 березня 2021.
Прасолов В. В. Глава 12. Целозначные многочлены // Многочлены. — М. : МЦНМО, 1999, 2001, 2003.
Ю. Матиясевич. Десятая проблема Гильберта. — Наука, 1993. — С. 20,185,194.

Джерела

Завало С. Т. (1972). Елементи аналізу. Алгебра многочленів. Київ: Радянська школа. с. 462. (укр.)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[example-1] Четырёхмерные таблицы в комбинаторике — два странных способа посчитать сочетания. habr.com. 30 листопада 2020. Процитовано 27 березня 2021.

[2] Прасолов В. В. Глава 12. Целозначные многочлены // Многочлены. — М. : МЦНМО, 1999, 2001, 2003.

[3] Ю. Матиясевич. Десятая проблема Гильберта. — Наука, 1993. — С. 20,185,194.