Задача про розбиття

Ми хочемо визначити, чи існує підмножина S, котра дорівнює ${\displaystyle \lfloor K/2\rfloor }$. Нехай:

p(i, j) буде Істина (True), якщо мультимножина { x₁, ..., x_j } дорівнює i , та Хибно (False), якщо навпаки.

Тоді p(${\displaystyle \lfloor K/2\rfloor }$, n) - це Істина тоді та тільки тоді, коли існує мультимножина S, котра дорівнює ${\displaystyle \lfloor K/2\rfloor }$. Метою нашого алгоритму буде обчислення p(${\displaystyle \lfloor K/2\rfloor }$, n). Для цього ми маємо наступне рекурентне співвідношення:

p(i, j) істинно, якщо p(i, j − 1) істинно або p(i − x_j, j − 1) істинно,

p(i, j) хибне, навпаки.

Це пояснюється наступним чином: є деяка підмножина S, яке підсумовує з i, використовуючи числа

x₁, ..., x_j

Тоді та тільки тоді, коли виконано одну з наступних умов:

Існує підмножина { x₁, ..., x_j-1 } , котра дорівнює i;

Існує підмножина { x₁, ..., x_j-1 } котра дорівнює i − x_j, коли x_j + сума підмножини = i.

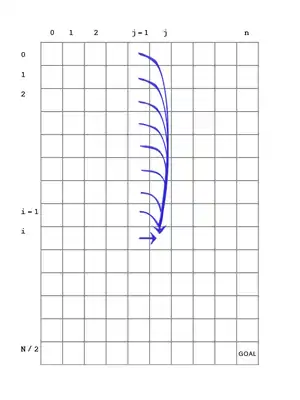
Алгоритм полягає в тому, щоб створити таблицю розміру ${\displaystyle \lfloor K/2\rfloor }$ по n , що містить значення повторення. Пам'ятайте, що K - це розмір суми, а N - це . кількість елементів. Коли вся таблиця заповнена, поверніть P(${\displaystyle \lfloor K/2\rfloor }$, n). Нижче наведено зображення таблиці P. Існує синя стрілка від одного блоку до іншого, якщо значення цільового блоку може залежати від значення вихідного блоку. Ця залежність є властивістю рекурентного співвідношення.

Залежність записів у таблиці (i, j)

INPUT:  A list of integers S
OUTPUT: True if S can be partitioned into two subsets that have equal sum
1 function find_partition(S):
2     n ← |S|
3     K ← sum(S)
4     P ← empty boolean table of size (${\displaystyle \lfloor K/2\rfloor }$ + 1) by (n + 1)
5     initialize top row (P(0,x)) of P to True
6     initialize leftmost column (P(x, 0)) of P, except for P(0, 0) to False
7     for i from 1 to ${\displaystyle \lfloor K/2\rfloor }$
8         for j from 1 to n
9             if (i-S[j-1]) >= 0
10               P(i, j) ← P(i, j-1) or P(i-S[j-1], j-1)
11            else
12               P(i, j) ← P(i, j-1)
13    return P(${\displaystyle \lfloor K/2\rfloor }$, n)

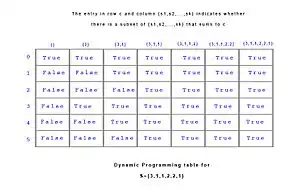
Нижче наведена таблиця P для прикладу, що використовується вище S = {3, 1, 1, 2, 2, 1}:

Результат виконання прикладу алгоритму на таблиці P

Цей алгоритм працює з часом O(K N), де N - кількість елементів у наборі вхідних даних та K - сума елементів у вхідній множині.

Алгоритм може бути розширений до k-задачі багаторозбиття, але потім приймає O(n(k − 1)m^{k − 1}) пам'ять, де m - найбільше число на вході, що робить його непрактичним навіть для k = 3 , якщо входи не є дуже маленькими числами. [3]

Цей алгоритм можна узагальнити для вирішення задачі про суми підмножин.

Один з підходів до задачі, що імітує те, як діти вибирають команди для гри, — це жадібний алгоритм, який виконує ітерацію за номерами в порядку убування, привласнюючи кожному з них те, що підмножина має меншу суму. Цей підхід має час роботи  O(n log n). Ця евристика добре працює на практиці, коли цифри в наборі приблизно того ж розміру, що і потужність, або менше, але не гарантується, що буде створений найкращий розділ. Наприклад, якщо ввести S = {4, 5, 6, 7, 8} як вхідні дані, цей жадібний алгоритм розбив би S на підмножини {4, 5, 8} та {6, 7}; однак, S має точно збалансоване розбиття на підмножини {7, 8} та {4, 5, 6}.

Відомо, що цей жадібний підхід дає ⁷⁄₆-наближення до оптимального рішення версії оптимізації; Тобто, якщо жадібний алгоритм виводить два набори A та B, то max(∑A, ∑B) ≤ 76 OPT, де OPT це розмір більшого набору в найкращому можливому розділі.[4]Нижче наведено приклад (написаний на мові Python) для жадібного алгоритму..

def find_partition(int_list):
    "returns: An attempt at a partition of `int_list` into two sets of equal sum"
    A = set()
    B = set()
    for n in sorted(int_list, reverse=True):
        if sum(A) < sum(B):
           A.add(n)
        else:
           B.add(n)
    return (A, B)

Цей алгоритм може бути поширений на випадок k > 2 множин: для того, щоб узяти k найбільших елементів і для кожного розбиття їх розширює розділ, послідовно додаючи інші елементи в залежності від того, який набір менше. (Проста версія вище відповідає k = 2.) Ця версія працює в часі O(2^k n²) і, як відомо, дає (k + 2)(k + 1) наближення.[4] Таким чином, ми маємо схему наближення поліноміального часу (PTAS)для завдання про розбиття чисел, хоча це не повністю поліноміальна схема наближення часу (час роботи є експоненціальним у гарантованій задачі наближення). Однак існують варіанти цієї ідеї, які є повністю поліноміальними схемами апроксимації для завдання підмножини, а отже, і для завдання розбиття.[5]

Іншою евристикою є метод найбільшої різниці (largest differencing method, LDM),[6] що також має назву евристика Кармаркар—Карпа, за прізвищами пари вчених, що опублікували роботу по цій темі в 1982 році.[7] LDM працює в два етапи. Перша фаза алгоритму приймає два найбільших числа від входу і замінює їх їхньою різницею. Це повторюється до тих пір, поки не залишиться тільки одне число. Заміна є рішення розмістити два числа в різних наборах, не вдаючись до негайного визначення того, в якому з них встановлено. В кінці першого етапу єдиним числом, що залишилося, буде різниця двох сум підмножини. Друга фаза реконструює фактичне рішення.[2]

Евристика різниць працює краще, ніж жадібна, але все ще погано для випадків, коли числа є експонентними за розміром набору.[2]

Наступна програма на Java реалізує перший етап Кармаркар—Карпа. Він використовує купу, щоб знайти пару найбільших чисел, які залишилися.

int karmarkarKarpPartition(int[] baseArr) {	
    // create max heap	
    PriorityQueue<Integer> heap = new PriorityQueue<Integer>(baseArr.length, REVERSE_INT_CMP);

    for (int value : baseArr) {		
        heap.add(value);	
    }

    while(heap.size() > 1) {
        int val1 = heap.poll();	
        int val2 = heap.poll();	
        heap.add(val1 - val2);
    }

    return heap.poll();
}

Існують також алгоритми будь-якого часу, засновані на евристичному різницевої аналізі, які спочатку знаходять рішення, повернене евристикою разностного аналізу, потім знаходять прогресивно кращі рішення в міру того, як дозволяє час (можливо, вимагаючи експоненціального часу для досягнення оптимальності для найгірших випадків).[8]

Пов'язана з цим задача, в чомусь схожа на парадокс днів народження, полягає у визначенні розміру вхідної множини так, щоб ймовірність існування розв'язку була 50%, за припущення, що кожен елемент в наборі вибирається випадково за рівномірним розподілом між 1 і деяким заданим значенням.

Вирішення цієї задачі може бути нелогічним, як парадокс дня народження. Наприклад, якщо елементи вибираються випадковим чином в межах від 1 до 1 мільйона, інтуїція багатьох людей полягає в тому, що відповідь знаходиться в тисячах, десятках або навіть в сотнях тисяч, тоді як правильна відповідь становить приблизно 23 (див. Парадокс днів народження § апроксимація).^{[джерело?]}