Задача про стопку цегли

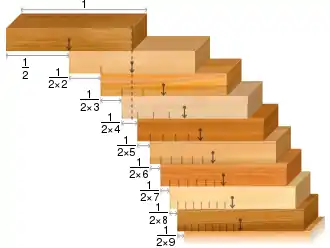
В ідеальному випадку з тільки одним ідеально прямокутним блоком на кожному рівні звисання дорівнює ${\displaystyle \sum _{i=1}^{N}{\frac {1}{2i}}}$ ширини блоку[2]. Ця сума складає половину часткової суми гармонійного ряду. Оскільки гармонійний ряд розходиться, максимальне звисання прямує до нескінченності з ростом ${\displaystyle N}$, тобто можна досягти будь-якого завгодно великого звису при достатній кількості блоків. У кожному конкретному випадку максимальне звис приблизно дорівнює ${\displaystyle {\frac {1}{2}}\ln N}$, тобто пропорційний натуральному логарифму числа блоків.

Порівняння рішень задачі з трьома блоками, з одним (зверху) і декількома (знизу) блоками на рівні

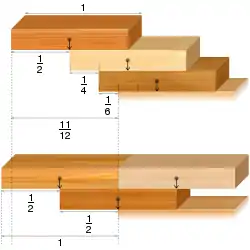
Додаткові блоки на рівні можуть використовуватися як противага і давати більше звисання, ніж варіант з одним блоком на рівні. Навіть для трьох блоків, укладання двох врівноважених блоків поверх іншого блоку, може дати звис в один блок, в той час як в простому ідеальному випадку — не більше ${\displaystyle {\frac {11}{12}}}$. У 2007 році Майк Патерсон з співавторами показали, що максимальний звис, який може бути досягнутий за допомогою декількох блоків на рівні, асимптотично дорівнює ${\displaystyle c{\sqrt[{3}]{N}}}$, тобто пропорційний кубічному кореню з числа блоків, на відміну від простого випадку, коли звис пропорційний логарифму кількості блоків.