Квантовий ефект Холла в графені

Рівні Ландау в графені описуються рівнянням Дірака для графену з врахуванням сильного магнітного поля, яке можна записати у вигляді[5]:

${\displaystyle [{\vec {\sigma }}\cdot (i\hbar v_{F}{\vec {\nabla }}+{\frac {e}{c}}{\vec {A}})]\psi (x,y)=\varepsilon \psi (x,y),}$

де використовується калібровка Ландау для векторного потенціалу ${\displaystyle {\vec {A}}=(-By,0)}$, двовимірний градієнт дорівнює ${\displaystyle {\vec {\nabla }}=({\frac {\partial }{\partial x}},{\frac {\partial }{\partial y}})}$, а вектор ${\displaystyle {\vec {\sigma }}}$ складається з матриць Паулі ${\displaystyle (\sigma _{1},\sigma _{2})}$. В матричній формі рівняння можна переписати наступним чином:

${\displaystyle {\begin{pmatrix}0&-i\hbar v{\frac {\partial }{\partial x}}-\hbar v{\frac {\partial }{\partial y}}+eBy\\-i\hbar v_{F}{\frac {\partial }{\partial x}}+\hbar v{\frac {\partial }{\partial y}}+eBy&0\end{pmatrix}}\psi (x,y)=\varepsilon \psi (x,y).}$

Тут можна легко розділити змінні й отримати в результаті спектр для релятивістських рівнів Ландау:

${\displaystyle \varepsilon _{n}=\pm \hbar \omega _{c}{\sqrt {n}}=\pm {\sqrt {\hbar v_{F}^{2}eB2n/c}},}$

де n = 0, 1, 2, …; ${\displaystyle {\tilde {\omega }}_{c}={\sqrt {2}}{\frac {v_{F}}{l_{B}}}}$ — циклотронна частота, ${\displaystyle l_{B}={\sqrt {\frac {\hbar c}{eB}}}}$ — магнітна довжина.

Вперше незвичайний (англ. unconventional) квантовий ефект Холла спостерігали в працях[3][4], де було показано, що носії заряду в графені дійсно мають «нульову» ефективну масу, оскільки положення плато на залежності недіагональної компоненти тензора провідності відповідали напівцілим значенням холлівської провідності ${\displaystyle \nu =\pm (|n|+1/2)}$ в одиницях ${\displaystyle 4e^{2}/h}$ (множник 4 відповідає чотирикратному виродженню по енергії), тобто

${\displaystyle \sigma _{xy}=\pm {\frac {4e^{2}}{h}}\left(|n|+{\frac {1}{2}}\right).}$

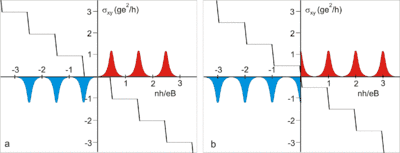
Це квантування сумісне з теорією квантового ефекту Холла для діраківських безмасових ферміонів[1]. Порівняння цілочисленного квантового ефекту Холла в звичайній двовимірній системі та графені показане на малюнку 1. Тут показані розширені рівні Ландау для електронів (виділене червоним кольором) та для дірок (синій колір). Якщо рівень Фермі знаходиться між рівнями Ландау, то на залежності холлівської провідності ${\displaystyle \sigma _{xy}}$ спостерігається ряд плато. Ця залежність відрізняється від звичайних двовимірних систем (аналогом може слугувати двовимірний електронний газ в кремнії, котрий є дводолинним напівпровідником в площинах еквівалентних {100}, тобто також має чотирикратне виродження рівнів Ландау і холлівські плато спостерігаються при ${\displaystyle \nu =4|n|}$).

Квантовий ефект Холла (КЕХ) може бути використаний як еталон опору, оскільки чисельне значення плато в графені дорівнює ${\displaystyle h/2e^{2}}$ і має високу точність, хоч якість виготовлених приладів поступається високорухливому ДЕГ в GaAs і, відповідно, точності квантування. Перевага КЕХ у графені полягає в тому, що він спостерігається при кімнатній температурі[6] (в магнітних полях, сильніших за 20 Т). Основне обмеження на спостереження КЕХ при кімнатній температурі викликається не температурною розмазкою розподілу Фермі — Дірака, а розсіюванням носіїв заряду на домішках, що призводить до розширення самих рівнів Ландау.

Рис. 1. a) Квантовий ефект Холла в звичайній двовимірній системі. b) Квантовий ефект Холла в графені. ${\displaystyle g=g_{s}g_{v}=4}$ — виродження спектра

• Квантовий ефект Холла