Дистанційно-успадковуваний граф

Оригінальне визначення дистанційно-успадковуваного графу — це граф G, такий, що, якщо будь-які дві вершини u і v належать зв'язному породженому підграфу H графу G, то деякий найкоротший шлях, що з'єднує u і v в G, має бути в підграфі H, причому відстань між u і v в H має бути такою ж, як у G.

Дистанційно-успадковувані графи можна описати кількома іншими еквівалентними способами:[5]

• Це графи, в яких будь-який породжений шлях є найкоротшим.
• Це графи, в яких будь-який цикл довжини щонайменше п'ять має дві або більше діагоналей і в яких будь-який цикл довжини рівно п'ять має щонайменше одну пару діагоналей, що перетинаються.
• Це графи, в яких будь-який цикл довжини п'ять і більше має щонайменше одну пару діагоналей, що перетинаються.
• Це графи, в яких для будь-яких чотирьох вершин u, v, w і x щонайменше дві з трьох сум відстаней d(u,v)+d(w,x), d(u,w)+d(v,x) и d(u,x)+d(v,w) рівні.
• Це графи, в яких немає ізометричних підграфів будь-якого циклу довжини п'ять і більше або будь-якого з трьох інших графів: 5-циклу з однією хордою, 5-циклу з двома хордами, що не перетинаються і 6-циклу з хордою, що сполучає протилежні вершини.

Три операції, за допомогою яких можна побудувати будь-який дистанційно-успадковуваний граф

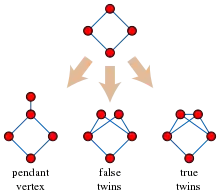
• Це графи, які можна створити з однієї вершини за допомогою послідовності трьох операцій (показаних на ілюстрації):
  1. Додавання нової висячої вершини, з'єднаної одним ребром з наявною вершиною графу.
  2. Заміна будь-якої вершини графу парою вершин, кожна з яких має тих самих сусідів, що й видалена вершина. Нова пара вершин називається двійнятами.
  3. Заміна будь-якої вершини графу парою вершин, кожна з яких має тих самих сусідів, що й видалена вершина, а також іншу вершину з пари. Нова пара вершин називається близнюками.
• Це графи, які можна повністю розкласти на кліки і зірки (повні двочасткові графи K_1,q) за допомогою розщеплювальної декомпозиції . У такому розщепленні отримують розклади графу на дві підмножини, такі, що розбивні ребра, які утворюють повний двочастковий підграф, формують два менших графи заміною кожного боку двочасткового графу вершинами з рекурсивним розщепленням цих двох підграфів[6].
• Це графи, які мають одиничну рангову ширину, де рангова ширина графу визначається як мінімум максимального рангу за всіма ієрархічними поділами вершин серед певних підматриць матриці суміжності графу, визначених поділом[7].

Будь-який дистанційно-успадковуваний граф є досконалим[2], точніше, цілком упорядковуваним графом[8]. Будь-який дистанційно-успадковуваний граф є також парним графом, графом, у якому будь-які два шляхи між однією і тією ж парою вершин мають одночасно або парну довжину, або непарну[9]. Будь-який парний степінь дистанційно-успадковуваного графу G (тобто граф G²ⁱ, утворений з'єднанням пар вершин на відстані, що не перевищує 2i в G) є хордальним графом[10].

Будь-який дистанційно-успадковуваний граф можна подати як граф перетинів хорд у колі, тобто як коловий граф. Це можна показати, побудувавши граф за допомогою додавання висячих вершин, «двійнят» і «близнюків», формуючи при цьому на кожному кроці набір хорд, що утворює граф. Додавання висячої вершини відповідає додаванню хорди поруч з кінцем наявною хорди так, що нова хорда буде перетинати тільки цю хорду. Додавання «двійнят» відповідає заміні хорди двома паралельними хордами, що перетинають один і той самий набір хорд. Додавання «близнюків» відповідає заміні хорди двома майже паралельними перетинними хордами, які перетинають один і той самий набір інших хорд.

Дистанційно-успадковуваний граф є двочастковим тоді і тільки тоді, коли в ньому немає трикутників. Двочастковий дистанційно-успадковуваний граф можна побудувати з єдиної вершини додаванням тільки висячих вершин і «двійнят», оскільки будь-які «близнюки» утворюють трикутник, а операції додавання висячої вершини і «двійнят» зберігають двочастковість.

Графи, які можна побудувати з єдиної вершини додаванням висячих вершин і створенням «близнюків» без операції створення «двійнят», є окремими випадками птолемеєвих графів і включають блокові графи. Графи, які можна створити з єдиної вершини створенням «двійнят» і «близнюків», але без додавання висячих вершин, — це кографи, які є, таким чином, дистанційно-успадковуваними. Кографи — це точно незв'язне об'єднання дистанційно-успадковуваних графів з діаметром 2. Окіл будь-якої вершини дистанційно-успадковуваного графу є кографом. Транзитивне замикання орієнтованого графу, утвореного вибором будь-якого набору орієнтацій ребер будь-якого дерева, є дистанційно-успадковуваним. Окремий випадок, у якому дерево орієнтоване в напрямі від деякої вершини, утворює підклас дистанційно-успадковуваних графів, відомий як тривіально досконалі графи, який також називають хордальними кографами[11].

Дистанційно-успадковувані графи можна розпізнати й розкласти на послідовність висячих вершин і операцій подвоєння за лінійний час[12].

Оскільки дистанційно-успадковувані графи досконалі, деякі оптимізаційні задачі можна розв'язати за поліноміальний час, хоча ці задачі NP-складні для загальніших класів графів. Отже, можна за поліноміальний час знайти максимальну кліку або незалежну множину в дистанційно-успадковуваному графі або знайти його оптимальне розфарбування[13]. Оскільки дистанційно-успадковувані графи є коловими графами, вони успадковують алгоритми з поліноміальним часом для колових графів. Наприклад, можна визначити за поліноміальний час деревну ширину будь-якого колового графу, а отже й будь-якого дистанційно-успадковуваного графу[14][15]. Крім того, клікова ширина будь-якого дистанційно-успадковуваного графу не перевищує трьох[16]. Як наслідок, за теоремою Курселя, для багатьох задач на цих графах існують ефективні алгоритми на основі динамічного програмування[17][18].

Деякі інші задачі оптимізації на дистанційно-успадковуваних графах можна розв'язати ефективно за допомогою алгоритмів, спеціально розроблених для таких графів. Як показали де Атрі та Москаріні[19], мінімальна зв'язна домінівна множина (або, еквівалентно, кістяк із максимально можливим числом листків) на дистанційно-успадковуваних графах можна знайти за поліноміальний час. Гамільтонів граф або гамільтонів шлях будь-якого дистанційно-успадковуваного графу можна знайти за поліноміальний час[20][21].

• Distance-hereditary graphs. Information System on Graph Classes and their Inclusions.