Граф порівнянності

Діаграма Гассе частково впорядкованої множини (зліва) і її граф порівнянності (праворуч)

Один із заборонених породжених підграфів графу порівнянності. Узагальнений цикл a-b-d-f-d-c-e-c-b-a в цьому графі має непарну довжину (дев'ять), але не має хорд тріангуляризації

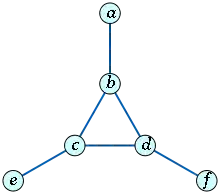
Для будь-якої частково строго впорядкованої множини (S, <) граф порівнянності (S, <) — це граф (S, ⊥), вершини якого — елементи S, а ребра — це пари {u, v} елементів, таких що u < v. Таким чином, для частково впорядкованих множин беремо орієнтований ациклічний граф, використовуємо транзитивне замикання і видаляємо орієнтацію.

Також, граф порівнянності — це граф, який має транзитивну орієнтацію[2], тобто орієнтація його ребер така, що відношення суміжності є транзитивним — якщо існують дуги (x, y) і (y, z), повинна існувати дуга (x, z).

Можна подати частково впорядковану множину, як сімейство множин таких, що x < y у частковому порядку, якщо відповідна x множина є підмножиною множини, відповідної y. Таким чином, можна показати, що граф порівнянності еквівалентний графу вкладеності сімейства множин, тобто графу, вершинами якого є множини сімейства, а ребра з'єднують вершини, якщо одна з множин міститься в іншій[3].

Також[4] граф порівнянності — це граф, у якому для будь-якого узагальненого циклу непарної довжини можна знайти ребро (x, y), яке з'єднує дві вершини, розташовані на відстані два в циклі. Такі ребра називають хордами тріангуляції. У цьому контексті узагальнені цикли є замкнутим обходом, який проходить кожне ребро графу не більше одного разу в кожному напрямку.

Граф порівнянності можна описати також заданням заборонених підграфів[5].

Будь-який повний граф є графом порівнянностілінійно впорядкованої множини. Всі ациклічні орієнтації в повному графі транзитивні. Будь-який двочастковий граф також є графом порівнянності. Орієнтація ребер двочаткового графу з одного боку в інший приводить до транзитивної орієнтації, що відповідає частковому порядку висотою два. Як зауважив Сеймур (Seymour, 2006), будь-який граф порівнянності, який не є ні повним, ні двочастковим, має косий розклад.

Доповнення будь-якого інтервального графу є графом порівнянності. Інтервальні графи — це точно хордальні графи, які мають доповненнями графи порівнянності[6].

Граф перестановки — це граф вкладеності множини інтервалів[7]. Таким чином, графи перестановок — це ще один клас графів порівнянності.

Тривіально досконалі графи — це графи порівнянності кореневих дерев[8]. Кографи можна схарактеризувати як графи порівнянності паралельно-послідовних часткових порядків. Отже, кографи теж є графами порівнянності[9].

Будь-який граф порівнянності є досконалим. Досконалість графів порівнянності стверджує теорема Мирського, а досконалість їх доповнень — теорема Ділуорса. Ці факти, разом зі властивістю подвійності досконалих графів, можна використовувати для доведення теореми Ділуорса з теореми Мирського і навпаки[10]. Точніше, графи порівнянності є цілком упорядковуваними графами, останні є підкласом досконалих графів — алгоритм жадібного розфарбовування для топологічного сортування транзитивної орієнтації графу розфарбовує його оптимально[11].

Доповнення будь-якого графу порівнянності є струнним графом[12].

Транзитивну орієнтацію графу, якщо вона існує, можна знайти за лінійний час[13]. Однак алгоритм, який це робить, визначає орієнтацію для будь-якого графу, так що для завершення задачі перевірки, чи є граф графом порівнянності, потрібно перевірити, чи є орієнтація транзитивною, що за складністю еквівалентне множенню матриць.

Оскільки графи порівнянності досконалі, багато задач, складні для загальніших класів графів, зокрема розфарбовування графів і задача про незалежну множину, для графів порівнянності можна розв'язати за поліноміальний час.

• Тривіально досконалий граф