Контрапозиція

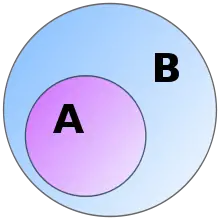
Згідно з колами Ейлера, що показані нижче, видно, що якщо щось входить у поняття А, то воно входить і в поняття B. Отже, цю діаграму можна тлумачити, як «усе, що входить до А — входить до B», тобто:

${\displaystyle A\to B}$

Також очевидно, що усе, що не входить до B (поза синім колом), не може належати до А. Наступне твердження —

${\displaystyle \neg B\to \neg A}$

— Є протиставленням. Можна підсумувати, що ${\displaystyle (A\to B)\to (\neg B\to \neg A)}$.

Це правило значно полегшує можливість щось довести у суперечках. Наприклад, якщо ми хочемо довести, що кожна дівчина у США (А) — білявка (B), ми можемо спробувати безпосередньо довести, що , ${\displaystyle A\to B}$ перевіряючи усіх дівчат США, чи мають вони біляве волосся. З іншого боку, ми можемо довести, що  ${\displaystyle \neg B\to \neg A}$ , перевіряючи дівчат з іншим кольором волосся, щоб побачити, чи правда, що всі вони поза США. Це означає, що, якщо ми знайдемо хоча б одну не білявку у США, це спростує вираз ${\displaystyle \neg B\to \neg A}$, а отже, й ${\displaystyle A\to B}$.

Отже, для кожного твердження, де А належить до B, є твердження, де все, що не належить до B, — не належить до А. Якщо ми підтвердимо або спростуємо одне з цих тверджень, то інше підтвердиться або спростовується автоматично. Вони абсолютно еквівалентні.

Твердження Q пов'язано із твердженням Р, коли їх відношення має такий вигляд:

${\displaystyle (P\to Q)}$

Прикладом виразу: «Якщо щось — Р, то воно Q» може бути вираз: «Якщо Сократ — чоловік, то він людина». При таких умовах, Р виступає антецедентом, а Q — консеквентом. Одне твердження — це протиставлення іншому тільки тоді, коли його антецедент заперечує консеквент іншого, і навпаки. Протиставлення як приклад:

${\displaystyle (\neg Q\to \neg P)}$.

Це означає, що «Якщо щось не є Q, то воно й не Р», або, користуючись попереднім прикладом, «Якщо Сократ не чоловік, то він не може бути людиною». Це судження протиставляється оригінальному, але воно є його логічним еквівалентом. Згідно з їх логічної еквівалентності, перше твердження підтверджує інше: якщо одне з них істинне, то інше — теж. Те ж саме відбувається, якщо вони хибні.

Строго кажучи, контрапозиція існує тільки при двох простих умовах. Але все ж контрапозиція може існувати при двох складних умовах, якщо вони подібні одна одній. Таким чином, твердження ${\displaystyle \forall {x}(P{x}\to Q{x})}$ — або «усі Ps належать до Qs» — протиставляється твердженню ${\displaystyle \forall {x}(\neg Q{x}\to \neg P{x})}$ — або «усе, що не входить до Qs — не належить до Ps».

Нехай :${\displaystyle (A\to B)\land \neg B}$. За умовою твердження, якщо А — істинне, то істинне й В, але, також, за умовами, В — хибне. Отже, стає очевидним, що А є хибним через суперечливість. Якби А було істинним, то В теж мало бути істинним. Проте, нам вказали, що В — хибне, тож у твердженні є протиріччя. Це означає, що А не є істинним (припускаючи, що ми маємо справу з конкретними твердженнями, що можуть бути або істинними, або хибними): ${\displaystyle (A\to B)\to (\neg B\to \neg A)}$ Такий самий процес ми можемо вживати й іншим чином: ${\displaystyle (\neg B\to \neg A)\land A}$. Відомо, що В або істинне, або хибне. Якщо В хибне, то хибне й А. Але, за умовою, А — істинне, а отже, припущення, що В є хибне, — суперечливість і не може бути істиною. Тобто, В має бути істинним:

${\displaystyle (\neg B\to \neg A)\to (A\to B)}$

Поєднуючи ці два доведених твердження, ми одержуємо їх логічний еквівалент:

${\displaystyle (A\to B)\iff (\neg B\to \neg A)}$

Логічна еквівалентність між двома твердженнями означає, що вони разом або істинні, або хибні. Щоб довести, що два протиставлення є логічно еквівалентними, треба розуміти, коли логічна імплікація є істинною, а коли — хибною.

${\displaystyle (P\to Q)}$

Р тільки тоді хибне, коли хибне Q. Отже, ми можемо скоротити твердження до «Вираз хибний, коли Р не належить до Q».

${\displaystyle \neg (P\land \neg Q)}$

Елементи кон'юнкції можуть бути протилежно сформульовані без змістових змін (за принципом комутативності):

${\displaystyle \neg (\neg Q\land P)}$

Ми визначаємо, що ${\displaystyle R}$ еквівалентне «${\displaystyle \neg Q}$», а ${\displaystyle S}$ — еквівалентне ${\displaystyle \neg P}$ (що означає, що ${\displaystyle \neg S}$ еквівалентне ${\displaystyle \neg \neg P}$, яке, в свою чергу, еквівалентне ${\displaystyle P}$)

${\displaystyle \neg (R\land \neg S)}$

Згідно із записом, не буде випадку, коли R — істинне, а S — хибне водночас, і це є визначенням логічної імплікації. Ми можемо здійснити таку заміну:

${\displaystyle (R\to S)}$

Коли ми міняємо наші визначення R та S, ми робимо наступний висновок:

${\displaystyle (\neg Q\to \neg P)}$

Візьмемо ствердження «Усі червоні об'єкти мають колір». Це можна еквівалентно сформулювати: «Якщо об'єкт червоний, отже, він має колір».

У протиставленні це виражається наступним: «Усі об'єкти, що не мають кольору, не є червоними». Це логічно випливає з нашого оригінального ствердження, і, що очевидно, цей вираз істинний.

У інверсії — «Якщо об'єкт не червоний, то кольору він не має». Наприклад, синій об'єкт — не червоний, але колір все ж таки має. Отже, інверсія хибна.

У конверсії — «Якщо об'єкт має колір, то він червоний». Звісно, що об'єкти бувають і інших кольорів, отже, конверсія хибна.

У запереченні — «Існує хоча б один червоний об'єкт, що не має кольору». Судження хибне, бо його спростовує оригінальне істинне ствердження.

Простіше кажучи, протиставлення є логічно еквівалентне даним умовним твердженням, хоча його недостатньо для самої логічної еквівалентності.

Візьмемо за тим самим прикладом ствердження, що «Усі чотирикутники мають чотири сторони», або, йому еквівалентне, «Якщо багатокутник — чотирикутник, то в нього чотири сторони».

У протиставленні: «Якщо у багатокутника не чотири сторони, то це не чотирикутник». Це логічно випливає і, як правило, протиставлення відповідає істині, як і оригінальне ствердження.

У інверсії: «Якщо багатокутник — не чотирикутник, у нього не чотири сторони». У цьому випадку, на відміну від попереднього, інверсія істинна.

У конверсії: «Якщо багатокутник має чотири сторони, то він — чотирикутник». І знов, на відміну від попереднього прикладу, конверсія істинна.

У запереченні: «Є хоча б один чотирикутник, у якому не чотири сторони». Зрозуміло, що це припущення хибне.

Якщо і ствердження, і конверсія є істинними, то їх називають логічно еквівалентними, і як приклад можна привести вираз: «Багатокутник є чотирикутником тільки тоді, коли в нього чотири сторони». Отже, якщо у багатокутника чотири сторони, то це чотирикутник, і, у той самий час, якщо це чотирикутник, то в нього обов'язково чотири сторони.

Якщо ствердження істинне, то його протиставлення теж істинне (і навпаки).

Якщо ствердження хибне, то його протиставлення теж хибне (і навпаки).

Якщо інверсія ствердження істинна, то його конверсія істинна (і навпаки).

Якщо інверсія ствердження хибна, то його конверсія хибна (і навпаки).

Якщо заперечення ствердження хибне, то ствердження істинне (і навпаки).

Якщо ствердження (або його протиставлення) та інверсія (або конверсія) обидва істинні або хибні водночас, то це логічна еквівалентність.

Через те, що протиставлення ствердження завжди має логічне значення (істинності або хибності) у самому ствердженні, це можна використовувати як сильний метод доказу математичних теорем. Доказ із контрапозицією (протиставленням) — це прямий доказ протиставлення ствердження. Але непрямі методи, як доказ протиріччям, теж можуть використовуватися з контрапозцією, як, наприклад, доказ ірраціональності квадратного кореня з двох. За визначенням раціонального числа, ствердження може бути побудовано як «якщо ${\displaystyle {\sqrt {2}}}$ — раціональне число, то воно може бути вираженим як нескоротний дріб». Це ствердження істинне, тому що просто є іншим формулюванням визначення. Протиставлення цього ствердження: «Якщо ${\displaystyle {\sqrt {2}}}$ не може бути вираженим як нескоротній дріб, то це число не раціональне». Протиставлення, як і оригінальне твердження, істинне. Отже, якщо можна довести, що ${\displaystyle {\sqrt {2}}}$ можна виразити як нескоротній дріб, то повинен бути випадок, коли ${\displaystyle {\sqrt {2}}}$ — не раціональне число. Останнє припущення можна підтвердити через суперечливість.

Попередній приклад використовував протиставлення визначення, щоб довести теорему. Можна також підтвердити теорему, довівши протиставлення ствердження цієї теореми. Щоб довести, що «якщо позитивне ціле число N — неквадратне число, його квадратний корінь є ірраціональним», ми можемо еквівалентно довести його протиставлення, що «якщо позитивне ціле число N має раціональний квадратний корінь, то N — квадратне число». Це можна показати, визначивши √N рівним раціональному виразові a/b, де a та b є додатними цілими числами без спільних множників, і їх піднесенням до квадрату, щоб здобути N = a²/b², і зауваживши, що (оскільки N — позитивне ціле число) b = 1, то N = a² — квадратне число.

• Числення висловлень
• Дедукція