Дедукція
Деду́кція (лат. deductio, від deduco — «низводжу, відводжу») — процес виведення висновку, що гарантовано слідує, якщо вихідні припущення істинні, то висновок на їх підставі є чинним (див. правильність). Висновок повинен базуватись винятково на основі попередньо наведених доказів та не повинен містити нової інформації про предмет, що досліджується. Дедукція була вперше описана у працях давньогрецьких філософів, таких як Арістотель.[1]Процес виведення дедуктивно правильний тоді і лише тоді, коли з точки зору логіки за умови істинності вихідних припущень висновки також істинні; або, логічно неможливі хибні висновки за правильних припущень.[2]
Дедуктивний, (англ. deductive, нім. deduktiv) — заснований на дедукції; дедуктивний метод — спосіб дослідження, при якому окремі положення логічно виводяться із загальних положень (аксіом, постулатів, законів).
У логіці використовуються два загальних методи отримання висновків: дедукція та індукція. Головною відмінністю індукції є те що для її застосування не вимагається знати усі факти до того як зробити висновок. Оскільки на практиці неможливо все з'ясувати перед тим як робити умовивід, дедукція не має широкого застосування у реальному світі, окрім математики й природничих наук, які використовують математичні методи. Індукція, натомість, оперує набором неповних фактів, та на їх основі робить висновок який напевно випливає, не даючи жодних гарантій щодо його істинності. Попри це, індукція дає можливість набувати нових знань, котрі не є очевидними при розгляді вихідних тверджень.
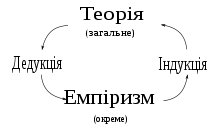
Часто зустрічається помилкова думка, що дедукція рухається від загального до окремого та що індукція — це рух у зворотному напрямку.
Дедукційна система
Нехай — множина формул, а — одна формула формальної мови. Дедукційна система може складатись з переліку аксіом та правил висновування. Твердження формальною мовою дедуктивно правильне, якщо існує послідовність формул в формальній мові, що завершується , така, що кожен член послідовності є або елементом з , аксіомою з , або виводиться з попередніх формул послідовності через правило висновування . Якщо правильне в , то записують , або просто .[2]
Визначення за Бетом
Нехай — вислів. Позначимо через твердження « не правильне», а через — твердження « правильне». Нехай
- — скінченна або нескінченна послідовність висловів. Вислів називається дедуктивно виводимим за Бетом із висловів , якщо існує семантична таблиця з протиріччям, побудована таким чином:[3]
- Крок 0. Розміщуємо в корінь.
- Крок . Приєднуємо в кінець кожної гілки без протиріч.
- Крок . Застосовуємо правила розширення до семантичної таблиці попереднього кроку .
Якщо послідовність висловів нескінченна, то така побудова може ніколи не завершитись. Вислів дедуктивно виводимий за Бетом тоді і лише тоді, якщо побудова завершується, і в результаті отримується семантична таблиця з протиріччям.
Якщо вислів дедуктивно виводимий за Бетом із висловів , то є логічним наслідком висловів . Формально це записується:[3]
Якщо вислів є логічним наслідком висловів , то логічно виводиться за Бетом із висловів . Формально це записується:
Примітки
- «Філософський словник» / За ред. В. І. Шинкарука. — 2.вид., перероб. і доп. — К.: Голов. Ред. УРЕ, 1986.
- Jacquette, Dale (2002). A companion to philosophical logic. Malden, Mass.: Blackwell. ISBN 0-631-21671-5.
- (Метакидес, 1998; с. 63)
Див. також
Література
- Філософський словник / за ред. В. І. Шинкарука. — 2-ге вид., перероб. і доп. — К. : Головна ред. УРЕ, 1986.
Посилання
- Дедукція // Юридична енциклопедія : [у 6 т.] / ред. кол.: Ю. С. Шемшученко (відп. ред.) [та ін.]. — К. : Українська енциклопедія ім. М. П. Бажана, 1998. — Т. 2 : Д — Й. — 744 с. — ISBN 966-7492-00-8.
- Індукція і дедукція // Українська мала енциклопедія : 16 кн. : у 8 т. / проф. Є. Онацький. — Накладом Адміністратури УАПЦ в Аргентині. — Буенос-Айрес, 1959. — Т. 2, кн. 4 : Літери Ж — Й. — С. 541. — 1000 екз.
- Дедукція // Літературознавча енциклопедія : у 2 т. / авт.-уклад. Ю. І. Ковалів. — Київ : ВЦ «Академія», 2007. — А — Л. — С. 260.
- Дедукція // Універсальний словник-енциклопедія. — 4-те вид. — К. : Тека, 2006.
- Г. Метакидес, А. Нероуд (1998). Принципы Логики и Логического Программирования. Факториал. ISBN 5-88688-037-2.